囲碁と似ているが、以下のような違いがある
すでにいくつかプログラムがあるので、プログラムを作られた方はお送りくだされば、こちらで対戦させることができます。
2人で行うボードゲームである(4人で行うルールもある)。9×9の盤の自分側の辺の中央に自分の駒を置いて始め、先にゴール(相手側の辺のどこか)に着いたほうが勝ちである。2人で交互に、駒を1マス進めるか、長さ2の壁をマスの境界に置く。壁はそれぞれが10枚ずつ持っている。
日本での実物の入手は簡単ではないが、ARiAdoNEというフリーソフトがある(ルール説明も含まれている)ので、遊んでみることができる。
昨年のコンピュータオリンピアード(ICGA トーナメント)に参加した人によると、壁を置くことにより最短経路が大きく変化するゲームであり、まだ人間のほうが強いということである。
プログラムを作られた方はお知らせください。
数独はペンシルパズルの一つで、9×9の正方形に並んだマスに1から9までの数字を入れて、各行、各列、各3×3のブロックに、各数字が1回ずつ現れるようにするものである(「数独(Sudoku)」のニコリ公式パズルガイド)。「数独」はニコリの登録商標なので、「ナンバープレース(ナンプレ)」と呼ばれることも多い。
数独には試行錯誤が不要という暗黙のルールがあるが、試行錯誤とは何かは議論の元となるため、ここでは解が一つだけであればよいとしておく。
25×25の数独についての報告(2012-8-19追加)
2005年の問題の最小公倍図形と同じである。当時は解がもっと小さい問題しか計算できなかった。
図形Aがいくつかの図形Bでできているとき「図形Aは図形Bで割りきれる」と定義します。ここで、図形としては単位正方形からなるもののみを考えています。
注意: 図形の演算を定義したわけではありません。
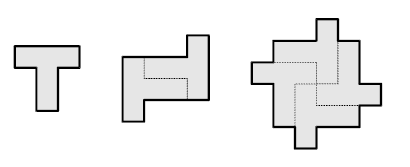
Tペントミノで割りきれる図形の例:
Oテトロミノ(4単位の正方形)で割りきれる図形の例: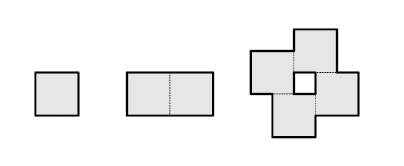
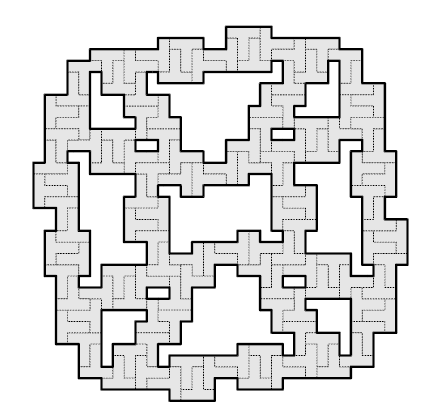
TペントミノとOテトロミノの両方で割りきれるなるべく小さい図形を見つけてください。(Robert Wainright氏による問題)[2011-12-2解答あり]
現在見つかっている最小の図形は以下のTペントミノ120個=Oテトロミノ150個(600単位)のものです(河原哲郎氏による)。初出時には「Tペントミノ150個(750単位)」としていましたが、訂正します(2011-2-27訂正追記)。
以下余白