数学アルゴリズム研究ノート (2)
2.非線形合同法による擬似乱数周期の延長
2003年7月 田沼英樹
2-1.非線形合同法の拡張
前回考察した二次合同法(あるいはさらに高次の合同法)は,線形合同法と同じく
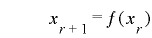
という形の一変数の漸化式を用いたものですが,この方式では基本的に周期が一変数のビット表現の組み合わせを超えることができず,また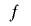 として多項式を用いているために,下位ビットの周期が短いという弱点も同様に受け継いでいます.
として多項式を用いているために,下位ビットの周期が短いという弱点も同様に受け継いでいます.
そこでまず,より長周期で優良な擬似乱数を得るために,多倍長演算でビット長を仮想的に増やす方法が考えられますが,多倍長の乗算は計算負荷が大きいため,これはあまり実用的であるとは言えません.
次に,二変数の漸化式
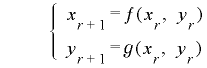
により周期を二変数の組み合わせに拡張することが考えられますが,まず単純に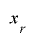 と
と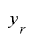 のビット長を
のビット長を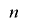 として,
として,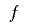 と
と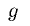 に多項式を用いて周期
に多項式を用いて周期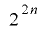 の擬似乱数を得ようとしても,これがどうにもうまくいきません.定理1-3の証明と同様の手法で延長した最上位ビットの挙動を調べようとしても,
の擬似乱数を得ようとしても,これがどうにもうまくいきません.定理1-3の証明と同様の手法で延長した最上位ビットの挙動を調べようとしても,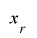 と
と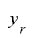 の組み合わせの周期が高次の
の組み合わせの周期が高次の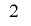 べきであるために,最上位ビットが反転しなくなってしまうのです.(確かめてみてください)
べきであるために,最上位ビットが反転しなくなってしまうのです.(確かめてみてください)
そこで,少し発想を変えて
![\left\{\begin{array}{l} {x_{r}} \text{は} \mathrm{[}1,2^{m}-1\mathrm{]} \text{の}曾mathrm{S}\text{ての}箪mathrm{l}\text{をとる}周期 2^{m}-1 \text{の}欺mathrm{[}似乱数\\ y_{r+1}=f(x_{r}, y_{r})\end{array}\right.](./random2_images/math013.png)
という形の擬似乱数を考えます.つまり,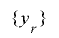 は種となる擬似乱数
は種となる擬似乱数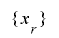 の周期を延長したものとなり,
の周期を延長したものとなり,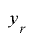 のビット長を
のビット長を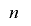 とすると,最大
とすると,最大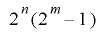 の周期をとり得ることになります.ここで,擬似乱数
の周期をとり得ることになります.ここで,擬似乱数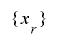 は条件として特殊な形の周期を持ちますが,多くのシフトレジスタ(あるいは有限体上の多項式環)をもとにした擬似乱数は,このような周期を持ちます.
は条件として特殊な形の周期を持ちますが,多くのシフトレジスタ(あるいは有限体上の多項式環)をもとにした擬似乱数は,このような周期を持ちます.
2-2.擬似乱数周期の延長
先に述べたように,まず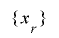 を
を![\mathrm{[}1, 2^{m}-1\mathrm{]}](./random2_images/math021.png) の全ての値をとるビット長
の全ての値をとるビット長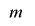 で周期
で周期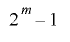 の擬似乱数列とし,
の擬似乱数列とし,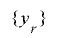 を合同式
を合同式
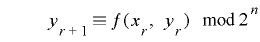
で生成されて![\mathrm{[}0, 2^{n}-1\mathrm{]}](./random2_images/math026.png) の値をとるビット長
の値をとるビット長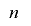 の数列とします.
の数列とします.
そして,関数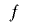 として二次式
として二次式
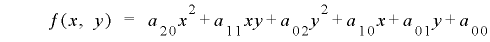
をとったときの値の組の列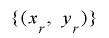 の周期について,定理1-3の証明と類似の手法で考察を行うことにします.
の周期について,定理1-3の証明と類似の手法で考察を行うことにします.
まず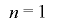 のとき,
のとき,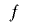 について
について
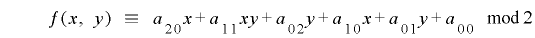
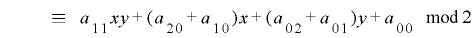
という合同式が成り立ちますが,簡単のために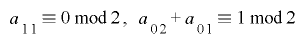 という制約条件を付け加えると
という制約条件を付け加えると
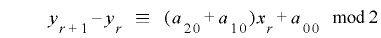
となり,![r\in\mathrm{[}0, 2^{m}-2\mathrm{]}](./random2_images/math037.png) について両辺の総和をとると
について両辺の総和をとると
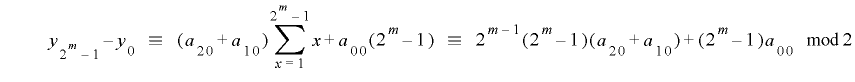
となることから,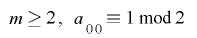 のとき
のとき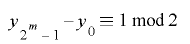 より
より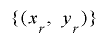 は周期
は周期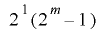 を持ちます.
を持ちます.
条件を一旦まとめると,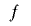 が
が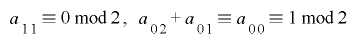 を満たすとき,
を満たすとき,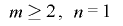 について
について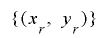 は周期
は周期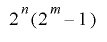 を持ちます.
を持ちます.
次に,ある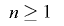 について
について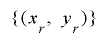 が周期
が周期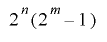 を持つと仮定し,
を持つと仮定し,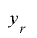 の上位に
の上位に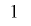 ビット拡張して
ビット拡張して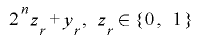 とおいて
とおいて
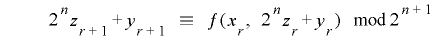
とした場合の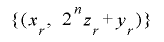 の周期を考えます.
の周期を考えます.
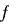 についての合同式
についての合同式
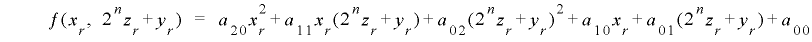
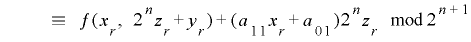
より,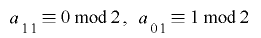 という制約条件を付け加えると
という制約条件を付け加えると
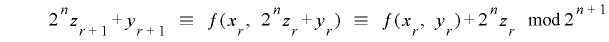
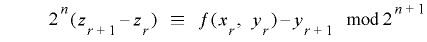
が成り立ちます.そこで![r\in\mathrm{[}0, 2^{n}(2^{m}-1)-1\mathrm{]}](./random2_images/math062.png) について両辺の総和をとると
について両辺の総和をとると
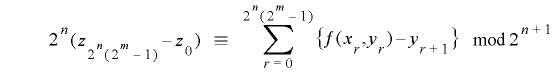
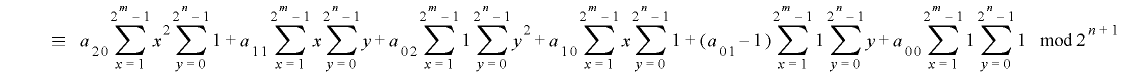
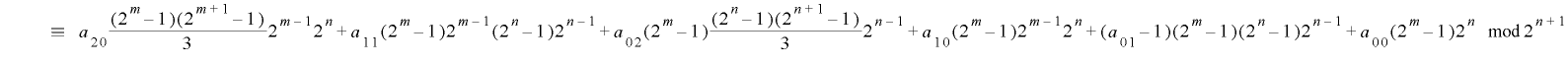
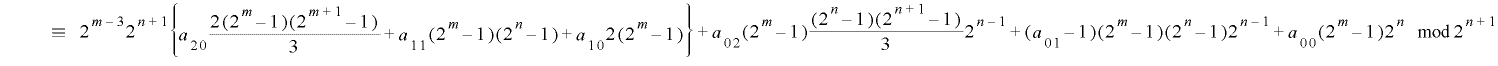
となることから,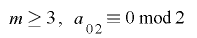 という制約条件を付け加えると
という制約条件を付け加えると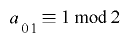 より
より
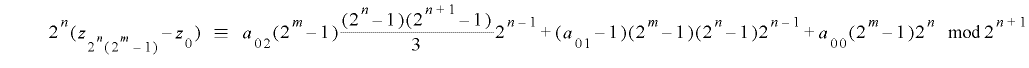
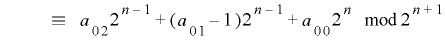
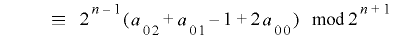 .
.
したがって,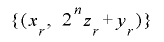 の周期が
の周期が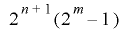 となるための条件は
となるための条件は
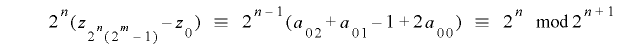
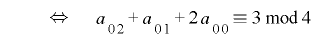
となり,前出の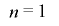 についての条件
についての条件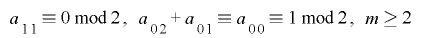 と合わせて
と合わせて
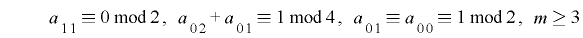
とすると,数学的帰納法により次の定理が成り立ちます.
【定理2-2-1】
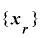 を
を![\mathrm{[}\bm{1}, \bm{2}^{\bm{m}}-\bm{1}\mathrm{]}](./random2_images/math080.png) の全ての値をとる周期
の全ての値をとる周期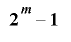 の整数列とし,
の整数列とし,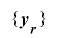 を
を![\mathrm{[}\bm{0}, \bm{2}^{\bm{n}}-\bm{1}\mathrm{]}](./random2_images/math083.png) の値をとる整数列で,整数係数の二次式
の値をとる整数列で,整数係数の二次式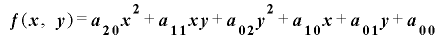 により合同式
により合同式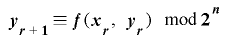 から生成されるものとする.このとき
から生成されるものとする.このとき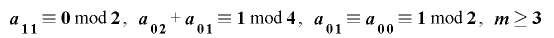 であるならば,任意の
であるならば,任意の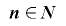 に対し値の組の列
に対し値の組の列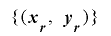 は周期
は周期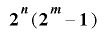 を持つ.
を持つ.
ここで一つ注意が必要なのは,値の組の列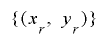 が最大周期を持ったとしても,数列
が最大周期を持ったとしても,数列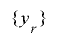 が必ずしも同じ周期を持つとは限らないということです.しかし,制約条件を少し増やすだけで,
が必ずしも同じ周期を持つとは限らないということです.しかし,制約条件を少し増やすだけで,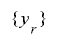 も同じ周期を持つことを示すことができます.
も同じ周期を持つことを示すことができます.
【系2-2-2】
定理2-2-1の条件に加え,さらに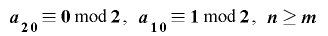 であるならば,
であるならば,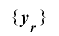 は周期
は周期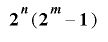 を持つ.
を持つ.
[証明]
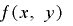 を
を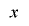 の多項式とみなすと定理1-2の条件を満たすことから,
の多項式とみなすと定理1-2の条件を満たすことから,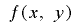 は変数
は変数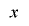 について単射である.
について単射である.
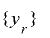 の周期を
の周期を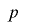 とおくと
とおくと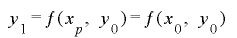 となるが,
となるが,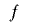 の単射性から
の単射性から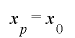 となり,
となり,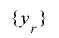 は
は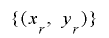 と同じ周期を持つ.■
と同じ周期を持つ.■
このように,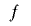 の単射性を仮定することによって容易に
の単射性を仮定することによって容易に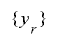 の最大周期が保証されるわけですが,このままでは
の最大周期が保証されるわけですが,このままでは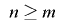 という条件があるために,
という条件があるために,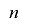 がワード長で制限されているときには周期が高々
がワード長で制限されているときには周期が高々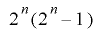 で頭打ちになってしまいます.
で頭打ちになってしまいます.
そこで,もう少し詳細な解析を行うことにより,次の様に条件を緩めることができます.
【系2-2-3】
定理2-2-1の条件に加え,さらに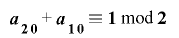 であるならば,
であるならば,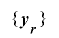 は周期
は周期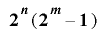 を持つ.
を持つ.
[証明]
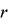 が
が![\mathrm{[}0, 2^{m}-2\mathrm{]}](./random2_images/math116.png) にわたって動くとしたとき,
にわたって動くとしたとき,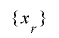 の最下位ビットが
の最下位ビットが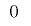 となる回数は
となる回数は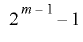 ,
,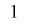 となる回数は
となる回数は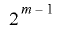 である.
である.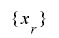 の最下位ビットの周期を
の最下位ビットの周期を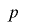 とし,周期内で最下位ビットが
とし,周期内で最下位ビットが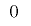 となる回数を
となる回数を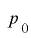 ,
,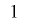 となる回数を
となる回数を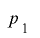 とすると
とすると
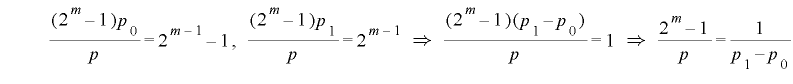
となるが,両辺は整数であることから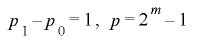 となり,
となり,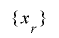 の最下位ビットの列は周期
の最下位ビットの列は周期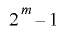 を持つ.
を持つ.
次に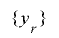 の周期を
の周期を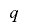 とおくと,任意の
とおくと,任意の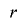 について
について
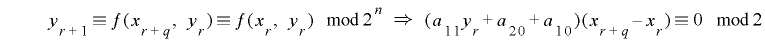
となることから,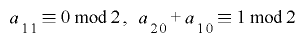 のとき
のとき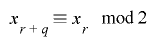 となり,
となり,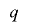 は
は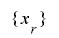 の最下位ビット列の周期
の最下位ビット列の周期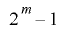 の倍数となる.
の倍数となる.
ここで,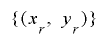 の周期
の周期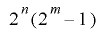 は
は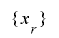 の周期
の周期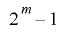 と
と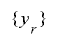 の周期
の周期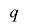 の最小公倍数であるが,
の最小公倍数であるが,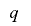 が
が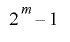 の倍数であることから
の倍数であることから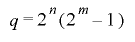 となり,
となり,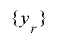 は周期
は周期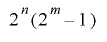 を持つ.■
を持つ.■
このように,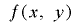 が
が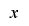 の最下位ビットについて単射であるという条件だけで
の最下位ビットについて単射であるという条件だけで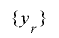 の周期が最大になることが保証されますが,実際に擬似乱数として利用する場合にはなるべく
の周期が最大になることが保証されますが,実際に擬似乱数として利用する場合にはなるべく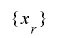 について多くの情報が反映されることが望ましく,下位
について多くの情報が反映されることが望ましく,下位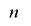 ビットについて単射であるための条件
ビットについて単射であるための条件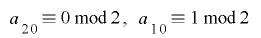 を満たしている方が良いものと思われます.
を満たしている方が良いものと思われます.
そこで,このような擬似乱数列の延長を以下のように定義します.
【定義2-2-4】
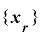 を周期
を周期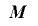 の整数列とし,
の整数列とし,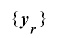 を
を![\mathrm{[}\bm{0}, \bm{2}^{\bm{n}}-\bm{1}\mathrm{]}](./random2_images/math161.png) の値をとる整数列で,関数
の値をとる整数列で,関数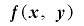 により合同式
により合同式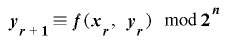 から生成されるものとする.このとき
から生成されるものとする.このとき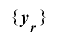 は
は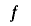 による
による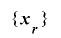 の延長であるという.ここで
の延長であるという.ここで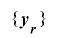 の周期が
の周期が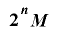 であるとき,この延長は全周期的であるという.また
であるとき,この延長は全周期的であるという.また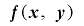 が
が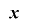 の下位
の下位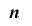 ビットについて単射であるならば,この延長は単射的であるという.
ビットについて単射であるならば,この延長は単射的であるという.
上記の定理および系は,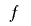 が二次式のときに擬似乱数列の延長が全周期的であるための十分条件を示していることになります.つまり,これらの結果をまとめて言い換えると,次の定理になります.
が二次式のときに擬似乱数列の延長が全周期的であるための十分条件を示していることになります.つまり,これらの結果をまとめて言い換えると,次の定理になります.
【定理2-2-5】
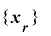 を
を![\mathrm{[}\bm{1}, \bm{2}^{\bm{m}}-\bm{1}\mathrm{]}](./random2_images/math174.png) の全ての値をとる周期
の全ての値をとる周期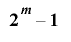 の整数列(ただし
の整数列(ただし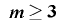 とする)とし,
とする)とし,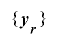 を整数係数の二次式
を整数係数の二次式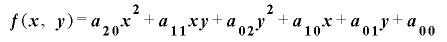 による
による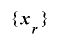 の延長とする.このとき
の延長とする.このとき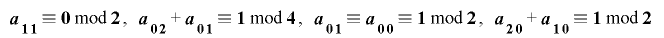 であるならば,この延長は全周期的である.また
であるならば,この延長は全周期的である.また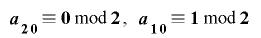 であるならば,この延長は単射的である.
であるならば,この延長は単射的である.
ここで,実用的には乗算を一度で済ませるために,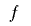 を一次式の積として表現した方が便利になります.
を一次式の積として表現した方が便利になります.
【系2-2-6】
定理2-2-5の条件のもとで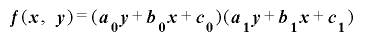 とおく.このとき
とおく.このとき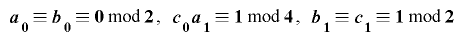 ならば
ならば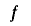 による延長は全周期的かつ単射的である.
による延長は全周期的かつ単射的である.
2-3.延長擬似乱数の性質
この擬似乱数の延長は,かき混ぜ法(前回の参考文献を参照)と同様に乱数の性質の改良を図るとともに,さらに乱数周期の延長までできるということから,かなり強力な乱数発生の手段となり得ます.そして非常に興味深いのは,全く性質の異なる二種類の擬似乱数を,ただ単に加えたりするのではなく,本質的に融合できるということです.
例えば,C言語表記で次のような変換から得られる数列を考えます.
x = (g &−(x&1)) ^ (x>>1)
ここで, g のところには何か適当な定数を置くことになりますが,例えば x を32ビットの符号なし整数とした場合, g に 0x80000057 を指定して 0 以外の値を x の初期値とすると,周期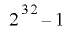 の数列が得られます.これは,原始多項式
の数列が得られます.これは,原始多項式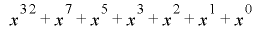 によって生成されるシフトレジスタによる乱数列に相当します.一般に,有限体上の多項式の演算を利用した数列は,整数の合同式とくらべて比較的容易に長い周期を得ることができます.
によって生成されるシフトレジスタによる乱数列に相当します.一般に,有限体上の多項式の演算を利用した数列は,整数の合同式とくらべて比較的容易に長い周期を得ることができます.
ところが,この数列は特定の1ビットのみを取り出して利用する分にはある程度乱数として有効なのですが,シフトレジスタ全体を整数値として取り出した場合,例えば偶数値の次は必ず半分の値になるといったように値の相関がかなり強く,そのままでは擬似乱数としてほとんど使い物になりません.そこで,この数列を元にして非線形合同法で延長することにより,相関を消した上でさらに長周期の擬似乱数を得ることが可能になります.(次回,詳しく検討します)
このように,有限体上の多項式環と整数の合同式という全く異質のものが融合して互いに補い合うというのは,それ自体数学的にも興味深いものであるといえます.
延長された擬似乱数列の性質については,その多くを種になる数列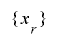 と変換関数
と変換関数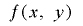 に依るために一般的にあまり細かなことは言えませんが,ほぼ自明な範囲で以下の定理が成り立ちます.
に依るために一般的にあまり細かなことは言えませんが,ほぼ自明な範囲で以下の定理が成り立ちます.
【定理2-3-1】
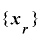 を
を![\mathrm{[}\bm{1}, \bm{2}^{\bm{m}}-\bm{1}\mathrm{]}](./random2_images/math191.png) の全ての値をとる周期
の全ての値をとる周期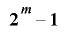 の整数列とし,
の整数列とし,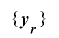 を
を![\mathrm{[}\bm{0}, \bm{2}^{\bm{n}}-\bm{1}\mathrm{]}](./random2_images/math194.png) の値をとる整数列で,
の値をとる整数列で,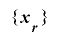 の全周期的かつ単射的な延長であるとする.もし
の全周期的かつ単射的な延長であるとする.もし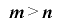 であるならば,隣接する2つの値の組
であるならば,隣接する2つの値の組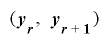 は
は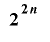 通りの全ての値の組み合わせをとる.また
通りの全ての値の組み合わせをとる.また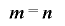 であるときは,
であるときは,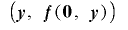 という形の組を除外した
という形の組を除外した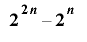 通りの値の組み合わせを周期内に一回ずつとる.
通りの値の組み合わせを周期内に一回ずつとる.
このように,種になる数列と変換関数についてあまり仮定することなく,2次元についての均等分布が保証されることになります.
さらに,種になる数列が多次元について均等に分布することがわかっている場合,次のことがいえます.
【定理2-3-2】
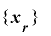 の隣接する
の隣接する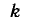 個の組
個の組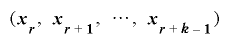 の下位
の下位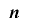 ビットの値が
ビットの値が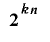 通りの全ての組み合わせをとり得るとき,その全周期的かつ単射的な延長である
通りの全ての組み合わせをとり得るとき,その全周期的かつ単射的な延長である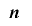 ビットの数列
ビットの数列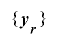 の
の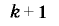 個の組
個の組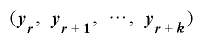 は
は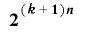 通りの全ての値の組み合わせをとる.
通りの全ての値の組み合わせをとる.
つまり,種になる数列が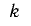 次元について均等に分布するとき,その全周期的かつ単射的な延長は
次元について均等に分布するとき,その全周期的かつ単射的な延長は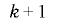 次元について均等に分布することがわかります.ただし,この多次元均等分布は
次元について均等に分布することがわかります.ただし,この多次元均等分布は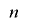 ビット全体についてのものであって,さらに上位ビットのみについてより多次元に均等分布するといった詳細な結果を得るためには,おそらく個々の変換関数
ビット全体についてのものであって,さらに上位ビットのみについてより多次元に均等分布するといった詳細な結果を得るためには,おそらく個々の変換関数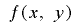 について詳しく解析を行う必要があります.
について詳しく解析を行う必要があります.
ここで,多次元均等分布が保証されている擬似乱数列で,先に述べた方法で延長可能なものの具体例として, Mersenne Twister [1] というものがあります.この擬似乱数生成法はシフトレジスタによる擬似乱数を究極にまで発展させた手法で,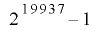 という非常に長い周期と,
という非常に長い周期と,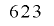 次元にわたって均等分布するという著しい性質を持ち,また高速に実行できるという特徴を持っています.この擬似乱数の出力は
次元にわたって均等分布するという著しい性質を持ち,また高速に実行できるという特徴を持っています.この擬似乱数の出力は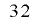 ビットの整数列となりますが,実際には
ビットの整数列となりますが,実際には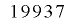 ビットの内部状態を持ち,その一部を変換して出力していることから,仮想的には
ビットの内部状態を持ち,その一部を変換して出力していることから,仮想的には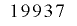 ビットの整数列の下位
ビットの整数列の下位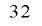 ビットのみを取り出して使っているとみなすことができます.したがって,定理2-2-5で非線形合同法により
ビットのみを取り出して使っているとみなすことができます.したがって,定理2-2-5で非線形合同法により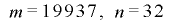 として周期を
として周期を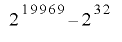 に延長することが可能となり,またそれが単射的であれば,定理2-3-2により
に延長することが可能となり,またそれが単射的であれば,定理2-3-2により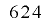 次元にわたって均等に分布することがわかります.ただし, Mersenne Twister には出力の上位ビットのみについても優れた多次元分布を持つといった性質がありますが,これについては延長によってかえって失われてしまう可能性があります.
次元にわたって均等に分布することがわかります.ただし, Mersenne Twister には出力の上位ビットのみについても優れた多次元分布を持つといった性質がありますが,これについては延長によってかえって失われてしまう可能性があります.
もっとも,実用的には Mersenne Twister をさらに延長する必要性などあまりないのかもしれませんが,理論的にはこういった別の方向からもさらに新しい発展の可能性があることを示しておきたいと思います.
参考リンク
[1] Mersenne Twister: A random number generator