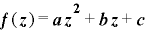 に対し,整数列
に対し,整数列 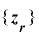 を
を 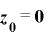 ,
,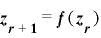 と定義する.
と定義する.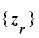 が任意の自然数
が任意の自然数 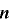 について
について 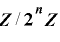 上で周期
上で周期 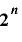 をもつための必要十分条件は,
をもつための必要十分条件は,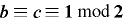 かつ
かつ 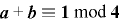 .
.【定理】
整数係数多項式 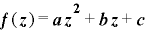 に対し,整数列
に対し,整数列 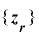 を
を 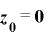 ,
,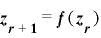 と定義する.
と定義する.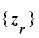 が任意の自然数
が任意の自然数 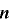 について
について 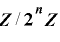 上で周期
上で周期 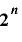 をもつための必要十分条件は,
をもつための必要十分条件は,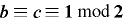 かつ
かつ 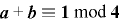 .
.
[補題1]
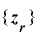 が
が 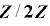 上で周期
上で周期 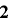 をもつための必要十分条件は,
をもつための必要十分条件は,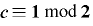 かつ
かつ 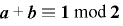 .
.
[補題1の証明]
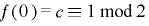 ,
,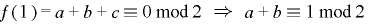 .
.
[補題2]
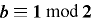 のとき,任意の
のとき,任意の 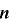 について
について 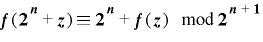 .逆に
.逆に 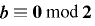 のとき,
のとき,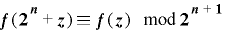 より
より 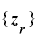 は
は 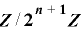 上で周期
上で周期 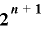 をもたない.
をもたない.
[補題2の証明]
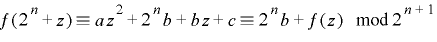 .
.
[補題3]
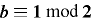 かつ
かつ 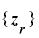 が
が 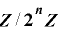 上で周期
上で周期 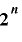 をもつとき,
をもつとき,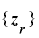 が
が 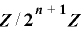 上で周期
上で周期 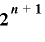 をもつための必要十分条件は
をもつための必要十分条件は
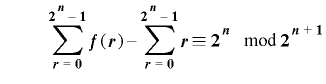 .
.
[補題3の証明]
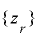 の
の 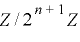 への射影を最上位ビット成分
への射影を最上位ビット成分 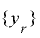 と下位
と下位 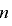 ビット成分
ビット成分 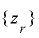 に分解し,
に分解し,
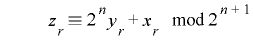 (
(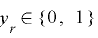 ,
,![x_{r}\in[0, 2^{n}-1]](./theorem1-3_images/math042.png) )
)
とする.補題2より
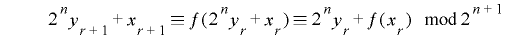 (以下
(以下 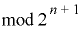 を省略)
を省略)
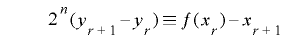 .
.
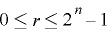 について両辺の総和をとると,
について両辺の総和をとると,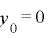 より
より
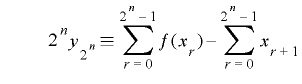 .
.
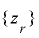 が
が 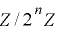 上で周期
上で周期 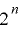 をもつことから,右辺の
をもつことから,右辺の 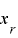 および
および 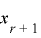 は
は ![[0, 2^{n}-1]](./theorem1-3_images/math054.png) の値を一度ずつとり,
の値を一度ずつとり,
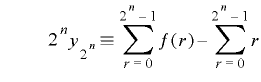 .
.
ここで,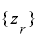 の
の 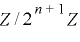 上の周期は
上の周期は 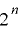 と
と 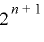 のいずれかであるが,
のいずれかであるが,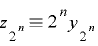 より周期が
より周期が 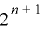 となるための必要十分条件は
となるための必要十分条件は 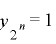 であり,これにより補題が証明される.
であり,これにより補題が証明される.
【定理の証明】
補題1および補題2より,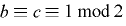 かつ
かつ 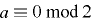 が定理の必要条件となる.この条件のもとで,ある
が定理の必要条件となる.この条件のもとで,ある 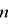 について
について 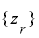 が
が 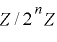 上で周期
上で周期 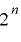 をもつと仮定する.(
をもつと仮定する.(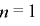 では成立)
では成立)
このとき補題3より,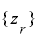 が
が 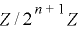 上で周期
上で周期 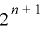 をもつための必要十分条件は
をもつための必要十分条件は
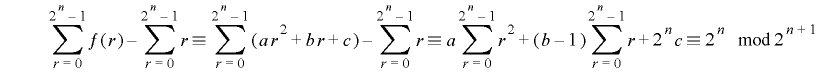
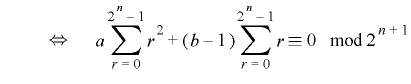
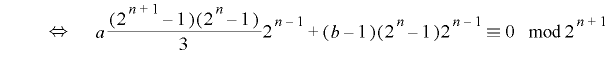
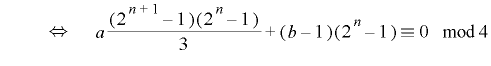
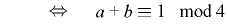 .
.
したがって,これらの条件をまとめて 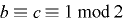 かつ
かつ 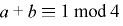 とすると,補題3および数学的帰納法により任意の自然数
とすると,補題3および数学的帰納法により任意の自然数 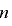 について
について 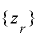 が
が 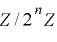 上で周期
上で周期 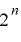 をもつ.■
をもつ.■