2020センター試験【数 学 $II$・数 学 B】
第1問 ( 必 答 問 題 ) ( 配 点 30)
[1]
(1) $0\leqq \theta <2\pi$ の と き
$\sin \theta >\sqrt{3}\cos(\theta-\frac{\pi}{2})\cdots
\require{enclose}\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}
$
と な る $\theta$ の 値 の 範 囲 を 求 め よ う 。
加 法 定 理 を 用 い る と
$\sqrt{3}\cos(\theta-\frac{\pi}{3})=\sqrt{3}\left(\cos \theta \cos \frac{\pi}{3}+\sin \theta \sin \frac{\pi}{3}\right)\\
=\sqrt{3}\left(\cos \theta \times \frac{1}{2}+\sin \theta \times \frac{\sqrt{3}}{2}\right)\\
=\frac{\sqrt{3}}{2}\cos \theta +\frac{3}{2}\sin \theta \ \ \left(\fbox{ア},\fbox{イ},\fbox{ウ}\right)$
である。よって、三角関数の合成を用いると$\require{enclose}\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}
$は
$\sqrt{3}\cos(\theta-\frac{\pi}{2})-\sin \theta \\
=\frac{\sqrt{3}}{2}\cos \theta +\frac{3}{2}\sin \theta-\sin \theta\\
=\frac{\sqrt{3}}{2}\cos \theta +\frac{1}{2}\sin \theta\\
=\sin \frac{\pi}{3}\cos \theta +\cos \frac{\pi}{3}\sin \theta\\
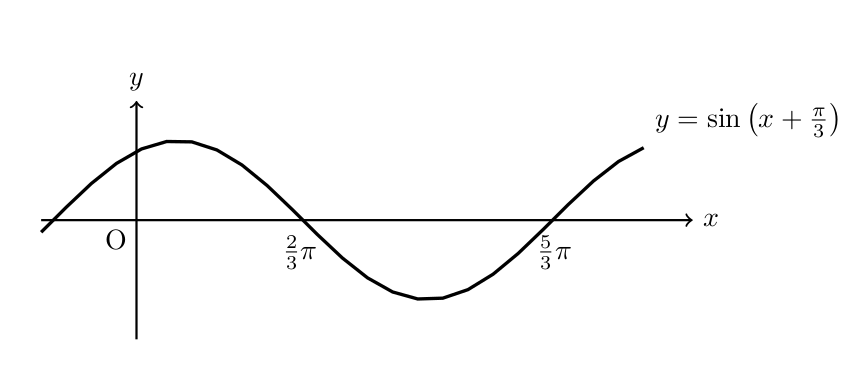
=\sin (\theta +\frac{\pi}{3})<0 \ \ \left(\fbox{エ}\right)
$
と変形できる。したがって、求める範囲は
$\theta+\frac{\pi}{3}=\pi,\theta+\frac{\pi}{3}=2\pi$を解いて
$\frac{2}{3}\pi <\theta <\frac{5}{3}\pi \ \ \left(\fbox{オ},\fbox{カ},\fbox{キ},\fbox{ク}\right)$
である。
(2) $0\leqq\theta\leqq \frac{\pi}{2}$と し ,$k$ を 実 数 と す る 。$\sin \theta$ と $\cos \theta$ は$x$ の2次方程式
$25x^2-35x+k=0$ の 解 で あ る と す る 。 こ の と き , 解 と 係 数 の 関 係 に よ
り
$\sin \theta+\cos \theta$ と $\sin \theta\cos \theta$ の 値 を 考 え れ ば ,
$\sin \theta+\cos \theta=\frac{35}{25}=\frac{7}{5},\sin \theta\cos \theta=\frac{k}{25}$
$\left(\frac{7}{5}\right)^2=(\sin \theta+\cos \theta)^2=\sin^2 \theta+\cos^2 \theta+2\sin \theta \cos \theta=1+2\times \frac{k}{25}$
つまり、$\frac{49}{25}-1=\frac{2k}{25}$
これを解いて $k=12\ \ \fbox{ケコ}$であることが
わ か る 。
さ ら に , $\theta$ が $\sin \theta\geqq \cos \theta$を満たすとすると,
$25x^2-35x+12=$より、$x=\frac{35\pm\sqrt{(-35)^2-4\times 25\times12}}{50}=\frac{35\pm 5}{50}=\frac{7\pm 1}{10}$だから、
$\sin \theta=\frac{4}{5} ,\cos \theta=\frac{3}{5}$
で あ る 。$ \ \ \left(\fbox{サ},\fbox{シ},\fbox{ス},\fbox{セ}\right)$
こ の と き , $\theta$ は
$
\frac{\pi}{4}\leqq \theta \leqq \frac{\pi}{3}\ \ (\ \require{enclose}\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 3\kern .06em}}\ )$ を 満たす。 $\left(\fbox{ソ}\right)
$
[2]
(1)$t$は正の実数であり、$t^{\frac{1}{3}}-t^{-\frac{1}{3}}=-3$を満たすとする。このとき
$(t^{\frac{1}{3}}-t^{-\frac{1}{3}})^2=t^{\frac{2}{3}}+t^{-\frac{2}{3}}-2t^{\frac{1}{3}}t^{-\frac{1}{3}}=9$だから
$t^{\frac{2}{3}}+t^{-\frac{2}{3}}=11\ \ \left(\fbox{タ},\fbox{チ}\right)$
さらに
$(t^{\frac{1}{3}}+t^{-\frac{1}{3}})^2=t^{\frac{2}{3}}+t^{-\frac{2}{3}}+2t^{\frac{1}{3}}t^{-\frac{1}{3}}=11+2=13$だから
$t^{\frac{1}{3}}+t^{-\frac{1}{3}}=\sqrt{13}\ \ \left(\fbox{ツ},\fbox{テ}\right)$
また
$(t^{\frac{1}{3}}-t^{-\frac{1}{3}})^3=t^{\frac{3}{3}}-3t^{\frac{2}{3}}t^{-\frac{1}{3}}+3t^{\frac{1}{3}}t^{-\frac{2}{3}}-t^{-\frac{3}{3}}\\
=t-t^{-1}-3(t^{\frac{1}{3}}-t^{-\frac{1}{3}})=t-t^{-1}+9=-27$
だから
$t-t^{-1}=-36\ \ \left(\fbox{ト},\fbox{ナ},\fbox{ニ}\right)$
である。
(2)$x,y$は正の実数とする。途立不等式
$
\left\{\begin{align}
\log_3 (x\sqrt{y})\leqq 5 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}\\
\log_{81} \frac{y}{x^3} \leqq 1 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 3\kern .06em}}
\end{align}\right.
$
について考える 。
$X=\log_3 x,Y=\log_3 Y$とおくと,$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}$は
$
\log_3 (x\sqrt{y})=\log_3 x+\frac{1}{2}\log_3 Y\leqq 5\\
2\log_3 x+\log_3 y\leqq 10
$
より
$2X十Y \leqq 10 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 4\kern .06em}}\ \ \left(\fbox{ヌ},\fbox{ネノ}\right)$
と変形でき,$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 3\kern .06em}}$は
$
\log_{81} \frac{y}{x^3} =\log_{81} y-\log_{81} x^3\\
=\frac{\log_3 y}{\log_3 81}-\frac{\log_3 x^3}{\log_3 81}\\
=\frac{\log_3 y}{\log_3 3^4}-\frac{\log_3 x^3}{\log_3 3^4}\\
=\frac{\log 3 y-3\log_3 x}{4}\leqq 1
$
より
$3X-Y\geqq -4 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 5\kern .06em}}\ \ \left(\fbox{ハ},\fbox{ヒフ}\right)$
と変形できる 。
$X,Y$が
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 4\kern .06em}}$
と
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 5\kern .06em}}
$を満たすとき , $Y$のとり得る最大の整数の値は
この不等式を解いてグラフを描けば
$7\ \ \left(\fbox{ヘ}\right)$
とわかる。また、$x,y$が$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}$と$\log_3 y=7$を同時に満たすととき、
$
2\log_3 x\leqq 10-7=3\\
\log_3 x \leqq \frac{3}{2}\\
x\leqq 3^{\frac{3}{2}}\\
x^2\leqq 3^3=27
$
だから、
$x$のとり得る最大の整数の値は$5\ \ \left(\fbox{ホ}\right)$である。
第2問 (必答問題) (配点30)
$a>0$とし,$f(x)=x^2-(4a-2)x+4a^2+1$とおく。座標平面上で,放物
線$y=x^2+2x+1$を$C$、放物線$y=f(x)$を$D$のとする。また,$\ell$を$C$と$D$の両
方に接する直線とする。
(1)$\ell$の方程式を求めよう。
$\ell$と$C$は点$(t,t^2+2t+1)$において接するとすると,$\ell$の方程式は
$y-(t^2+2t+1)=(2t+2)(x-t)$より
$y=(2t+2)x-2t^2-2t+t^2+2t+1$だから
$y=(2t+2)x-t^2+1 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}\ \ \left(\fbox{ア},\fbox{イ},\fbox{ウ}\right)$
である。また,$\ell$と$D$は点$(s,f(s))$において接するとすると,$\ell$の方程式は
$y-\{s^2-(4a-2)s+4a^2+1\}=(2s-4a+2)(x-s)$より
$y=(2s-4a+2)x-2s^2+4as-2s+s^2-4as+2s+4a^2+1$だから
$y=(2s-4a+2)x-s^2+4a^2+1 \cdots \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}\ \ \left(\fbox{エ},\fbox{オ},\fbox{カ},\fbox{キ},\fbox{ク}\right)$
である。ここで,$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$と$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}$は同じ直線を表しているので、
$2t+2=2s-4a+2\ ,\ -t^2+1=-s^2+4a^2+1$より
$
t=0\\
s=2a
\ \ \left(\fbox{ク},\fbox{ケ}\right)
$
が成り立つ。
したがって、$\ell$の方程式は$y=2x+1$である。$\ \ \left(\fbox{サ},\fbox{シ}\right)$
(2)二つの放物線$C,D$の交点の$x$座標$a$はである。$\ \ \left(\fbox{ス}\right)$
$C$と直線$\ell$および直線$x=a$で囲まれた図形の面積を$S$とすると、
$
S=\displaystyle{\int_{0}^{a} \{x^2+2x+1-(2x+1)\} dx=\int_{0}^{a} x^2 dx=\frac{a^3}{3}}$
である。$\ \ \left(\fbox{セ},\fbox{ソ}\right)$
(3)$a\geqq\frac{1}{2}$とする。二つの放物線$C,D$と直線$\ell$で囲まれた図形の中で
$0\leqq x \leqq 1$を満たす部分の面穂$T$は,$a>1\ \ \left(\fbox{タ}\right)$のとき,$a$の値によらず
$T=\displaystyle{\int_{0}^{1} x^2 dx=\frac{1}{3}} \ \ \left(\fbox{チ},\fbox{ツ}\right)$
であり、$\frac{1}{2}\leqq a \leqq 1$のとき
$
T=\displaystyle{\int_{0}^{a} x^2 dx+\int_{a}^{1} \{x^2-(4a-2)x+4a^2+1-(2x+1)}\}dx\\
=\displaystyle{\frac{a^3}{3}+\int_{a}^{1} (x^2-4ax+4a^2)}dx\\
=\displaystyle{\frac{a^3}{3}+ \left[ \frac{x^3}{3}-2ax^2+4a^2x \right]_{a}^{1}}\\
=\displaystyle{\frac{a^3}{3}+ \left[ \frac{1}{3}-2a+4a^2-\frac{a^3}{3}+2a^3-4a^3 \right]}\\
=\displaystyle{-2a^3+4a^2-2a+\frac{1}{3}} \ \ \left(\fbox{テ},\fbox{ト},\fbox{ナ},\fbox{ニ},\fbox{ヌ}\right)
$
である。
(4)次に、(2),(3)で定めた$S,T$に対して、$U=2T-3S$とおく。$a$が
$\frac{1}{2}\leqq a \leqq 1$の範囲を動くとき、
$U=-4a^3+8a^2-4a+\frac{2}{3}-a^3=-5a^3+8a^2-4a+\frac{2}{3}$
$U'=-15a^3+16a-4=-(3a-2)(5a-2)$より
$
\begin{array}{|c|c|c|c|c|c|}\hline
a&\cdots&\frac{2}{5}&\cdots&\frac{2}{3}&\cdots \\ \hline
U'&-&0&+&0&- \\ \hline
U&\searrow&&\nearrow&\frac{2}{27}&\searrow \\ \hline
\end{array}
$
だから
$U$は$a=\frac{2}{3} \ \ \left(\fbox{ネ},\fbox{ノ}\right)$で最大値$\frac{2}{27} \ \ \left(\fbox{ハ},\fbox{ヒ},\fbox{フ}\right)$
をとる。
第3問(選択問題)(配点20)
数列$\{a_n\}$は,初項$a_1$が$0$であり,$n=1,2,3,\cdots$のとき次の漸化式を満
たすものとする。
$a_{n+1}=\frac{n+3}{n+1}\{3a_n+3^{n+1}-(n+1)(n+2)\}\cdots\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$
(1)$a_2=6\ \ \left(\fbox{ア}\right)$である。
(2)$b_n=\frac{a_n}{3^n(n+1)(n+2)}$とおき,数列$\{b_n\}$の一般項を求めよう。
$\{b_n\}$の初項$b_1$は$0\ \ \left(\fbox{イ}\right)$である。$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$の両辺を$3^{n+1}(n+2)(n+3)$で割
ると
$
\frac{a_{n+1}}{3^{n+1}(n+2)(n+3)}=\frac{1}{3^{n+1}(n+2)(n+3)}\frac{n+3}{n+1}\{3a_n+3^{n+1}-(n+1)(n+2)\}\\
=\frac{1}{3^{n+1}(n+1)(n+2)}\{3a_n+3^{n+1}-(n+1)(n+2)\}\\
=\frac{a_n}{3^{n}(n+1)(n+2)}+\frac{1}{(n+1)(n+2)}-\frac{1}{3^{n+1}}\\
$
となるので
$b_{n+1}=b_n+\frac{1}{(n+1)(n+2)}-\left(\frac{1}{3}\right)^{n+1} \ \ \left(\fbox{ウ},\fbox{エ},\fbox{オ},\fbox{カ}\right)$
を得る。ただし、$\fbox{エ}<\fbox{オ}$とする。
したがって
$b_{n+1}-b_n=\left(\frac{1}{n+1}-\frac{1}{n+2}\right)-\left(\frac{1}{3}\right)^{n+1} \ \ \left(\fbox{キ},\fbox{エ},\fbox{オ},\fbox{カ}\right)$
である。
ここで
$
\begin{array}{cccc}
& b_{2}-b_1&=&\left(\frac{1}{2}-\frac{1}{3}\right)-\left(\frac{1}{3}\right)^{2} \\
& b_{3}-b_2&=&\left(\frac{1}{3}-\frac{1}{4}\right)-\left(\frac{1}{3}\right)^{3} \\
&&\cdot& \\
&&\cdot& \\
&&\cdot& \\
+)& b_{n}-b_{n-1}&=&\left(\frac{1}{n}-\frac{1}{n+1}\right)-\left(\frac{1}{3}\right)^{n} \\ \hline
&b_n-b_1&=&\frac{1}{2}-\frac{1}{n+1}-\left(\left(\frac{1}{3}\right)^{2}+\left(\frac{1}{3}\right)^{3}+\cdots +\left(\frac{1}{3}\right)^{n}\right)
\end{array}
$
つまり
$n$を$2$以上の自然数とするとき
$\displaystyle{\sum_{k=1}^{n-1} \left(\frac{1}{k+1}-\frac{1}{k+2}\right)=\frac{1}{2}-\frac{1}{n+1}=\frac{1}{2}\left(\frac{n-1}{n+1}\right)}\ \ \left(\fbox{ク},\fbox{ケ},\fbox{コ}\right)$
また$\displaystyle{c_n=\sum_{k=1}^{n-1} \left(\frac{1}{3}\right)^{k+1}}$とおくと
$
\begin{array}{cccc}
&c_n&=&\left(\frac{1}{3}\right)^{2}+\left(\frac{1}{3}\right)^{3}+\cdots +\left(\frac{1}{3}\right)^{n}\\
-)&\frac{1}{3}c_n&=&\left(\frac{1}{3}\right)^{3}+\left(\frac{1}{3}\right)^{4}+\cdots +\left(\frac{1}{3}\right)^{n+1}\\ \hline
&\frac{2}{3}c_n&=&\left(\frac{1}{3}\right)^{2}-\left(\frac{1}{3}\right)^{n+1}
\end{array}
$
より
$
c_n=\frac{3}{2}\left(\left(\frac{1}{3}\right)^{2}-\left(\frac{1}{3}\right)^{n+1}\right)=\frac{1}{6}-\frac{1}{2}\left(\frac{1}{3}\right)^{n}
\ \ \left(\fbox{サ},\fbox{シ},\fbox{ス},\fbox{セ}\right)
$
が成り立つことを利用すると
$
b_n=\frac{1}{2}\left(\frac{n-1}{n+1}\right)-\frac{1}{6}+\frac{1}{2}\left(\frac{1}{3}\right)^{n}\\
=\frac{3n-3}{6(n+1)}-\frac{n+1}{6(n+1)}+\frac{1}{2}\left(\frac{1}{3}\right)^{n}\\
=\frac{n-2}{3(n+1)}+\frac{1}{2}\left(\frac{1}{3}\right)^{n}\ \ \left(\fbox{ソ},\fbox{タ},\fbox{チ}\right)
$
が得られる。これは$n=1$のときも成り立つ。
(3) (2)により、$\{a_n\}$の一般項は
$
a_n=b_n 3^{n}(n+1)(n+2)
=\left(\frac{n-2}{3(n+1)}+\frac{1}{2}\left(\frac{1}{3}\right)^{n}\right) 3^{n}(n+1)(n+2)\\
=3^{n-1}(n^2-4)+\frac{(n+1)(n+2)}{2}\ \ \left(\fbox{ツ},\fbox{テ},\fbox{ト},\fbox{ナ},\fbox{ニ},\fbox{ヌ}\right)
$
で与えられる。ただし、$\fbox{ナ}<\fbox{ニ}$とする。
このことから、すべての自然数$n$について、$a_n$は整数となることがわかる。
(4) $k$を自然数とする。$a_{3k},a_{3k+1},a_{3k+2}$を$3$で割った余りは
$\ell$を自然数とする。
$
a_{3k}=3^{3k-1}\{(3k)^2-4\}+\displaystyle{\frac{(3k+1)(3k+2)}{2}}\\
=3\times 3^{3k-2}\{(3k)^2-4\}+\displaystyle{\frac{9k(k+1)+2}{2}}\\
=3\times 3^{3k-2}\{(3k)^2-4\}+9\ell+1\equiv 1 (\mod 3)\\
a_{3k+1}=3^{3k}\{(3k+1)^2-4\}+\displaystyle{\frac{(3k+2)(3k+3)}{2}}\\
=3\times 3^{3k-1}\{(3k+1)^2-4\}+\displaystyle{\frac{9k(k+1)+6k+6}{2}}\\
=3\times 3^{3k-2}\{(3k)^2-4\}+9\ell+3k+3\equiv 0 (\mod 3)\\
a_{3k+2}=3^{3k+2}\{(3k+2)^2-4\}+\displaystyle{\frac{(3k+3)(3k+4)}{2}}\\
=3\times 3^{3k+1}\{(3k+2)^2-4\}+\displaystyle{\frac{9k(k+1)+12k+12}{2}}\\
=3\times 3^{3k+1}\{(3k+2)^2-4\}+9\ell+6k+6\equiv 0 (\mod 3)\\
$
だから、それぞれ$1,0,0$である。$\ \ \left(\fbox{ネ},\fbox{ノ},\fbox{ハ}\right)$
また、$\{a_n\}$の初項から第$2020$項までの和を$3$で割った余りは
初項から第$2020$項までの各項で$\equiv 1 (mod 3)$となるものは
$2020=673 \times 3+1$より$673$個で他は$\equiv 0 (\mod 3)$、したがって
$673=224 \times 3+1 \equiv 1$だから
$\displaystyle{\sum_{k=1}^{2020} a_{k} \equiv 1 (\mod 3)}\ \ \left(\fbox{ヒ}\right)$である。
第4問(選択問題)(配点 20)
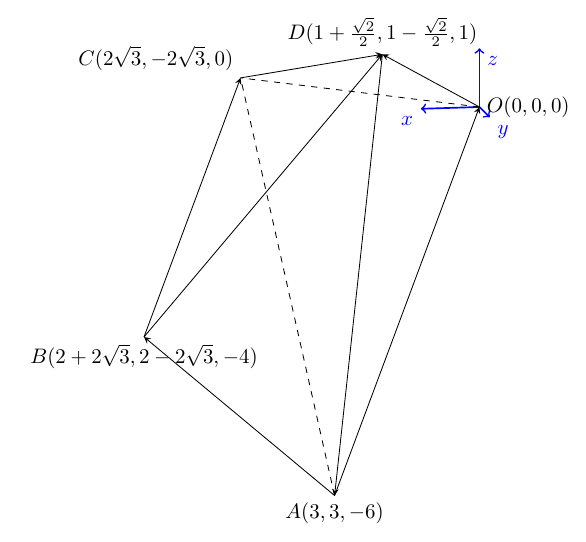
点$O$を原点とする座標空間に$2$点
$A(3,3,-6),B(2+2\sqrt{3},2-2\sqrt{3},-4)$
をとる。$3$点$O,A,B$の定める平面を$\alpha$とする。また,$\alpha$に含まれる点$C$は
$\overrightarrow{OA}\perp \overrightarrow{OC},\overrightarrow{OB}\cdot \overrightarrow{OC}=24 \ \cdots \ \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$
を満たすとする。
(1) $\ |\overrightarrow{OA}|=\sqrt{3^2+3^2+(-6)^2}=\sqrt{9+9+36}=3\sqrt{6}\ \ \left(\fbox{ア},\fbox{イ}\right),\\
|\overrightarrow{OB}|=\sqrt{(2+2\sqrt{3})^2+(2-2\sqrt{3})^2+(-4)^2}=\\
\sqrt{4+8\sqrt{3}+12+4-8\sqrt{3}+12+16}=4\sqrt{3}\ \ \left(\fbox{ウ},\fbox{エ}\right)$
であり、
$ \overrightarrow{OA}\cdot \overrightarrow{OB}=(3,3,-6)(2+2\sqrt{3},2-2\sqrt{3},-4)\\
6+6\sqrt{3}+6-6\sqrt{3}+24=36\ \ \left(\fbox{オ},\fbox{カ}\right)
$
である。
(2)点$C$は平面$\alpha$上にあるので,実数$s,t$を用いて,$\overrightarrow{OC}=s\overrightarrow{OA}+t\overrightarrow{OB}$と表
すことができる。このとき,$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$から
$
s\overrightarrow{OC}=\overrightarrow{OA}+t\overrightarrow{OB}=(3s+(2+2\sqrt{3})t,3s+(2-2\sqrt{3})t,-6s-4t)\\ \\
\overrightarrow{OA}\cdot \overrightarrow{OC}\\
(3,3,-6)\cdot (3s+(2+2\sqrt{3})t,3s+(2-2\sqrt{3})t,-6s-4t)\\
=9s+(6+6\sqrt{3})t+9s+(6-6\sqrt{3})t+36s+24t=0\\
54s+36t=0\\
3s+2t=0\\ \\
\overrightarrow{OB}\cdot \overrightarrow{OC}\\
=(2+2\sqrt{3},2-2\sqrt{3},-4)\cdot (3s+(2+2\sqrt{3})t,3s+(2-2\sqrt{3})t,-6s-4t)\\
=(2+2\sqrt{3})\times \{3s+(2+2\sqrt{3})t\}+(2-2\sqrt{3})\times \{3s+(2-2\sqrt{3})t\}+(-4)\times (-6s-4t)=24\\
(6+6\sqrt{3})s+(4+8\sqrt{3}+12)t+(6-6\sqrt{3})s+(4-8\sqrt{3}+12)t+24s+16t
=24\\
36s+48t=24\\
3s+4t=2
$
だから
$s=-\frac{2}{3},t=1$である。$\ \ \left(\fbox{キ},\fbox{ク},\fbox{ケ}\right)$
したがって、
$
\overrightarrow{OC}=(-2+2+2\sqrt{3},-2+2-2\sqrt{3},4-4)=(2\sqrt{3},-2\sqrt{3},0)\ $
より
$
|\overrightarrow{OC}|=\sqrt{(2\sqrt{3})^2+(-\sqrt{3})^2+0^2}=2\sqrt{6}\ \ \left(\fbox{サ},\fbox{シ}\right)
$
である。
(3)$\overrightarrow{CB}=(2+2\sqrt{3}-\sqrt{3},2-2\sqrt{3}+2\sqrt{3},-4-0)=(2,2,-4)\ \ \left(\fbox{ス},\fbox{セ},\fbox{ソ},\fbox{タ}\right)$である。
したがって,平面$\alpha$上の
四角形$OABC$は$\fbox{チ}$。$\fbox{チ}$に当てはまるものを,次の$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 0\kern .06em}}$〜$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 4\kern .06em}}$のうちか
らーつ選べ。ただし,少なくとも一組の対辺が平行な四角形を台形という。
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 0\kern .06em}}$正方形である
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 1\kern .06em}}$正方形ではないが,長方形である
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 2\kern .06em}}$長方形ではないが,平行四辺形である
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 3\kern .06em}}$平行四辺形ではないが,台形である
$\require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 4\kern .06em}}$台形ではない
$
\overrightarrow{OC}\cdot \overrightarrow{CB}
=(2\sqrt{3},-2\sqrt{3},0)\cdot (2,2,-4)=4\sqrt{3}-4\sqrt{3}-0=0
$より、
$\angle OCB=90^{\circ}$。また、仮定より、$\angle AOC=90^{\circ}$だから
$\overrightarrow{OA},\overrightarrow{CB}$は平行。
$[答]
\ \require{cancel}{\scriptstyle\enclose{circle}{\kern .06em 3\kern .06em}}\ \ \left(\fbox{チ}\right)$
$\overrightarrow{OA}\perp \overrightarrow{OC}$であるので,四角形$OABC$の面積は
$
\frac{1}{2}|\overrightarrow{OC}|\times (|\overrightarrow{OA}|+|\overrightarrow{CB}|=\frac{1}{2}\times 2\sqrt{6}\times (3\sqrt{6}+2\sqrt{6})=30\ \ \left(\fbox{ツ},\fbox{テ}\right)$
である。
(4)$\overrightarrow{OA}\perp \overrightarrow{OD},\overrightarrow{OC}\cdot \overrightarrow{OD}=2\sqrt{6}$かつ$z$座標が$1$であるような点$D$の座標は
$
\overrightarrow{OD}=(u,v,1)
$
とおくと
$
\overrightarrow{OA}\cdot \overrightarrow{OD}
=(3,3,-6)\cdot (u,v,1)=3u+3v-6=0 \\
u+v=2\\ \\
\overrightarrow{OC}\cdot \overrightarrow{OD}=(2\sqrt{3},-2\sqrt{3},0)\cdot (u,v,1)=2\sqrt{3}u-2\sqrt{3}v+0=2\sqrt{6}\\
u-v=\sqrt{2}\\
$
より$\ u=1+\frac{\sqrt{2}}{2},v=1-\frac{\sqrt{2}}{2}$
だから
$
D\left(1+\frac{\sqrt{2}}{2},1-\frac{\sqrt{2}}{2},1\right)
\ \ \left(\fbox{ト},\fbox{ナ},\fbox{ニ},\fbox{ヌ},\fbox{ネ},\fbox{ノ}\right)
$
である。このとき
$
|\overrightarrow{OD}|=\sqrt{(1+\frac{\sqrt{2}}{2})^2+(1-\frac{\sqrt{2}}{2})^2+1^2}=\sqrt{2\times \frac{6}{4}+1}=2\\
\cos \angle COD=\frac{\overrightarrow{OC}\cdot \overrightarrow{OD}}{|\overrightarrow{OC}||\overrightarrow{OD}|}=\frac{2\sqrt{6}}{2\sqrt{6}\times 2}=\frac{1}{2}
$
より
$\angle COD=60^{\circ}\ \ \left(\fbox{ハ},\fbox{ヒ}\right)$である。
$3$点$O,C,D$の定める平面を$\beta$とする。$\alpha$と$\beta$は垂直であるので,三角形
$ABC$を低面とする四面体$DABC$の高さは
$|\overrightarrow{OD}|\sin \angle COD=2\frac{\sqrt{3}}{2}=\sqrt{3}\ \ \left(\fbox{フ}\right)$
である。
したがって,
四面体$DABC$の体積は
$
V_{D-OABC}-V_{D-AOC}\\
=\frac{1}{3}S_{OABC}\times \sqrt{3}-\frac{1}{3}\times \triangle AOC \times \sqrt{3}\\
=\frac{1}{3}\times 30\times \sqrt{3}-\frac{1}{3}\times \frac{1}{2} \times |\overrightarrow{OC}|\times |\overrightarrow{OA}| \sqrt{3}\\
=\frac{1}{3}\times 30\times \sqrt{3}-\frac{1}{3}\times \frac{1}{2} \times 2\sqrt{6} \times 3\sqrt{6} \times \sqrt{3}=10\sqrt{3}-6\sqrt{3}\\
=4\sqrt{3}
\ \ \left(\fbox{ヘ},\fbox{ホ}\right)
$
である。
戻る
|