円周角の問題等
円周角の問題等
$$(1)次の図で点Oは円の中心である。\angle x の大きさを求めなさい。$$ (以下、拙い図もありますがご容赦)
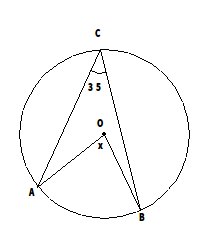
$$x=2\times 35=70^\circ$$
$$(2)$$
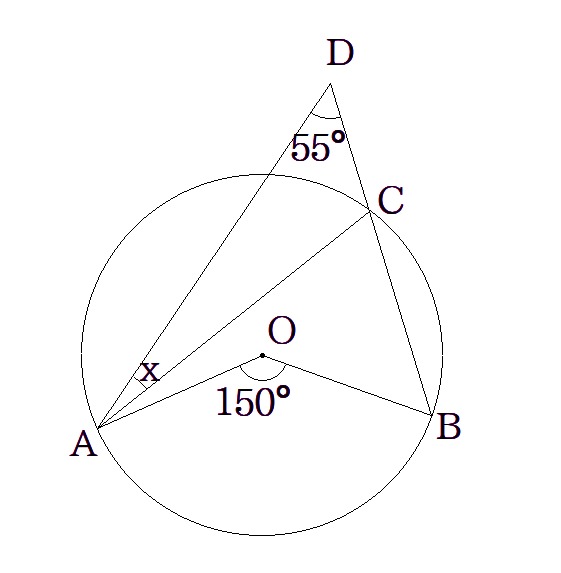
$$\angle DAC +\angle ADC=x+55=\angle ACB=\frac{1}{2}\angle AOB=\frac{1}{2}\times 150=75$$ $$x+55=75$$ $$x=20^\circ$$
$$(3)次の図でx の値を求めなさい。$$
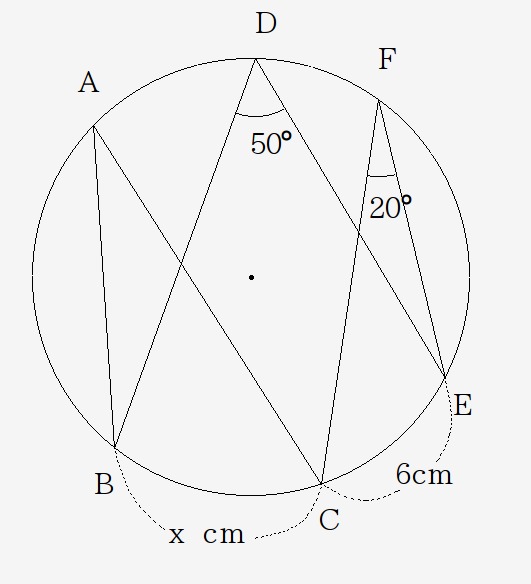
$$20:50=6:(6+x)$$ $$20(6+x)=300$$ $$6+x=15$$ $$x=9(cm)$$ または、$$\angle BAC=\angle BDE-\angle CFE=50-20=30より$$ $$20:30=6:x$$ $$20x=180$$ $$x=9(cm)$$
$$(4)次の図で\stackrel{ \Large \frown }{AE}=\stackrel{ \Large \frown }{ED}\ AB,CDは直径のとき、\angle xの大きさを求めなさい。$$
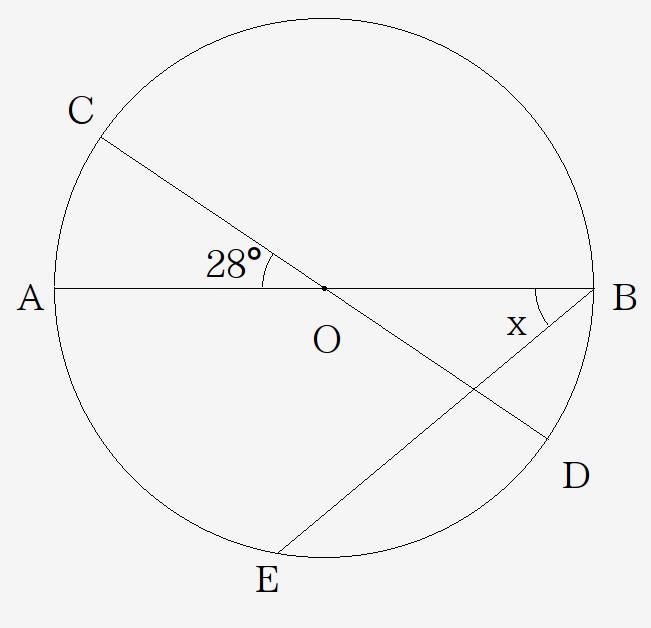
$$\angle AOD=180^\circ-28^\circ=152^\circ$$ $$\stackrel{ \Large \frown }{AE}=\stackrel{ \Large \frown }{ED}より$$ $$\angle AOE=\frac{1}{2}\angle AOD=\frac{1}{2}\times 152=76^\circ$$ $$\angle x=\frac{1}{2}\angle AOE=\frac{1}{2}\times 76=38^\circ$$
$$(5)次の図で点Oは円の中心である。\angle x の大きさを求めなさい。$$
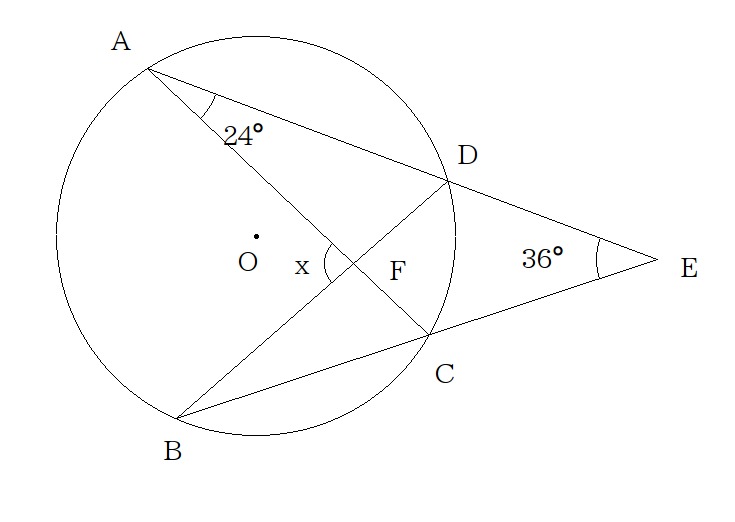
$$\angle ACB=24^\circ+36^\circ=60^\circ(\triangle ACE の外角)$$ $$x=\angle CFD(対頂角,\triangle CBF の外角)$$ $$=\angle ACB+\angle CBD$$ $$\angle CBD=\angle CAD(\stackrel{ \Large \frown }{CD}の円周角)だから$$ $$=\angle ACB+\angle CAD=60^\circ+24^\circ=84^\circ$$
$$(6)$$
$$BC=a,CA=b,AB=c\ の\triangle ABCで、内接円が辺BC,CA,AB$$
$$に接する点をそれぞれD,E,Fとするとき、AEの長さを求めなさい。$$
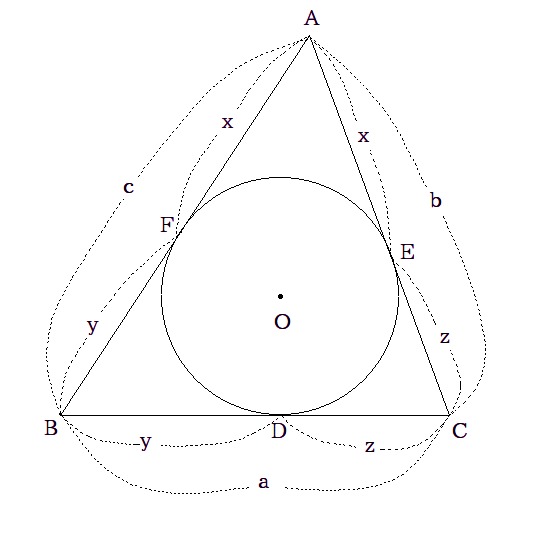
$$解答$$ $$図のように、\triangle ABC の内心を Oとします。$$ $$F,D,Eは内接円と3辺の接点とする。$$ $$\triangle AEOと\triangle AFOにおいて$$ $$\ \ AOは共通$$ $$\ \ \angle AEO=\angle AFO=90^\circ\ \ (接線と半径)$$ $$\ \ EO=FO\ \ (円Oの半径)$$ よって、直角三角形の斜辺と他の一辺がそれぞれ等しいので $$\ \ \triangle AEO \equiv \triangle AFO$$ $$よって、AE=AFがいえる。同様に、BD=BF,CD=CE$$ $$y+z=a\cdots(1)$$ $$x+z=b\cdots(2)$$ $$x+y=c\cdots(3)$$ $$(1)+(2)+(3)\ \ \ 2(x+y+z)=a+b+c$$ $$\hspace{1cm}x+y+z=\dfrac{a+b+c}{2}$$ $$右辺は\triangle ABCの周の長さの半分であるから、これをとくにsとおく。$$ $$すなわち、 s=\dfrac{a+b+c}{2}とすると$$ $$x+y+z=s\cdots(4)$$ $$(4)-(1)より\ \ x=s-aとなり、$$ $$AE=x=\dfrac{b+c-a}{2}となる。$$