$$V=\frac{1}{n}\times I^{1/2}\times R^{2/3}$$ $$この計算では、水深を管形と等しくすれば、円管（満流時）の値となる。$$ $$円管（満流時）のみの計算にする場合は、下の式より\theta=2\piだから、$$ $$R=\frac{A}{S}=\frac{D}{4}\left(1 -\frac{\sin \theta}{\theta}\right)=\frac{D}{4}\left(1 -\frac{\sin 2\pi}{2\pi}\right)=\frac{D}{4}$$ $$として必要な修正を施せばよい。$$ $$＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊$$ 図（２）より、
$$水深をh,円管の半径をrとおくと、\theta は次のように計算できる。$$ $$r\left(1-\cos \frac{\theta}{2}\right)=h$$ $$1-\cos \frac{\theta}{2}=\frac{h}{r}$$ $$1-\cos \frac{\theta}{2}=\frac{h}{r}$$ $$\cos \frac{\theta}{2}=1-\frac{h}{r}$$ $$\frac{\theta}{2}=\cos^{-1}\left(1-\frac{h}{r}\right)$$ $$\theta=2\cos^{-1}\left(1-\frac{h}{r}\right)$$ $$ここでr=\frac{D}{2}を代入して$$ $$\theta=2\cos^{-1}\left(1-\frac{h}{\frac{D}{2}}\right)=2\cos^{-1}\left(1-\frac{2h}{D}\right)$$ これと、以下で得た式をjavascriptで実現したのが、最上部の計算である。
$$＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊＊$$ $$Q=AV\ \ (1)$$ $$A=\frac{D^2}{8}(\theta -\sin \theta)\ \ (2)$$ $$S=\frac{D}{2}\theta\ \ (3)$$ $$R=\frac{A}{S}=\frac{\frac{D^2}{8}(\theta -\sin \theta)}{\frac{D}{2}\theta}=\frac{D^2}{8}(\theta -\sin \theta)\times \frac{2}{D\theta}=\frac{D}{4}\left(1 -\frac{\sin \theta}{\theta}\right)\ \ (4)$$ 流水の断面積
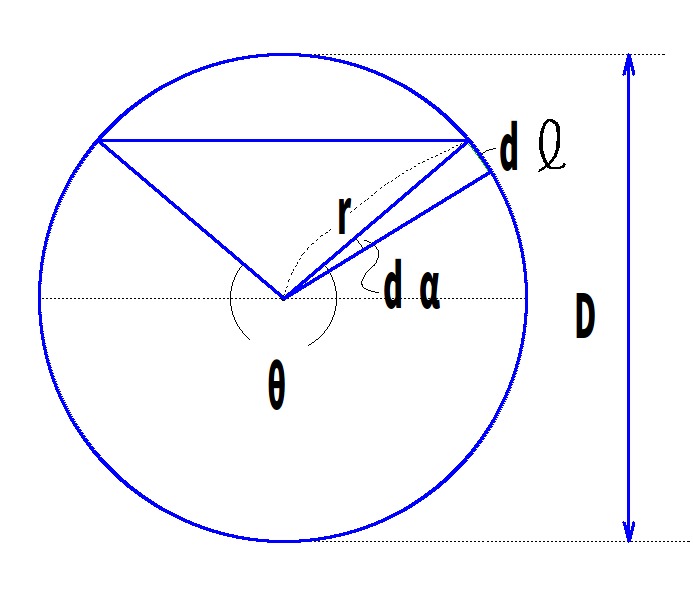図（１）
　　　$$A:図（１）の図の扇形部分の面積に、その上の三角形の面積を加えればよいので$$ 　　　$$まず、扇形の面積を求めると\frac{\pi D^2}{4}\times \frac{\theta}{2\pi}\ \ \ （2-1)$$ 　　　$$次に、三角形の面積を求めると\frac{1}{2}\times \frac{D^2}{4}\sin (2\pi-\theta)=-\frac{1}{2}\times \frac{D^2}{4}\sin \theta\ \ \ （2-2）$$ 　　　 　　　　$$（2-1）と（2-2）を加えて整理すると\frac{\pi D^2}{4}\times \frac{\theta}{2\pi}-\frac{1}{2}\times \frac{D^2}{4}\sin \theta=\frac{D^2}{8}(\theta -\sin \theta)\ \ \ （2）になる。$$ 　　$$S:中心角\thetaの扇形の円弧を求めると\pi D\times \frac{\theta}{2\pi}=\frac{D}{2}\thetaで、(3)になる。$$ 　　　　　　　　(http://www.asahi-net.or.jp/~YM7K-INUE/を参考にした) $$*********************************$$ $$ネット上には流水断面積(A)を求めるのに、一般に知られた扇形や三$$ $$角形の面積公式などを使わず、積分を使って求めている例もある。こ$$ $$こでは「水と数学」をテーマとしたので、敢えてそれを書くことにした。$$ 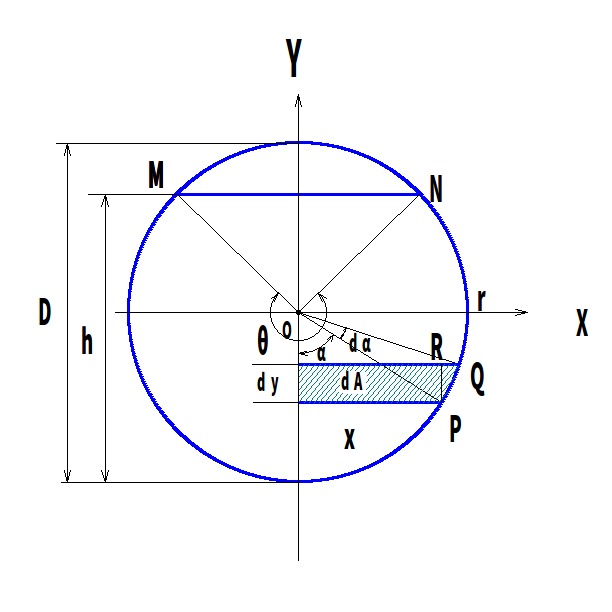図（２）
$$図（２）のように、Ｙ軸との任意の中心角\alphaに対して、微小な角度d\alpha$$ $$をとり、円周との交点をP,Qとすると、\overline{PQ}\cong \stackrel{ \Large \frown }{PQ}=rd\alpha$$ $$また、d\alphaは微小だからOP\perp PQとしてよい。したがって、\angle PQR=\alpha\ だから、$$ $$dy=\overline{PR}=\overline{PQ}sin \ \alpha=rd\alpha \sin \alpha$$ $$また、x=r\sin\ \alpha$$ $$点P,Qからy軸に下ろした垂線の足をそれぞれ、$$ $$S,T（図にないが）とおき、領域PQRSの面積をdAとすると、$$ $$dA=xdy=r\sin \alpha\times rd\alpha \sin \alpha=r^2sin^2 \alpha \ d\alpha$$ よって、
$$A=2\int_{\alpha=0}^{\frac{\theta}{2}}dA$$ $$\ =2r^2\int_{0}^{\frac{\theta}{2}}\sin^2 \alpha\ d\alpha=r^2\int_{0}^{\frac{\theta}{2}}(1-\cos 2\alpha)d\alpha $$ $$\ =r^2\left[\alpha-\frac{\sin 2\alpha}{2}\right]_{0}^{\frac{\theta}{2}}=r^2\left(\frac{\theta}{2}-\frac{\sin \theta}{2}-0+\frac{\sin 0}{2}\right)=\frac{r^2}{2}(\theta-\sin \theta)$$ $$r=\frac{D}{2}を代入して$$ $$A=\frac{D^2}{8}(\theta -\sin \theta)\ \ (2)$$ $$のようになるが、どちらもよい求め方だと感心した。$$ 　（http://coala.chips.jp/civil/workroom.htmを参考にした）
ここに、
Ｑ：流量
Ｖ：平均流速
ｎ：粗度係数（水路壁面、底面の粗さを示す値で、水路の材質や状態により異なる。）
R：径深（水理学的平均水深とも言う。　流積を潤辺で割ったもの）
S：潤辺（水路断面において、水が周囲の壁や底と接する長さ。）左上の図の---の長さ。
Ａ：水路における流水の断面積
　 θ：水面と中心とのなす角（ｒａｄｉａｎ単位）　度の場合はｒａｄ単位に変換する必要がある。
Ｉ：動水勾配　ｈ_ｆ/Ｌ　（ｈ_ｆ：エネルギー損失　　　Ｌ：水路延長）
但し、等流では、動水勾配＝水面勾配＝水路床勾配であるので、計算には水路床勾配を用いることが多い。