正多面体や準正多面体
まあ、紙工作と呼んでも良いのだが、多少は計算も必要だったりするので
表題だけは紙工学(Paper Engineering)と格好をつけておくことにしましょう。
今は遠くの大学で流体力学の研究を本業とする
友人がその名付け主であり、数少ない同朋です。
正多面体や準正多面体
このあたりは、ただ寸法通りに切って貼ればできるので難しくないでしょう。
準正多面体というのは、正多面体の制約を「複数の種類の正多角形
を使っても可」としたもので、例えばサッカーボールなんかもその一つです。
交差した円柱の共通部分、または和集合
例えば、3本の等しい半径の円柱がそれぞれ垂直に交差している物体の共通部分は
紙で作成可能です。
それぞれの紙片は、y=r*sin(x/r)と位相をpi/2ずつずらした曲線で囲まれた
領域になります。
(下図は円柱2本の場合。木の葉のような領域4枚で構成される)
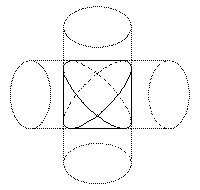
この発展形として、4本の円柱がそれぞれcos(x)=-1/3となる角度で交差した物体の 共通部分や和集合を考えてみましょう。和集合はテトラポッドみたいな形になります。
ペンローズの三角形
下のような構造物を紙で作ろうという試みがあります。もちろんまともに作ることは できないので、正面から見たときにそのように見えるような物体を作ろうというものです。
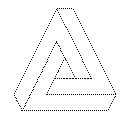
友人のページを参照ください。
紙で作成可能なものとは
定義は結構面倒です。例えば、球はだめですが円錐はOKです。
特異点でない面上の任意の点に対して
半径drの微少な球で切り取られる面の切り口の長さが2*pi*drと一致すること
で必要十分なのかどうかは深く検討していません(全然違うと思われる)。
研究中のもの
1枚の紙を過不足なく用いて作成できる物体があるかどうかを考えています。
例えば立方体は、頂点に集まるのは90度*3=270度ですので、90度分の紙が余りますね。この余分な紙は、切り取るか折り込むかしなくてはならないわけです。
そのような操作(切り取る、折り込む)を必要としない物体は存在するでしょうか？
中が空洞の円柱や角柱は一応条件を満たしますが、面白い物体ではありません。
正八面体を縦に無限に積んだ柱も、条件は満たします(各頂点には6枚の正三角形が接している)。
あとネタとしては、螺旋のスロープを考えています。tan(z)=x/yで 表される曲面を紙で作成できるでしょうか？
created by H.M 00.04.03