πの桁数の伸び
πの計算は古くは少なくとも紀元前17世紀から行われていた。日本ではまだ縄文時代も始まっていません。
初めの頃は西洋とインドで主に計算が行われていました。
逆三角関数を用いた無限級数の式が発見された17世紀後半からは、自分が発見した公式を用いて計算する人も多いです。
●西洋・インドでの計算
| 年代 |
人物・地域・出典 |
方法・公式 |
記録・πの値 |
| B.C.1650頃 |
アーメス・パピルス(エジプト) |
直径9の円と一辺8の正方形の面積が大体等しい |
256/81=約3.16 |
| B.C.1600頃 |
スーサ書板(バビロニア) |
正六角形の円周(別に内接や外接する物ではない) |
3.125 |
| B.C.500頃 |
シュルバスートラ(インド) |
|
3.09 |
| B.C. 250頃 |
アルキメデス(ギリシャ) |
円に内接・外接する正96角形の面積 |
211875/67441=約3.1416 |
| B.C.150頃 |
ウマスヴァティー(インド) |
正6角形・正12角形を内接 |
3.16 |
| 87-165 |
プトレマイオス |
|
195882/62351=約3.16016 |
| 260頃 |
劉徽(中国) |
正96角形の辺の長さ |
3.1416 |
| 480 |
祖沖之(中国) |
正24576角形の辺の長さ |
3.1415926 |
| 500 |
アールヤバタ(インド) |
内接正384角形の辺の長さ? |
3.1416 |
| 937-1038 |
アルクワリズミ(アラビア) |
|
3.141745・・・ |
| 1114-1185 |
バースカラ |
|
3.1416,3.141666・・・ |
| 1400 |
マーダヴァ(インド) |
無限級数展開 |
小数点以下11桁 |
| 1429 |
アル=カーシー(ペルシャ) |
正805306368(3*2^28)角形の辺の長さ |
小数点以下16桁 |
| 1527-1607 |
アドリアン・メティウス |
|
355/113=約3.1415929 |
| 1540-1603 |
ピエタ |
正393216(3*2^17)角形の面積 |
小数点以下10桁 |
| 1579 |
フランソワ・ヴィエート |
正393216(3*2^17)角形の辺の長さ |
小数点以下9桁 |
| 1593 |
アドリアン・パン・ルーマン(オランダ) |
|
小数点以下9桁 |
| 1561-1615 |
ロマヌス |
正83886080(2^24*5)角形の面積 |
小数点以下15桁 |
| 1596 |
ルドルフ(Ludolf van Ceulen) |
正515396075520(2^35*3*5角形の面積 |
小数点以下20桁 |
| 1540-1610 |
ルドルフ(Ludolf van Ceulen) |
正4611686018427387904(2^62)角形の面積 |
小数点以下35桁 |
| 1665 |
アイザック・ニュートン |
|
小数点以下15桁 |
| 1706 |
アブラハム・シャープ |
|
小数点以下71桁 |
| 1706 |
ジョン・マチン |
マチンの公式 |
小数点以下99桁 |
| 1719 |
ド・ラグニー |
|
小数点以下126桁 |
| 1794 |
ベガ |
|
小数点以下139桁 |
| 1824 |
ウィリアム・ラザフォード |
|
小数点以下151桁 |
| 1844 |
ヨハン・ダーゼ |
ダーゼの公式 |
小数点以下204桁 |
| 1847 |
トーマス・クラウゼン |
|
小数点以下247桁 |
| 1853 |
ウィリアム・ラザフォード |
|
小数点以下439桁 |
| 1855 |
リヒター |
|
小数点以下499桁 |
| 1874 |
ウィリアム・シャンクス |
マチンの公式 |
小数点以下526桁 |
| 1946 |
ファーガソン |
|
小数点以下619桁 |
| 1947.1 |
ファーガソン |
|
小数点以下709桁 |
| 1947.9 |
ファーガソン |
|
小数点以下807桁 |
●日本での計算
日本人も昔から計算していました。古く木こりの間では大体3ということになっていました。江戸時代にはいろいろな方法で計算されていたようです。一時は世界に並ぶほど進んでいました。
1627年の塵劫記によれば、第四十七 開平円法の事に次のようにかかれている。
この一尺三寸四方あるものを丸くなしてはさしわたしなにほどになるぞというときに、
さしわたし一尺四寸六分二厘五毛になるなり。
法に、右に一一二五と置きてこれに一尺三寸を掛くれば、さしわたし一尺四寸六分二厘五毛となるなり。
また、一寸四方の坪、七百十一坪ある時、開平円法にさしわたしなにほどになるぞというときに、
さしわたし三尺になるなり。
法に七百十一坪を右に置きて円法七十九をもって割れば九百坪になる。それを開平法にて割れば三尺になるなり。
注:10寸=1尺 10分=1寸 10厘=1分 10毛=1厘
1坪は1尺四方の正方形の面積
簡単に訳すると、
1尺3寸四方の正方形を円にすると直径がいくらになるかといえば、1尺4寸6分3厘5毛になる。
なぜなら1.125(9/8)に1尺3寸を掛ければ1尺4寸6分3厘5毛になるからだ。
また、1寸四方の坪で711坪の円があるときその直径がいくらになるかといえば3尺になる。
なぜなら711を円法の0.79で割れば900坪になる。これの平方根を取って3尺(30寸)になる。
ということです。紀元前16世紀ぐらいの考えを日本ではまだ用いていたようです。
後の塵劫記によれば、円法79とあります。これは直径の二乗に掛けて面積を計算する物であるから、これから円周率を求めると3.16となります。
七九の説明については第二十 開平円法の事に次のように書かれている。
七九といふ事は、円さしわたし一尺あれば、一寸の坪七九坪有。一尺を二つに割れば五寸有。又一分を二つに割れば五厘と成。これに五寸を掛くれば二十五と成。これに三尺一寸六分を掛くれば七十九坪に成ゆへに、七九を掛ける也。
この文章は少し意味の分からないところがあるが、とにかく円周率を3.16と思っていたことは事実のようである。当時は半径で面積を計算をしたのではなく半径中心に考えていたからそのようになったようである。
この本が書かれたのは寛永20年であるから西暦1643年である。そのころはあまり円周率を求めることが行われていなかったらしい。
その後は無限級数による計算も行われていたらしい。
| 年代 |
人物 |
方法・公式 |
記録 |
| 1661 |
村松茂清 |
正32768角形の面積 |
3.141592648776 |
| 1674 |
古郡之政 |
|
22/7,157/50,355/113 |
| 1683 |
奥田有益 |
|
3.14 |
| 1683 |
磯村吉徳 |
|
3.1416 |
| 1696 |
古郡解 |
|
3.14166136832 |
| 1712 |
関孝和 |
|
3.14159265359微弱 |
●コンピューターによる計算
πのコンピューターによる計算は1949年にアメリカのENIACで2037桁が正しく計算されたことから始まります。当時は2037桁計算するのに70時間もかかったそうです。
| 発表年 | マシン | 国 | 公式 | 記録 |
| 1949 | ENIAC | アメリカ | マチン | 2,037 |
| 1955 | NORC | アメリカ | | 3,089 |
| 1957 | PEGASUS | イギリス | | 7,480 |
| 1958 | IBM-704 | フランス | | 10,000 |
| 1959 | IBM-704 | フランス | | 16,167 |
| 1959 | IBM-7090 | イギリス | | 20,000 |
| 1961 | IBM-7090 | アメリカ | | 100,265 |
| 1966 | CDC-6600 | フランス | | 250,000 |
| 1967 | IBM-7030 | フランス | | 500,000 |
| 1986 | CRAY-2 | アメリカ | | 29,360,000 |
| 1987 | SX-2 | 日本 | | 133,550,000 |
| 1988 | HITAC S-820/80 | 日本 | | 201,326,000 |
| 1995 | HITAC S-3800/480 | 日本 | ボールウェインの4次 | 3,221,120,000 |
| 1995 | HITAC S-3800/480 | 日本 | ボールウェインの4次 | 4,294,960,000 |
| 1995 | HITAC S-3800/480 | 日本 | | 6,442,450,000 |
| 1997/7/24 | HITACHI SR2201 | 日本 | ボールウェインの4次 | 51,539,600,000 |
| 1999/5/13 | | 日本 | ガウス・ルジャンドル | 68,719,470,000 |
| 1999/9/20 | HITACHI SR8000 | 日本 | ガウス・ルジャンドル | 206,158,430,000 |
| 2002/11/24 | HITACHI SR8000/MPP | 日本 | 逆正接関数(高野喜久雄氏の発見)の公式 | 1,241,100,000,000 |
<<前回の記録についての詳細>>
2つの計算方法で計算した206,158,430,208桁(=3*2^36桁)の内、206,158,430,163桁まであっていた(最後の45桁が異なっていた)ので、安全性と記憶のしやすさを考慮して、206,158,430,000桁(約2060億桁)を記録とした。小数点以下2000億桁目は2である。桁数が前の世界記録より約3倍にものびているにもかかわらず、計算時間は2時間ほどしかのびていない。これは1秒間に全体で1兆回も計算する128台の計算機を並列で計算した結果であるとも言える。
主計算にかかった時間は37時間21分04秒、主記憶容量は865GB。
計算は1999年9月20日の午前8時21分56秒に終了した。(日本標準時)
東京大学情報基盤センタースーパーコンピューティング研究部門の金田教授らが成し遂げた。
<<今回の記録についての詳細>>
小数点以下1兆桁目は2最後は045であった。これは1秒間に全体で2兆回も計算する並列型のスーパーコンピューターで計算した結果である。しかし、その機能が最大限に使われたものではないらしい。詳細は金田教授がホームページにて発表するとされているが、なかなかされていない。
主計算・検証計算などあわせて約600時間。
驚くべきは桁数もさることながらその計算方法である。今まで行われていたものとは全く異なり、ENIACやそれ以前に手計算で行われていたものと同じArctangentを用いた計算方法なのである。全く想像ではあるが、今まではFFT(高速フーリエ変換)を用いて10進数で計算していたものと考えられる(Super πでもその計算方法らしい。もちろん内部演算は2進数。)のに対し、DRM法(分割有理数化法)を用いて16進数で計算したとのこと。それで、得られた16進数での結果を10進数に表記し直した。
前回と同じく東京大学情報基盤センタースーパーコンピューティング研究部門の金田教授らが成し遂げた。
|
πの桁数の伸びのグラフです。別に最高値だけを結んだ訳ではないので所々下がっているところもあります。
手計算で行っていた最初の方はずっと多角形の周りの長さや多角形の面積によって求められていました。
1600年後半からは無限級数による計算が盛んに行われるようになり、桁数が伸びていきました。
その後コンピューターの登場までは、新しい公式の発見が桁数の伸びに大きな影響を与えていたようです。
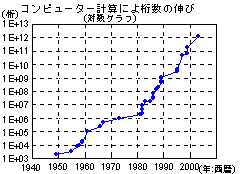
一気に桁数が伸びたのはコンピューターの登場した1949年以降です。
その後桁数の伸びに変化があるのは、コンピューターの進化や新しい公式の発見、さらにはアルゴリズム(計算方法)の改良があったからです。
現在は、大体5000億桁が限界ではないかといわれています。でも、この調子で行けば2010年までには1兆桁まで求まりそうです。
|
予想よりはるかに早く1兆桁を越えました。金田教授らは「今後はなかなか記録が伸びないのでは・・」と発表したらしいが、今後もまた記録が伸ばされるのかもしれない。
|
今後はインターネットを利用して全世界のコンピューターを使った計算も行われるかもしれません。
グラフの縦軸の1E+3とは1000、1E+4とは10000のことです。 | 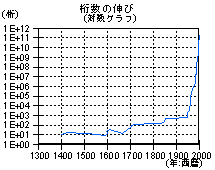
|

