第一章　輸送網における輸送問題の定式化

1.1 相補性定理

　この定理を理解するのに一番良い方法は生産計画を分析してみることである。　一般の生産計画は次のように定式化されることはよく知られている。

a11x1 + a12x2 + ……… + a1n xn ≦ b1
a21x1 + a22x2 + ……… + a2n xn ≦ b2
……………………
am1x1 + am2x2 + ……… + amn xn ≦ bm
xn ≧ 0 n = 1,2,3,……,n という条件のもとで
c1x1 + c2x2 + ……… + cn xn → 最大化
これに対する双対問題は双対変数をy1,y2,…ym とすると次のように定式化される。
a11y1 + a21y2 + ……… + am1ym ≧ c1
a12y1 + a22y2 + ……… + am2ym ≧ c2
……………………
a1ny1 + a2ny2 + ……… + amnym ≧ cn
yn ≧ 0 m = 1,2,3,……,m という条件のもとで
b1y1 + b2y2 + ……… bmym → 最小化
さてこれらの問題の最適解をそれぞれx*,y* とするとき次の関数が成立する。
主問題のi行の制約式について
(A) ai1x1* + ai2 x2* + ……… + ainxn* ＜ bi
となるi(i番目の原料)に対してyi* （原料iの限界価値）= 0となる。
即ち　yi*(bi - ainxn*) = 0
主問題のj列に関する双対問題の制約式について
(B) a1jy1* + a2jy2 * + ……… + amjym* ＞ cj
となるj(j番目の製品)に対してxj* （製品jの生産量）= 0 となる。
即ち　xj*(amjym* - cj) = 0
証明：
①　b - ax = u
②　y'a - c = v'
とおく ①式の両辺にy'を掛けると
③　y'u = y'b - y'ax
同様に②式の両辺にxを掛けると
④　v'x= y'ax - c'x
③式と④式のそれぞれを足すと　y'u + v'x = y'b - c'x となる。
ところで線形計画法デュアル定理により、x,y が最適解であるための必要十分条件は y'b = c'x であるから、y'u + v'x = 0 にならなければいけない。
ところで u,v,x,y ≧ 0 であるから
　　y'u= 0　　　v'x = 0 になる


数式だけの説明では分かりにくいかと思われるので、経済的な意味でこれらの関係を表現すると、(A)は最適計画が実行されたとき結果的に余剰の出るような資源の価額（限界価値）は０であることを意味する。(B)については左辺は製品ｊを一単位生産するのに要する資源の総価値、別な言葉で表現すると、限界価値によって評価された各原料も総価値が、その商品からもたされる収入 Cj よりもお大きいならば、その商品は生産されないということである。以上の説明で相補性の定理が表現する数字の経済的な意味を多少は理解されたと思う。

1.2　ヒッチコック型輸送問題の定式化

図１

簡単なヒッチコック型輸送問題は、例えば倉庫Ｗから都市Ｃに輸送する図１ のようなモデルを考えてみればすぐに定式化できる。
即ち、ある倉庫(W1)から出荷される物質の和は、在庫量（Ｓ）を超えては ならないという在庫量からくる制約条件式が一組ある。
x11 + x12 + x13 ≦ S1
x21 + x22 + x23 ≦ S2
x31 + x32 + x33 ≦ S3
また、各都市に流入する物質の和は、その都市が必要としている需要量 （Ｄ）を超えなければならない、という需要量から導かれる制約条件式がもう 一組ある。
x11 + x12 + x13 ≧ D1
x21 + x22 + x23 ≧ D2
x31 + x32 + x33 ≧ D3
xij ≧0　　i=1,2,3　　j=1,2,3
目的関数として、各ルートの輸送費用を Cijとすれば
Z = ∑ij Cijxij → 最小化
という形になり、最も基本的なＬＰの問題として多くの会社で利用されている。

1.3　ネットワークにおける輸送問題の定式化とその双対問題

　さてネットワークにおける輸送問題は、前節のヒッチコック型のように供給量と需要量からくる制約式では不充分で、中継点に対しても何らかの制約を設けなければならない。そこでネットワークの場合には次のようなモデルを考え定式化してみる。

図２

  1. ∑i∈A(0) X0i = D
  2. ∑i∈B(j) Xij - ∑k∈A(j)xjk = 0
  3. ∑∈B(n) Xin = D
  4. 0 ≦ Lij ≦ Xij ≦ Kij
  5. Z = ∑ij CijXij → 最小化
ここで
B(j) = { 点 j に向う有向枝があるような点 i の集合 }
A(j) = { 点 j から出る有向枝があるような点 k の集合 } であり。
i ∈ B(j), k ∈ A(j) は i と k が、それぞれ B(j), A(j)に含まれる点であることを示している。
    各式を説明すると
  1. １式は点０において流れｄが起ったことを示している。
  2. ２式は流量保存法則（途中の点で、流れが目減りしないから（点ｊに入ってくる流れの量）－（点ｊから出ていく流れの量）＝０とすれば明らかである。
  3. ３式は点ｎにおいて流れが消滅することを意味している。
  4. ４式は輸送路 i → j に設けられる制約条件で、道路網に例えば上限の Kj は、そのルートに送り得る最大限の量を示し、下限のLij は何らかの理由でそれぞれ以上輸送しなければならないという条件をつけられたときなどに設定される。
  5. ５式は輸送路 i → j の一単位あたりの輸送コストをCij とし、それに流量を掛けて費用を求め、全ての枝について総合したものである。

　巡回(Circulation)

　さて前項の式をみたとき、１式と３式は点０で流れｄが発生し、点ｎで流れｄが消滅したことを意味するが、これはある意味で冗長な式である。何故ならば図２に見られるように点ｎから点０に還流するルート（点線）を付け加えることにより、すべて２式の流量保存法則の式に帰属できる。従って以後は流れではなく、巡回(Circulation)という言葉を使って説明する。即ち問題を次のような簡単な形に定式化し、最適巡回を求めることに置き換える。

  1. ∑i∈B(j) Xij - ∑k∈A(j)xjk = 0 J = 0,1,… n
  2. Lij ≦ Xij ≦ Kij
  3. Z = ∑ij CijXij → 最小化
　この定式化した問題は次のような双対問題になる。
  1. -Ui + Uj + (U'ij - U"ij) ≦ Cij
  2. Ui, Uj 自由変数　U'ij, U"ij ≧ 0
  3. ∑ij (LijU'ij - KijU"ij) →最大化
 　ここにUi,Uj はそれぞれ点i,jに設定される相対変数でポテンシャルとよばれる任意の実数である。 U'ij,U"ij は枝 i → j のそれぞれ下限、上限に対する双対変数で非負の値をとる。

1.4　相補性定理の適用

　さて今まで述べてきた問題で、最適巡回が得られたとするならば、各枝に関して相補性の定理を適用すると次の３式が成立する筈である。

  1. U'ij ( Xij - lij ) = 0
  2. U"ij,( Kij - Xij ) = 0
  3. Xij { Cij + Ui - Uj - (U'ij - U"ij) } = 0
　これらの式のうち、1.および 2.は主問題の各枝についての下限及び上限からくる制約条件式　と、それぞれの双対変数から導かれる。3.式は双対問題の制約条件式とその双対変数（双対問題の双対変数であるから、即ち主問題の主変数でXij となる）から導かれるものである。
　これらについて表現を変えてもう少し詳しく説明してみると、最適巡回における各枝の状態は必ず次の３つの状態のどれかに相当する筈である。

　① Xij = Lij　かつ　U"ij = 0　かつ　 U"ij = Cij + Ui - Uj ≧ 0
　② Lij ＜ Xij ＜ Kij　かつ　 U'ij = U"ij = Cij + Ui - Uj = 0
　③ Xij = Kij　かつ　U'ij = 0　かつ　 U"ij = -(Cij + Ui - Uj) ≧ 0
①の枝については、流量は下限に等しく、従って上限の制約条件式は満たされないからその双対変数は０となり、更に3.式より、下限の双対変数（非負である）
U"ij = Cij + Ui - Uj ≧ 0 となる訳である。
②の枝は流量が上限と下限の間にあって、上限および下限の相対変数は共に０となり、
Cij + Ui - Uj = 0となる。
同様に③の枝は、流量が上限に等しく、そのため下限の制約条件は満たされないから０となり、上限の相対変数は
U"ij = -(Cij + Ui - Uj) ≧ 0 となる。これらの枝の状態でCij + Ui - Uj の値が何らかの重要な役目を果たしていることに気がついておられると思う。

1.5　輸送問題と相補性定理の適用の経済的解釈

　ここから少し経済的な解釈に重点を置きながら話を進めてみたい。

図3

図4


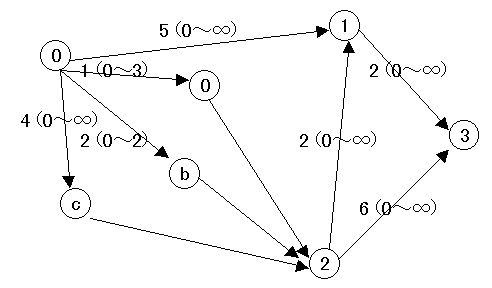
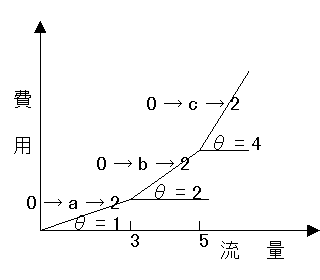
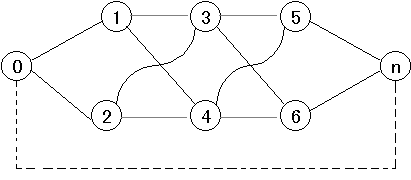
図３のようなごく簡単なネットワークを考えてみる。図３において、各枝につけられた数字はその枝に１単位のものを輸送したときの費用で、（ ）内はその費用で流し得る流量である。
特に枝０→２については道幅が狭く混雑しやすいので、図４に見られるように流量が多いと急激に費用が高くなっていく枝であるとする。この場合ネットワークにおいては枝０→２の間に仮の点ａ，ｂ，ｃを設け、費用別に３本の枝が同時に存在しているように取り扱う。
　さてここで、各枝の輸送コストをその枝の距離とみなし、点０（供給点）から各中継点への最短距離をもとめてラベル付けを行う。各点のラベルはそれぞれ（０）、（１）、（３）、（５）となり最短路は０→２→１→３となる。各点のラベルは最短距離の累積であるから、その点が物を購入する際、もっとも安い輸送路を選んで買った場合の輸送コストであるといえる。従ってもし最短路を構成する枝に容量制限が無ければ、流れは専らこれらの枝に集中するであろう。
　ところで、これら各点のラベルにマイナス符号をつけたものが前節に出てきたポテンシャルに相当するのである。それは恰も電流が電位の高い所から低い方へ流れるように、流れがポテンシャルの高い所から低い方に向かって生ずることを意味する。
　さて経済社会では、物流は必ず価額の安い所から高い方に向かって生ずる。そこでラベルの値を、その点の原価（生産原価を除いた）と見立てて話を進めてもそれほど不自然ではないと考える。そこで以後はポテンシャルの反対符号にした値を、その点における原価とみなして話を進めていく。
　次に、再び前節のCij + Ui - Uj という式を思い出していただきたい。この式の意味するところを次に説明する。
図５


　点ｊに流入する枝が２本あるとする。枝ｉ→ｊに関して、点ｉの原価はＵｉ でありｉ→ｊ間の輸送費用はＣｉｊ であるから、枝ｉ→ｊを通ったときの点ｊにおける原価はCij + Ui になる。同様に、枝ｌ→ｊの場合には、点ｊにおける原価はCli + Ul となる。ここで枝ｌ→ｊが点ｊまでの最短路と仮定すると
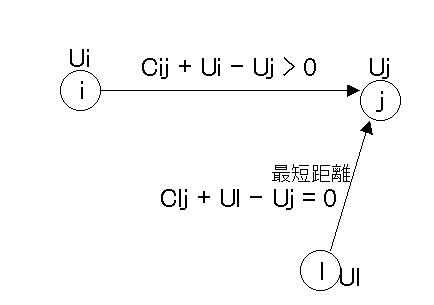
、 　　Clj + Ul = Uj　　→　　 Clj + Ul - Uj = 0
また枝ｉ→ｊについては、最短路ではないから
　　Cij + Ui ＞ Uj　　→　　 Cij + Ui - Uj ＞ 0　となる。
　具体的な例として、図３の点に注目していただきたい。点１がもし点２から１単位購入すれば輸送コストは３｛点２の原価＋（枝２→１の輸送コスト）｝となる。これはこの輸送路が前に述べたように、費用からみた最短路であるから当然である。ところが点１がもし点０から直接購入したとしたらどうであろうか。図３から明らかなように輸送コストは５となり (Clj + Ui - Uj = 5 + 0 - 3 = 2 ＞ 0) 不利であることがすぐ分かる。
　このようにして全ての枝に関して、Cij + Ui ＞ Uj の値が正となるか、０となるか、あるいは負となるかを常に監視していれば、ある枝に流れを起こすことが損か特かを簡単に判断することができる。
そこで
　　　　Cij = Cij + Ui - Uj とおくと
  1. Cij ＞ 0 ：この枝に流すと損である。
  2. Cij ＝ 0 ：この枝は任意に流して良い。
  3. Cij ＜ 0 ：この枝は得だから流すべき。
となる。

　3.式は、このような枝がもし存在するとしたら、その枝が最短路となって Cij=0 となる筈であるが、この訳は図３枝０→ａ→２ の費用１の枝について考えてみれば分かる。この枝は容量が３であるから、それ以上の流れを起こしたいときは費用２の枝 （０→ｂ→２） に流すしかない。しかし現在の点２の原価は１であるから、これを２にすることにより、枝０→ｂ→２ にも流すことができる。すると枝０→ａ→２の Cijは Cij + Ui - Uj　= 1 + 0 - 2= -1 ＜ 0 で負となる。従って流量は当然その枝の上限に張り付き、上限を超えた分がもっとも高い費用の枝に流れることになる。

　さて今までの説明で、輸送すると損と分かっている枝には流れを生じさせなければ良いのであるが、安い枝に流したくとも、容量制約（Kij ）があるため高い枝にも流さなくてはならないとか、或いは世間に義理、人情で高いと分かっていても、ある量だけは決められた所から買わねばならないというような制約（Lij ）をしばしばうけることがある。このようなルートは当然ある量（Lij ）までしか流さず、それ以上は流さないことが賢明である。

輸送網流量最小費用計算メンページへ