第二章 Out-of-Kilte法の計算手順
2.1 アルゴリズム
- 各枝の適合性チェック
繰り返すようであるが、相補性の定理から最適巡回時に各枝がとるべき状態は次の3つのどれかである。
- L : Cij > 0 かつ
Xij = lij
- B : Cij = 0 かつ
lij ≦ Xij ≦ Kij
- K : Cij < 0 かつ
Xij = Kij
即ち状態Lの枝は損であるから、要求された下限の流量しか流さない事とし、Bの枝は最短路を構成しているから、許容範囲内で任意の値を取れる。そしてKの枝は大変得であるから目いっぱい流す事とする。
このようにしてネットワーク内のすべての枝がL、B、K、のどれかの状態を取るとすると、それは最適な巡回と言えるであろう。そこで、これらの枝の状態を最小費用という目的に適っているという意味で適合(In-kilter)な枝と呼ぶ。
次に最適巡回に到達していない時点における任意の巡回においては、何本かの枝は次の6種類の状態のどれかを取っている。これらは不適合(Out-of-kilter)な枝と呼ばれる。
- L1 : Cij > 0 かつ
Xij < lij
- L2 : Cij > 0 かつ
Xij > lij
- B1 : Cij = 0 かつ
Xij < lij
- B2 : Cij = 0 かつ
Xij > Kij
- K1 : Cij < 0 かつ
Xij < Kij
- K2 : Cij < 0 かつ
Xij > Kij
これら不適合な枝は次に述べる方法を施すと適合な状態に追い込むことができる場合が多い。第一の方法は流れを変えることであり、第二の方法は原価(ポテンシャル)を強制的に変化させて、その結果として流れを変えることである。そこで、例えばある枝がL1の状態の場合、その流れを
lijまで増流(lij - Xij
)すれば適合な状態にすることができる。この(lij - Xij
)を不適合な枝の偏差または"Kilter
Numbers"(適合にするには、あと流れを何単位増減すれば良いかという数値)と呼ぶ。従って最終的にすべての枝の偏差を0にすれば、それは最適巡回といえるであろう。
- ラベリング
前項で枝の偏差を0にするため流れを変えることを述べたが、それを実行する手段として強力なのがラベリングである。
図6
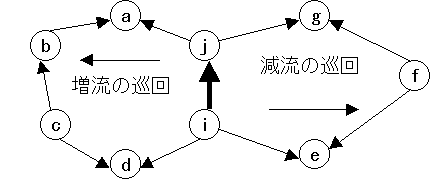
ある枝i→jが不適合だと仮定し、その枝の流量を1単位増加したいとする。そのためには、例えば点jからj→a→b→c→d→i,
というような巡回を考える。そのとき巡回を構成するいかなる枝の偏差をも増加しないよう注意しなければならない。このような巡回を構成できたならば、ラベリングと同じ方法の枝(枝ij、枝ja、枝cd)に対しては流量を1単位増加する。逆方向の枝(枝ba,枝cb、枝di)に対しては流量を1単位減らす。他方、枝i→j
の流量を1単位減らしたときは、点iからラベリングを始めi→e→f→g→j
というような巡回を構成する。勿論、各枝の偏差は増大しないようにすべきである。後は増流巡回と同様その巡回に含まれる各枝の流量をその矢印に従って増減する。このように流量変化のための巡回を見つけることをラベリング手順という。
- ラベリング手順
-
不適合な枝を見つけたら、増流、減流の目的に従い、ラベリングを始める点を0、終点をnとする。
- 始点0にラベル(" ",∞)をつける。ラベルの前の数字は、その点にどの点から
ラベルがついたかを示し、後の数字その点までにどの位の流量を増加させる事ができる
かを示す。
- ある点iに点hからラベル(h、αi)がついたものとする。点iに
枝をもっている点で、まだラベリングされていないすべての点jを考えるとき、それら
の間の枝が次のような状態であれば、その点jに対しラベリングする事ができる。
----------------------------------------------
図7
|
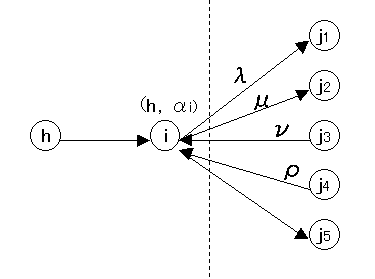
|
(i,Min[αi,lij−xij]) |
(i,Min[αi,kij−xij]) |
(i,Min[αi,xij−lij]) |
|
(i,Min[αi,xij−kij]) |
| ラベリング不能 |
|
ラベリングされている.....→.....ラベリングしようとする点
----------------------------------------------
λ:Cij > 0 かつ Xij < lij
μ:Cij ≦ 0 かつ Xij < kij
ν:Cij ≧ 0 かつ Xij > lij
ρ:Cij < 0 かつ Xij > kij
新しくラベリングされた各点の増加可能流量はそれぞれ
Min[αi,lij−xij]、
Min[αi,kij−xij]、
Min[αi,xij−lij]、
Min[αi,xij−kij]となる。
この手順で終点nがラベリング[l,αn]されたとすると、その巡回
(0→a→b→……→i→j→……→n)において、
順方向の矢印を持つ枝はαn増流し、逆方向の枝はαn減流
することができる。こうして構成された巡回の中では、いかなる枝の流量をαn
増減しても、その枝の偏差が増加しないことは明白であろう。それどころか、いくつか
の不適合な枝はその偏差を減少する。
もし終点nがラベリングできないときは、次に述べる原価(ポテンシャル)
変更の原価を強制的に操作する方法を使って、最終的に流量変更のための巡回を 作り出す工夫をする。
原価(ポテンシャル)の変更
前項で述べたラベリング手順によって常に終点nがラベリングできれば良いが、どうしてもこれ以上ラベリングできないという事態が生じることがある。
例えば点iまでラベリングでき、その後点jにラベリングできなくなったと仮定する。
----------------------------
図8
|
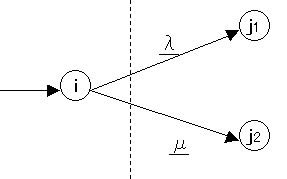
|
この時の状態は次の2種類のどちらかになる。
λ:Cij > 0 かつ Xij > lij
μ:Cij ≦ 0 かつ Xij ≧ kij
|
ラベリングされている→されていない
----------------------------
この状態は、それぞれラベリングできる状態λ、μの反対(流れがとる範囲)
の関係になることから分かっていただけると思う。ところでこのとき、状態μ
はいかなる工夫をしても流量増加が偏差の増大につながる。しかし状態λ
の場合は、Cijを0にすれば流量を増加できる可能性を秘めている。
即ちラベリングされる可能性を持っている。
-------------------------------
図9
|
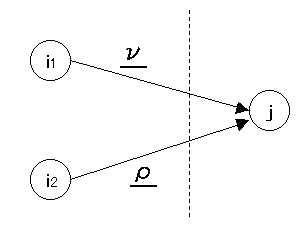
|
同様に図9において、点jがラベリングされて、そこに流入している枝をもつ点iがラベリングできないと仮定すると、枝i→jは次の状態のどれかになる。
ν:Cij ≧ 0 かつ Xij ≦ lij
ρ:Cij < 0 かつ Xij ≦ kij
|
ラベリングされていない→されている
-------------------------------
状態νは、どのようにしても減流できないが、ρの場合は、Cij
を0にすれば、流量が下限制約(lij
)を超えている分だけ減らすことができる。この二つの枝の状態λとρ
はラベリングが進まなくなった時点において、重用な解決策を与えている。
そこで、どうしてもこれ以上ラベリングが進まないという局面において、I
をラベリングされた点の集合、Iをラベリングできない点の集合とする。そして
そこに行き交う枝をもってカットを形成する。このカットに属する枝のうち次の
状態を持つ枝の集合を考える。
S1={(i,j)|i∈I,j∈I,Cij>0,Xij≦kij}
S2={(i,j)|i∈I,j∈I,Cij<0,Xij≧lij}
S1は増流できる可能性を持った枝λの集合を意味し、S2
は減流できる可能性を持った枝ρの集合である。そして原価変更する値θ
を次のように定める。
θ=Min[S1集合:Min(Cij),S2集合:Min(-Cij)]
S1=S2=0のとき θ=∞
もしカットにおいてラベリングを続ける可能性のある枝がない(S1=S2=0)
とすれば、この問題は解を持たない。又、もしθをある値に設定できるならば、
カットに接するラベリングされた各点iの原価を、状態S1、S2
に従って強制的にθ上げ下げする(ポテンシャルをθ変化させる)。
この結果新しいポテンシャルを得る。
- Ui=Ui+θ i∈I
- Ui=Ui i∈I
又、Cijの新しい値は
- Cij=Cij+θ :(i,j)∈(I,I)
- Cij=Cijーθ :(i,j)∈(I,I)
- Cij=Cij :その他の枝
枝の損得を判断するCijが変化し、S1かS2
のうち少なくとも1本の枝(S1のときは状態μに、S2
のときは状態νに)はラベリング可能な枝に変化する。このようにCij
を操作することによりラベリングできる点を増加し、何回かの後、目的とする流量
変化の巡回を完成する訳である。
またθの選択は状態S1の枝については本来Cij> 0
で、流れを増やすと損である。しかし強制的にCijを0[送り
側(売り手)が原価を割引したとする]に変え、損はないとして増流する訳である
から、その変化量(費用増加分)θは最小とすべきである。同様に状態S2
の枝についても、本来Cij<0で得た枝であるから、上限一杯
に流したい枝の筈である。しかしわざとCijを0[受取側(買い手)
が原価が安いと振舞う]に変え、得はないとして減流しようとする訳であるから、
その変化量(値上がり分)θはやはり最小にすべきであることがわかる。
このように不適合なすべての枝についてラベリング手順を施し、流量変化と原価
(ポテンシャル)の変更を適宜繰返しながら一本つづ適合な枝に変え、ついには最適
巡回に到達することができる。
Out-of-Kilter法 フローチャート
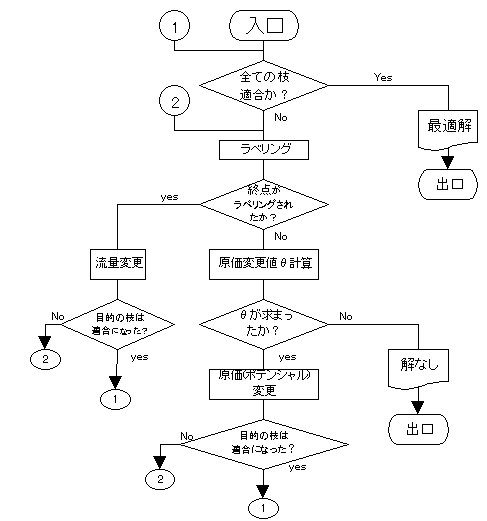
輸送網流量最小費用計算メンページへ




