3.8 Geometric primitives
このカテゴリはシーンの幾何学的な部分を記述するためのシェイプ(幾何学的プリミティブ)あるいはソリッド(セットオペレーションを使用するシェイプの組み合わせ)を作成する、全ての指令を再編成します。
VirtuaLightインターフェイスは22の異なるシェイプを提供します。
どのシェイプも Shpae [ ] 構造体で記述されなければなりません。
シェイプの定義はレンダラがサーフェイスをそのライティングの特徴とその変形と、どのように関連付けるかを定義します。
この定義は最初にプリミティブのシェイプを含まなければなりません、それからオプションで、シェーダ定義、変形の定義、シェイプの修飾定義が続きます。
基本的にはシェイプはこの様に定義されます。
Shape [
Specific shape description
Shader reference (optionally shader modifiers)
Transformation modifiers
Shape modifiers (bound, subdivisions, attributes)
]
このセクションでは全てのシェイプ (セクション3.8.1から3.8.22) と構造的なソリッド幾何学図形 (セクション3.8.23)
を定義を記述します。
セクション 3.9 シェイプの修飾定義の記述
セクション 3.12 変形の修飾定義の記述
セクション 3.13 シェーダ定義の記述
どのようなシェイプ構造体でも宣言されることが可能です。
どのプリミティブも後でシェイプ構造体をincludeするために、別々に宣言する事が可能です。
プリミティブの定義はそれ自身が構造体ではなく、指令です。
それで、この形式で与えられます:
Primitive(argument1, argument2, …, argument n)
それぞれにシェイプの記述は次のようなサブセクションで与えられます。
(アルファベット順)
3.8.1 Bicubic patch
バイキュービックパッチは各エッジがキュービック曲線の3D曲面です。
それはパラメーターとして4つの制御点を使用してカーブの形を決定する方程式である、2次基底関数を使用します。
VirtuaLight インターフェイスの基底関数組込セットは、Bezier、B-Spline、Catmull-Rom、そしてHermiteを含んでいます。
パッチは4x4配列の制御点で定義されます。
シンタックスは:
BicubicPatch (int basis, int ustep, int vstep, [ 16 comma-separated
vertices ] )
最初の引数は基底関数タイプを設定します。アーカイブファイル "statics.vib" にはそれらが静的に宣言されています。
static BEZIER = 1
static BSPLINE = 2
static CATMULLROM = 3
static HERMITE = 4
For each basis, the actual basis matrix is:
Bezier
[ -1,3,-3,1, 3,-6,3,0, -3,3,0,0, 1,0,0,0 ]
B-Spline
[ -1,3,-3,1, 3,-6,3,0, -3,0,3,0, 1,4,1,0 ]
Catmull-Rom
[ -1,3,-3,1, 2,-5,4,-1, -1,0,1,0, 0,2,0,0 ]
Hermite
[ 2,-2,1,1, -3,3,-2,-1, 0,0,1,0, 1,0,0,0 ]
2番目と3番目の引数はそれぞれの方向の、パッチの細分化のレベル数を設定します。
より多くの細分化が指定された場合、パッチの近似はよりスムーズになりますが、レンダリングにはより長い時間が掛かります。
その後の角カッコの間には、パッチを記述する16ポイントのリストが続きます。
パッチのコーナーは、ポイント1、ポイント4、ポイント13そしてポイント16です。
バイキュービックパッチ定義の例:
Shape [ BicubicPatch(BEZIER, 6, 6,
(1.4, 2.4, 0), (1.4, 2.4, -0.78), (0.78, 2.4, -1.4), (0, 2.4,
-1.4),
(1.33, 2.53, 0), (1.33, 2.53, -0.74), (0.74, 2.53, -1.33), (0,
2.53, -1.33),
(1.4375, 2.53, 0), (1.43, 2.53, -0.8), (0.8, 2.53, -1.43), (0,
2.53, -1.43),
(1.5, 2.4, 0), (1.5, 2.4, -0.84), (0.84, 2.4, -1.5), (0, 2.4,
-1.5) ) ]
3.8.2 Blobby
Blobbyは自由形式 (free-form) 自己混合 (self-blending) 陰関数 (implicit-function)
サーフェイスとして定義する事が可能です。
それは周囲のものあるいは球形、円柱あるいは平面コンポーネントの、スムーズにするポテンシャルフィールドを記述します。
それぞれのコンポーネントは力の眼に見えないフィールドです、そしてそれは特定の強さでスタートし、与えられた半径か所定の距離において、0にスムーズに低下します。
どこでこれらのコンポーネントが空間でオーバラップしても、これらのフィールドの強さは共に加算されます。
ひとつとその他のコンポーネントの相互作用からシェイプを作成して得るために、blobbyの定義は少なくともふたつのコンポーネントを持たなければなりません。
blobbyは球体 (sphere)、円柱 (cylinder) あるいは平面 (plane) をコンポーネントとして使用可能なので、シンタックスはとても奇妙です。
Blobby (float threshold, list of components separated by a comma)
threshold 引数は全体の強度の値です、そしてそれはblobbyを眼に見えるようにします。
blobby中のどのようなポイントも、この閾値の強度にマッチところでシェイプのサーフェスを形成します。
blobbyが持つ事ができるコンポーネント/引数の数の制限はありません。
しかしより多くのコンポーネントはレンダリングが完了するまでにより長くかかるでしょう。
それぞれの異なるコンポーネントのためのシンタックスはプリミティブのものと同じです、しかし最後に強度のパラメータが追加されます。
この強度の記述は、コンポーネントの中心の周囲のポテンシャルフィールドがどれくらいの強度か、そしてコンポーネントが他のコンポーネントに相互作用する最大の距離の半径値の記述です。
正の強度の値はblobbyコンポーネントを引き付けてお互いに流れるように動く原因になります。
負の強度の値は他のコンポーネントを撥ね付けるかあるいはへこみを作る、眼に見えないコンポーネントを作成します。
Sphere(point center, float radius, float strength)
center: 球形コンポーネントの中心-center of the spherical component
radius: 半径-its radius
strength: 強度-its strength
Cylinder(point bottom, point top, float radius, float strength)
bottom : 円柱の最初の終端の軸-the first end of the axis of the cylindrical
component
top : もう一方の終端の軸-the other end of the axis
radius: 半径-its radius
strength: 強度-its strength
Plane(vector normal, float dist, float radius, float strength)
normal : 平面コンポーネントを記述している平面方程式の法線-normal to the plane equation describing
the planar component
dist : 法線に沿った原点からの距離-its distance from the origin along the normal
radius: 相互作用最大距離-its maximum distance of interaction
strength: 強度-its strength
blobby方程式を解くために、VirtuaLight インターフェイスは3つのアルゴリズムを提供します。
それらは FerrariSolver、VietaSolver 、そして SturmSolver です。
デフォルトでは Vieta が使用されます。
ひとつが選ばれると、シェイプ構造体がincludeされなければなりません。
これらの方法についてより知りたい場合はセクション3.9.5を参照してください。
Example of a single blobby definition:
Shape [ Blobby(0.625,
Sphere((0.75, 0, 0), 1, 1),
Sphere((-0.375, 0.64952, 0), 1, 1),
Sphere((-0.375, -0.64952, 0), 1, 1),
Cylinder((0, 0, 1), (0, 0, -1), 0.2, 1),
Cylinder((0, 0, -1), (-0.375, 0.64952, 0), 0.125, 1),
Cylinder((0, 0, -1), (-0.375, -0.64952, 0), 0.125, 1),
Cylinder((0, 0, -1), (0.75, 0, 0), 0.125, 1) )
]
3.8.3 Box
x,yそしてz軸に並べたエッジを持つ、ふたつの対角線の方向の反対側のコーナーで定義された長方形のボリュームを記述します。
反対側の面は平行でそして隣接した面はお互いに直角です。
シェイプが定義された時、おのおのの側面は座標軸に平行です。
boxのアラインメントを変化させるためには、回転はシェイプが定義された後に適用されなければなりません。(しかしまだ同じShape構造体で)
シンタックスは:
Box (point corner1, point corner2)
もし、コーナー1がboxの前下左角を定義するなら、コーナー2は後上右角でなければなりません。
box定義の例
Shape [ Box((-1, -2, 0), (2, 4, 1.5)) Rotate(0, 0, -30) ]
3.8.4 Cone
基部、頂点部に覆いのない円錐形、そして半径、それらのポイントを記述します。
シンタックスは:
Cone (point base, float baserad, point apex, float apexrad)
baseは基部の中心で、baserad はこの基部の半径です。
apex は頂点中心で、apexrad はこの頂点部の半径です。
Cone定義の例:
Shape [ Cone((0,-1,0), 2, (2, 2, 0), 0.75) ]
3.8.5 Cylinder
下部と上部の覆いのない円柱、そして半径を記述します。
シンタックスは:
Cylinder (point bottom, point top, float radius)
bottomはその底側の中心を表すポイントで、topはその上側の中心を表します、そしてradiusはその半径です。
Cylinder定義の例:
Shape [ Cylinder((0,0,0), (-1, 1, 10), 1.5) ]
3.8.6 Disk
円盤の中心、法線そして半径を記述します。
このプリミティブは通常ConeあるいはCylinderのような部分的な2次曲面のtopかbottomを覆うために使用されます。
シンタックスは:
Disk (point center, vector normal, float radius)
Center が円盤の中心を定義し、normal がその方位 (それの垂直方向) を定義し、そしてradius がその半径を定義します。
disk定義の例:
Shape [ Disk((0,1.5,0), (0,1,-1), 1.5) ]
3.8.7 Extruded Surface
与えられた方向に沿って掃引された多角形について記述します。それは多重側面を有するビームを作るかあるいはリボン状のオブジェクトを作成するために使用することができます。
The syntax is:
ExtrudedSurface (int method, int numpoints, vector dir, { list of vertices
between brackets separated by a comma } )
最初の引数は掃引のためのカーブのタイプを指定します。アーカイブファイル "statics.vib" にはそれらが静的に宣言されています。
STRAIGHT = 1
POLYNOMIAL = 2
CONDITIONAL = 3
STRAIGHTは、サーフェイスが単に線分を押し出すだろうということを意味します。それは最も速い方法ですが、それは、鋭い角を備えた直線の端を生成します。
POLYNOMIALは、与えられた線分に接近するスプラインによってサーフェイスが表わされるだろうということを意味します。結果は、形が直線の端か鋭い角のない滑らかな外観を持っているということです。しかしながら、STRAIGHTよりレンダリングに長くかかります。この方法によりroot
solverで使用する、4つのオーダー多項式、3つの指令FerrariSolver、VietaSolverおよびSturmSolverのうちの1つを使用することを指定するためにShape構造に含むことが可能です。
デフォルトでは、Vieta方法が使用されます。これらに関してもっと知るためにセクション3.9.5を参照してください。
CONDITIONALは、頂点がカーブ上になければならないかあるいはカーブ上になくても良いかで、それが可能なところでカーブを使用することを可能にします(0はオンカーブ、1はオフカーブ)。
2番目の引数は定義される頂点の正確な数をセットします。少なくとも2つの点がカーブのために定義されなければなりません、しかしたった2つの点は単純なコーン(円錐形)を構築します。
3番目の引数は押出されたサーフェイスのオリエンテーションを変更するために使用されるベクトル方向です。
例えば(0, 1, 0)はy軸を真っ直ぐに上下するサーフェイスのために指定されます。ベクトル方向のサイズは押出しの量に影響するでしょう(e.g.
方向の絶対値が=2ならば、押出しはその方向へ2ユニットになるでしょう)。
その後、頂点のリストは続きます。点は下記の形式の中で定義されます。
{x,y}
CONDITIONAL方式で、ポイントオフカーブは以下の形式で定義されます:
{0 : x,y} or {OFF : x,y}
また、ポイントオンカーブは以下の形式で定義されます:
{1 : x,y} or {ON : x,y} or simply {x,y}
多角形と異なり、レンダラは自動的にExtrudedSurfaceを閉じません。閉じたsweepを得るための、頂点のリスト中の始点および終点は同じであるに違いありません。CSGオペレーション(セクション3.8.24)の中でそれを使用するために押し出されたサーフェイスを閉じることは重要です。
単一の押し出されたサーフェイス定義の例:
Shape [
ExtrudedSurface(STRAIGHT, 9, (0,0,2),
{1,0},
{1.1, 1},
{2, 1.5},
{2, 2},
{2.5, 2.5},
{1.1, 2},
{1, 4},
{0.5, 4.5},
{0, 4.7} )
SturmSolver
]
3.8.8 Implicit planar height field
ハイトフィールドプリミティブの一般的な定義についてはセクション3.8.13を参照してください。
陰関数ハイトフィールドには2種類あり、平面 (planar) と球形 (spherical) (セクション3.8.8) です。
陰関数平面ハイトフィールドの原理は、特定数の非常に小さい三角形で構成された指定されたグリッドエリアでの数学関数 y = f (x,z)
を評価する事です。
全ての三角形のおのおのの頂点の位置は、その時この関数に基いて計算されます。
シンタックスは:
ImplicitPlanarHeightField (float xmin, float xmax, float zmin, float
zmax,expression, int xsteps, int zsteps)
or
ImplicitPlanarHeightField (float xmin, float xmax, float zmin, float
zmax,expression, int xsteps, int zsteps, SmoothNormal)
2番目のケースでは、SmoothNormal フラグがレンダラにフィールドの全てのポイントで平面のハイトフィールドの法線を計算させます。
それはハイトフィールドにスムーズに見えるサーフェイスをもたらします。
最初の4つの引数は、xとzの最小値と最大値を定義します、そしてそれもまた平面ハイトフィールドのグローバルなサイズを決定します。
Expression は問題の数学的関数を記述します。もちろんこの式もどのような組み込み関数、交点のポイントである実行時変数 Po
あるいは他の有用なポイントの交点浮動小数点を返す関数、でも可能です。
引数 xsteps と zsteps はエリアのそれぞれの方向の解像度を定義します。
より大きな値はスムーズで詳細なハイトフィールドを生み出しますが、しかしより多くのメモリと長い時間のレンダリングを必要とします。
Example of a single implicit planar height field definition:
Shape [
ImplicitPlanarHeightField(-4, 4, -4, 4, 0.3 * cos(x * z + radians(CurrentFrame)),128,
128, SmoothNormal)
]
3.8.9 Implicit spherical height field
ハイトフィールドプリミティブの一般的な定義についてはセクション3.8.13を参照してください。
陰関数ハイトフィールドには2種類あり、平面 (planar) と球形 (spherical) (セクション3.8.8) です。
基本的に球形ハイトフィールドは、サーフェイスの球のベース半径からのオフセットの高さから、ポイントを内部と外部に動かす事により、働きます。
変数関数 u と v は球のエリアを、おのおのの頂点の位置を決定しこの球の全ての小さな三角形を作成するために、評価します。
シンタックスは:
ImplicitSphericalHeightField (float radius, float scale, expression,
int usteps,int vsteps)
or
ImplicitSphericalHeightField (float radius, float scale, expression,
int usteps,int vsteps, SmoothNormal)
2番目のケースでは、SmoothNormal フラグがレンダラにフィールドの全てのポイントで球のハイトフィールドの法線を計算させます。
それはハイトフィールドにスムーズに見えるサーフェイスをもたらします。
最初の引数は球のベース半径を決定します。
2番目の引数は各引数のディスプレイスメント係数を設定します。
値が1.0より大きいは変形を増大させます、一方1.0より小さい値はそれを減少させます。
Expression は問題の数学的関数を記述します。もちろんこの式もどのような組み込み関数、交点のポイントである実行時変数 Po
あるいは他の有用なポイントの交点浮動小数点を返す関数、でも可能です。
最後の2つの引数 usteps と vsteps は球形エリアのそれぞれの方向の解像度を定義します。
より大きな値はスムーズで詳細なハイトフィールドを生み出しますが、しかしより多くのメモリと長い時間のレンダリングを必要とします。
球ハイトフィールド定義の例
Shape [
ImplicitSphericalHeightField(2.75, 1.0, (0.15 * cos(10 * phi)
* cos(10 * theta)),
60, 60, SmoothNormal)
]
3.8.10 Implicit surface
ワールド座標の限定されたエリアの中で 関数 f (x,y,z) の評価により、どのような陰関数サーフェイスも作成を可能にします。(Bound指令による指定)
シンタックスは:
ImplicitSurface (expression)
expression は変数 x,y,z を作成します。
それはオペレータや、VirtuaLight インターフェイスの内部関数そしてどのような種類の数値を含むことが可能です。
陰関数サーフェイスのために、シェイプ修飾指令 Bound (セクション3.9.1) は常に、光線のインターセクションリージョンの限界を定めるShpae構造体で使用されなければなりません。
最終的には他のシェイプの修飾指令 ShapeSubdivision (セクション3.9.4) はサーフェイスがどの程度詳細でなければならないかを設定するのに有用です。
陰関数サーフェイス定義の例:
Shape [
ImplicitSurface(-exp(-x*x-y*y-z*z)+(exp(-x*x*4-z*z*4)+exp(-y*y*4-z*z*4)+exp(-x*x*4-y*y*4))*0.5+0.175)
Bound((-1,-1,-1), (1,1,1))
]
3.8.11 Non-Uniform Rational B-Spline (NURBS)
NURBS カーブはセグメントに分割されたコントロールポイントで指定されるパラメトリックなカーブです。
それぞれのセグメントは数コントロールポイントによって定義されます。
BicubicPatch プリミティブと共に、基底マトリクスは基底関数タイプを決定します。
NURBS プリミティブと共に、カーブの基底関数はノットベクトルと呼ばれる減少しない一続きの数により決定します。
これれらの関数は各コントロールポイントがカーブの位置を指定することにおいて、どのくらいの重要性を持っているかを決定します。
増加する一続きの整数であるノットベクトルは、開いた一様分布 (uniform) ノットベクトルとして知られています。
NURBSカーブはこの種類のノットベクトル、標準B-スプライン基底カーブを使用しています。
増加する一連の整数であるノットベクトルと全てを一緒に混合した浮動小数点は非一様分布 (non-uniform) ノットベクトルとして知られています、そしてそれはBezier、B-スプラインのような特質の、あるいは様々の他のスタイルの、全ての同じカーブの持つコントロールポイントを分割する事を可能にします
VirtuaLight インターフェイスで提供されるNURBSカーブは u と v のパラメータ指示で (更に異なった) どのような命令も可能で、そしてどのような一様分布あるいは非一様分布ノットベクトルも使用することが可能です。
それ以上のNURBSカーブについての詳細は、文献を参照してください。
シンタックスは:
NURBS (int nu, int uorder, uknot[ ], int nv, int vorder, vknot[
], cpoints[ ])
u方向のコントロールポイントの数は nu に等しく、v 方向のコントロールポイントの数は nv に等しくなります。
それでトータルの頂点の数は nu * nv と等しくなります。
order (uorderがu方向、voderがv方向) は基底多項式 (polynomial basis ) の次数プラス1と等しい正の整数でなければなりません。(もしuorderが4と等しければそれはcibicパッチでしょう)
おのおののパラメータの指示にはたくさんの異なるorderがあります、しかしコントロールポイントの数は少なくとも基底多項式のorderと同じくらいに大きくなければなりません。
ノットベクトル (uknot配列とvknot配列) はそれぞれのコントロールポイントと関連付けられます。
それぞれの配列内の値は前の値より小さくてはいけません。(それはイコールであり得ます)
ノット数はコントロールポイントの数+スプラインのorderとイコールです。
cpoints パラメータは頂点の配列の配列を表します。
各頂点は3あるは4の要素を持っているかもしれません。
もし4番目の要素が設定されているなら、スプラインは有理スプラインでしょう。
もし頂点が3つの要素しか持っていないなら、同次 (4番目) の要素はひとつであると考えられます。
同次の要素は0より大きくなければなりません。
シェイプの修飾指令 ShapeSubdivision (セクション3.9.4) はカーブがどれだけ詳細であるかを設定するのに有用である事を注意する必要があります。
NURBSカーブ定義の例
Shape [
NURBS(6, 4, [0, 0, 0, 0, 1.5, 1.5, 3, 3, 3, 3],
5, 4, [0, 0, 0, 0, 1, 2, 2, 2, 2],
[ [ (0,0,0), (1,0,3), (2,0,-3), (3,0,3), (4,0,0) ],
[ (0,1,0), (1,1,0), (2,1,0), (3,1,0), (4,1,0) ],
[ (0,2,0), (1,2,0), (2,2,5,2), (3,2,0), (4,2,0) ],
[ (0,3,0), (1,3,0), (2,3,5,0.5), (3,3,0), (4,3,0)],
[ (0,4,0), (1,4,0), (2,4,0), (3,4,0), (4,4,0) ],
[ (0,5,0), (1,5,-3), (2,5,3), (3,5,-3), (4,5,0) ] ])
]
3.8.12 Paraboloid
Y軸回りの回転で作成される、放物面を記述します。ベースポイント、トップポイントそしてトップの半径で定義されます。
シンタックスは:
Paraboloid (point base, point top, float radius)
baseが放物面のトップを定義します、そしてそれはポイントに来る部分です。
topはサーフェイスの底を定義します、それはそれの幅はそのポイントで半径により定義されます。
放物面定義の例:
Shape [ Paraboloid((0,0,0), (0,3.5,0), 1.5) ]
3.8.13 Parametric surface
u と v の関数で頂点により定義された (スムーズな) 三角形メッシュのそのようなパラメトリックサーフェイスでも生成を可能にします。
それはおのおののメッシュ内のポイントが u と v の関数であることを意味します。
シェイプ修飾指令 ShapeSubdivision (セクション3.9.4) は、どれだけスムーズでそして詳細なサーフェイスでなければならないかを設定するのに有用です。
さらに、シェイプ修飾指令 RenderBound (セクション3.9.2) と共にサーフェイス用に u-v 領域を明示的に定義することによって、サーフェイスの希望の部分だけを作成することが可能です。
シンタックスは:
ParametricSurface ( fx(u,v), fy(u,v), fz(u,v) )
x,y そして z のために u と v について3つの関数を定義します。
通常、常套手段としてはそれぞれの関数に変数を割当て、そして次の例のようにこれらの変数を指令の引数として渡します。
Declare sx = (2/3)*(cos(u)*cos(2*v)+sqrt(2)*sin(u)*cos(v))*cos(u)/(sqrt(2)-sin(2*u)*sin(3*v))
Declare sy = (2/3)*(cos(u)*sin(2*v)-sqrt(2)*sin(u)*sin(v))*cos(u)/(sqrt(2)-sin(2*u)*sin(3*v))
Declare sz = sqrt(2)*cos(u)^2/(sqrt(2)-sin(2*u)*sin(2*v))
Shape [
ParametricSurface(sx, sy, sz)
RenderBound(-PI_TWO, PI_TWO, -PI_TWO, PI_TWO)
ShapeSubdivisions(50, 50, 40)
]
3.8.14 Planar height field (file-based)
ハイトフィールドは、グラフィックスイメージファイル (ファイルベースの高さフィールド) に格納された色値を使うか、あるいは陰関数
(陰関数ハイトフィールドはセクション3.8.7と3.8.8) を使うかによって、頂点の高さが決定したとても小さな三角形のメッシュです。
平面そして球形ハイトフィールドは以下のような何千のシェイプを発生するために使われる事がでます、風景、3Dテキスト、bas-relief
効果、惑星、数学関数 etc.。
平面ファイルベースハイトフィールドのオリジナルの方位は、yとして使用される高さの値と共に1-ユニット幅/1-ユニット長さのbox
(0 <= x <= 1 そして 0 <= z <= 1) 内の、全体のフィールドの方向です。
Shape変形修飾 (セクション3.12) は、その時ハイトフィールドの結果にスケール、回転あるいは移動を使用してしても構いません。
この関係のなかで、縮尺のyの値はy軸のフィールドの高さの調整に使用されます。
データはどのような TGA、JPG、TIF、BMPあるいはPNGフォーマットファイルからでも読み込む事が可能です。
しかしJPGは自然さを失うため、同じソースイメージからは他のフォーマットのほうがより良い結果が得られます。
シンタックスは:
PlanarHeightField string filename
or
PlanarHeightField (string filename, SmoothNormal)
2番目のケースで、SmoothNormal フラグはレンダラにハイトフィールドのために、フィールド内の全てのポイントの法線の計算をさせます。
それは多くの追加メモリの使用を犠牲にして、シェイプのスムーズな外観をもたらします。
filename 引数は単にシェイプを発生させるために使用するイメージファイルを指摘します。
レンダラは自動的に対応するフォーマットタイプを認識するべきです。
平面ハイトフィールド定義の例:
Shape [
PlanarHeightField("hftest.tga", SmoothNormal)
Scale(10, 0.0075, 10)
]
3.8.15 Polygon
VirtuaLight が解釈する凸状 (全ての頂点が全ての他の頂点と、ポリゴンの範囲内収まるラインによって連結する事ができる)
と凹状のポリゴンです。
しかし、両方ともどのような穴も持つ事が出来ず、全ての頂点は同じ平面になければなりません。
追加として、全てのポリゴンの定義に、レンダラはそれを閉じるために、最後の頂点から最初の頂点に辺を付け加えます。
ポリゴンは最小で3つの辺を、最大で32の辺を持たなければなりません。
シンタックスは:、
Polygon (int nvert, point vertices,…)
最初の引数は頂点の正確な数を設定します。
それからカンマで区切られた多角形のそれぞれの頂点定義リストが続きます。
ポイントの総数は nvert と同じでなければなりません。
ポリゴン定義の例:
Shape [ Polygon (3, (552.8, 0.0, 0.0), (0.0, 0.0, 0.0), (0.0, 0.0,
559.2)) ]
3.8.16 Polynomial surface
ワールド座標の限定されたエリア内(Bound指令により指定)で、3つの変数の多項式を評価することにより、どのような任意の代数(多項式)のサーフェイスを生成する事を可能にします。
命令が21以下であるなら、何であっても許可されます。
シンタックスは:
PolynomialSurface (f(x,y,z))
例えば、非常に単純な多項式関数がそうでしょう:
x² + y² + z² - 1 = 0
それは半径が1ユニットで原点が中心の球の定義です。
レンダラにこのシェイプの生成を要求します。
次のように記述しなければなりません。
PolynomialSurface(x^2+y^2+z^2-1.0)
4つの命令の方程式を解くために、 VirtuaLight インタフェースは3つのアルゴリズムを提供します、それは FerrariSolver、VietaSolver、そして
SturmSolver の3つ指令で表されます。
Sturmian シーケンスがデフォルトで使用されます。
ひとつの選択はShape構造体をincludeしなければなりません。
これらの方法のより多くのことについてはセクション3.9.5を参照してください。
多項式サーフェイス定義の例:
Shape [ PolynomialSurface(x^4 + y^4 + z^4 - (x^2 + y^2 + z^2))
Bound((-1.5,-1.5,-1.5), (1.5,1.5,1.5))
VietaSolver
]
3.8.17 Ring
中心、法線、メジャー半径、マイナー半径でリング(中心に穴のある円盤)を記述します。
シンタックスは:
Ring (point center, vector normal, float majrad, float minrad)
centerはディスクの中心を定義し、normalはその方位(それと垂直に交わる方向)を定義し、majradはそのメインの半径を定義し、そしてminradは中心の穴の半径を定義します。
リング定義例:
Shape [ Ring((0,1.5,0), (0,1,-1), 1.5, 0.8) ]
3.8.18 Sphere
中心と半径で完全な球を記述します。
それは VirtuaLight インタフェースによって提供される最も単純でそして最も基本的なシェイプです。
それはレンダリングもまた最速です。
シンタックスは:
Sphere (point center, float radius)
centerの定義はワールド座標中での位置を定義します、そしてradiusは半径を定義します。
radiusは常に正の値で0より大きくなければなりません。
球定義例:
Shape [ Sphere((12,55,-20), sqrt(r1*r2)/2) ]
3.8.19 Spherical height field (file-based)
ハイトフィールドの一般的な定義についてはセクション3.8.13を参照してください。
基本的に球形ハイトフィールドは、サーフェイスの球のベース半径からのオフセットの高さから、ポイントを内部と外部に動かす事により、働きます。
平面のファイルベースハイトフィールドと異なり、球体ハイトフィールドで使用されるイメージファイルは、それが縫い目がなくそして適切に球体を包むように歪められるべきです。
このプリミティブはすでに引数にスケールファクタを持っています、しかしシェイプ変形修飾はハイトフィールドの結果の回転あるいは移動で使用されます。
データは TGA、JPG、TIF、BMPあるいはPNGフォーマットのファイルから読み込み可能です。
しかしJPGは自然さを失うため、同じソースイメージからは他のフォーマットのほうがより良い結果が得られます。
シンタックスは:
SphericalHeightField (float radius, float scale, string filename)
or
SphericalHeightField (float radius, float scale, string filename,
SmoothNormal)
2番目のケースで、SmoothNormal フラグはレンダラにハイトフィールドのために、フィールド内の全てのポイントの法線の計算をさせます。
それは多くの追加メモリの使用を犠牲にして、シェイプのスムーズな外観をもたらします。
最初の引数は球体のベース半径を決定します。
2番目の引数は高さに当てはまるようにスケーリングファクタを設定します。
慣例ではこのファクタは 1/R と記述し、R は最大範囲 (16,32,64,128,256,512,1024のように) を表します。
より大きなRの値はより小さなハイトを生成し、一方より小さな値はより大きなハイトの原因になります。
filename 引数は単にシェイプを発生させるために使用するイメージファイルを指摘します。
レンダラは自動的に対応するフォーマットタイプを認識するべきです。
球体ハイトフィールド定義例:
Shape [ SphericalHeightField(1.25, 1/1024, "shf.tga", SmoothNormal)
]
3.8.20 Superquadric
原点が中心で2つの係数が h と w の、一般化された球を記述します。
superquadricの公式は:
(|x|^(2/w) + |y|^(2/w))^(w/h) + |z|^h - 1.0 = 0
シンタックスは:
Superquadric (float h, float w)
h は上下方向のシェイプ係数で、w は左右方向のシェイプ係数です。
全ての値は正の値で0より大きくなければなりません。
Shape変形修飾 (セクション3.12) はsuperquadricの結果の縮尺、回転あるいは移動で使用するかもしれません。
superquadric 定義の例:
Shape [ Superquadric(3, 3) Translate(0, -1, 2) ]
3.8.21 Surface of revolution
定義された2Dポリゴンを指定された方向について回転させた、レイズ (lathe) サーフェイスを記述します。
このプリミティブは通常、軸に関して対称のシェイプを構築するために使用されます。
陶磁器はそれが回転するとともに、適所に原資料を回し部分を刻んで作ることにより、型のある完全な形が作られる最も有名な例です。
そのどのような回転による閉じたサーフェイスも、ソリッドセット操作で使用する事が可能である事に注意してください。
シンタックスは:
SurfaceOfRevolution (int method, int numpoints, vector dir, { list
of vertices between brackets separated by a comma } )
最初の引数は回転するカーブのタイプを設定します。アーカイブファイル "statics.vib" 内にはおのおのが静的に宣言されています。
STRAIGHT = 1
POLYNOMIAL = 2
CONDITIONAL = 3
STRAIGHT はサーフェイスは単純にラインセグメントを回転させるものであることを意味します。
それは最も速い方法です、しかしそれは鋭角のコーナーに真っ直ぐなエッジを発生させます。
POLYNOMIAL はサーフェイスはラインセグメントに近いスプラインによって表現される事を意味します。
結果は真っ直ぐなエッジや鋭角のコーナーのないスムーズな表現のシェイプになります。
しかし、それは STRAIGHT よりもレンダリングが長く掛かります。
故に、この方法は4番目の多項式の命令を使用するので、3つの指令のうちのひとつ FerrariSolver、VietaSolverそしてSturmSolver
は、ルートsolverで使用するためにShape構造体に含まれて指定されていなければなりません。
デフォルトでは、Vieta の方法が使用されます。
これらにsolverについてもっと知りたい場合はセクション3.9.5を参照してください。
CONDITIONALは、もし頂点がコーナー上になければならないかあるいはカーブから外れることが可能なら、それは可能な限り正確なカーブで使用されます。
2番目の引数は定義されようとしている頂点の正確な数を設定します。
少なくともカーブのための2つのポイントが定義されていなければなりません、しかしたった2つのポイントは単純な円錐形を構築します。
3番目の引数は回転する軸と垂直な平面の法線を定義します。
言い換えれば、それはサーフェイスの回転の方位を設定することです。
例えば、(0,1,0) はy軸に真っ直ぐに上下するレイズ(lathe)サーフェイスのために指定されなければなりません。
それから頂点のリストが続きます。
ポイントはこのような形式で定義されなければなりません:
{x,y}
CONDITIONAL 方法では、ポイント off-curve はこの形式で定義されます:
{0 : x,y} or {OFF : x,y}
そしてポイント on-curve はこの形式で定義されます:
{1 : x,y} or {ON : x,y} or simply {x,y}
Polygon とは異なり、レンダラは自動的にSurfaceOfRevolutionを閉じません。
このシェイプを閉じるこれらの2通りの方法があります:
1)頂点リスト中の開始ポイントと終了ポイントを同じにする。
2)開始ポイントと終了ポイントのx値を0にする、それでそれらは回転の軸上になる。
それをCSG操作 (セクション3.8.23) で使用するために、回転するサーフェイスを閉じることは重要です。
回転サーフェイス定義の例:
Shape [
SurfaceOfRevolution(POLYNOMIAL, 10, (0,1,0),
{0,0}, {1,0.5},
{1.1,1}, {2,1.5},
{2,2}, {2.5,2.5},
{1.1,2}, {1,4},
{0.5,4.5}, {0,4.7} )
SturmSolver
]
3.8.22 Torus
中心、方位、メイジャー半径、マイナー半径でドーナッツシェイプのサーフェイスを記述します。
専門的な話では、torus は、円盤と交差しない平面中の軸についての円盤の回転で生成されます。
故にtorusは4次方程式 (4次多項式) で、3つの指令のうちのひとつ FerrariSolver、VietaSolverそしてSturmSolver
は、ルートsolverで使用するためにShape構造体に含まれて指定されていなければなりません。
デフォルトでは、Vieta の方法が使用されます、それは一般には十分です。
これらにsolverについてもっと知りたい場合はセクション3.9.5を参照してください。
シンタックスは:
Torus (point center, vector dir, float majrad, float minrad)
最初の引数はワールド座標でのtorusの中心位置を決定します。
2番目の引数は回転する円盤に垂直な面の法線を定義します。
このベクトルはサーフェイスの方位を指定します。
3番目の引数はリングの中央の中心位置からの距離を決定します、そしてそれはメイジャー半径です。
最後の引数はリングの半径を設定します、それはマイナーな半径です。
torus定義例:
Shape [ Torus((25,10,-50), (0,1,0), 4, 1) ]
3.8.23 Triangular patch
修飾されたサーフェイス法線ベクタで三角形シェイプを記述します。
このシェイプは三角形を共にブレンドしたグループ、ある意味で個々の三角形の間のシャープなエッジを隠す、を作成するために修飾されたサーフェイス法線ベクタを使用します。
三角形パッチは頂点とその法線のセットにより定義されます。
三角形パッチのためにシェーディング情報が計算された時、スムーズな陰影付けられた三角形を生成するために、法線情報は交点から最終的な法線に自動的に書き換えられるのに使用されます。
通常、CADプログラムあるいは3Dモデラーのような外部ユーティリティは複雑なそしてリアルなオブジェクトを生成するために、多くの数の三角形パッチを作成します。
シンタックスは:
TriangularPatch (point v1, vector n1, point v2, vector n2, point
v3, vector n3)
or
TriangularPatch (point v1, vector n1 UV=uv1,vv1, point v2, vector
n2 UV=uv2,vv2,point v3, vector n3 UV=uv3,vv3)
v1,v2.v3 が三角形の頂点を表します。
n1,n2,n3 が対応する頂点のサーフェイスの法線の方向を表します。
uv1,vv1からuv3,vv3 は対応する頂点の u-v 座標を表します。これらに座標はオプションです。もし省略された場合は以下がセットされます。
uv1 = 0 / vv1 = 0 / uv2 = 1 / vv2 = 0 / uv3 = 0 / vv3 = 1
最終的なオブジェクトを記述するために、Solid構造体として三角形パッチをグループセット化することは普通です。
三角形パッチ定義例:
Shape [ TriangularPatch((209.0679, -67.5589, 107.2871), (0.066,
0.000, -0.998)
UV=0.858,0.226, (209.0679, -84.4554, 107.2871), (-0.066,
0.000, -0.998)
UV=0.858,0.226, (230.0780, -67.5589, 103.1104), (-0.321,
0.000, -0.947)
UV=0.900,0.218) ]
3.8.24 Constructive Solid Geometry
Constructive Solid Geometry (CSG) は、オブジェクトをモデリングする特別の手法です、そしてそれはユニークな体積
(ボリューム) を作成するために、2つあるはより多くのシェイプが論理的に結合されます。
CSGでは全てのオブジェクトは体積を持ちます、なぜならそれらはsolidになるからです。
それらは最早ボリュームを包み込む殻であると考えることは出来ません。
この手法はsolidの内部にあるスペースの区域を類別します、そしてスペースの残りは外側にあります。
CSGでは閉じたシェイプのみを使用する事が重要です、なぜならもしレンダラがシェイプの内側を正確に決定することに困難があれば、結果のsolidは不適切なものになるだろうからです。
複合のsolidオブジェクトは単純なsolidあるいはシェイプのBoolean結合により作成されます。
Boolean演算子は結合したボリュームの新しい内側と外側を定義します。
たとえば球体から3つの小さな円柱を引き算することにより、ボーリングのボールがモデリング可能です。
専門的にはBoolean CSG演算の精巧な階層的ツリーが複雑なCSGオブジェクトを作成します。
VirtuaLight インタフェースは6つConstructive Solid Geometry演算を提供します。
Solidオブジェクトは union (+) 演算子で互いに融合、あるいは merge (^) 演算子で互いにマージ (内部のサーフェイスは取り除かれる融合)
させる事が可能です。
intersection (*) 演算子はオブジェクトの重複する所からシェイプを作成す事が可能です。
オブジェクトはdifference (-) 演算子で他から切り抜くことが可能です。
オブジェクトはclipping (&) 演算子で他を切り取ることが可能です。
最終的に、シェイプの逆数はどのようなBoolean演算でも inverse (~) 演算子で使用可能です。
インターフェイスで、全てのCSG演算はSolid構造体中でなければなりません。
それらはShape構造体 (既に宣言されたか、あるいはSolid構造体中で直接記述された) を on にします、しかし他のSolid構造体にも働く事が可能です。
Solidは他のいかなるシェイプのように見なされなければなりません。
それは同じ物理的なプロパティを取り、容易に変換可能です。
全体のSolid構造体はひとつのシェーダ定義を共用する事が可能です、しかし構造体中に含まれるそれぞれのシェイプはそれ自身のシェーダを持つ事も可能です、そしてそれは親のオブジェクト内のどのテクスチャステートメントでもオーバライドされるでしょう。
言い換えれば、もしSolid構造体でユニークなシェーダの定義が与えられなかった場合は、Solidが得る結果は全てのCGSツリー内部のシェイプのシェーダ定義を保持するでしょう。
これは常に、どのような他のシェイプ修飾定義でも真実です。
続く説明のために、最初の定義はこのような形式の2つのシェイプ A と B であると仮定します。
Declare A = Shape [ … ]
Declare B = Shape [ … ]
与えられた例はとてもシンプルです、しかしインターフェイスは括弧に入れたCGS式を持つことを許します、それでとても複雑なsolidはこのように行う事が可能です。
e.g. A, B, C, D, E そして F は異なるシェイプの定義と仮定します:
Solid [ (A + C) - (B * C + (D ^ E) - (D ^ F)) ]
3.8.24.1 Union
CGSで union は最も単純な演算であり、そして次のイラストによって表されます。
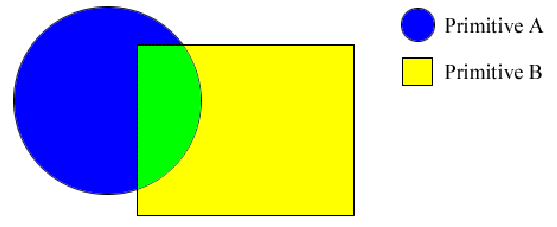
union は2つかそれ以上のシェイプを束ねて、1つのオブジェクト扱う事が出来る1つのエンティティにする単純な接着剤です。
しかしながら、union の内側のサーフェイスは取り除かれません。シェイプが透明なサーフェイスでない限りは問題はありません。
しかし、もしその場合はmerge演算がその代わりに使用されなければなりません。
union演算の最も単純なシンタックスは:
Solid [ A + B ]
3.8.24.2 Merge
このオペレーションは次のイラストによって表されます:
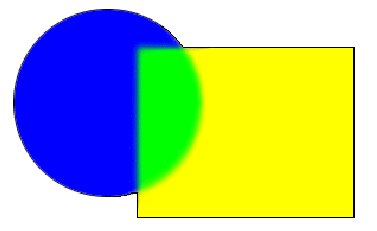
このイラストで、シェイプが重複する黒いエッジは取り除かれます。merge演算はunion と全く同じ働きをしますが、しかし内部のサーフェイスは取り除かれます。
これは特に透明のサーフェイスに役立ちます、なぜならそれは幾何学の内部小片が見える事を避けるからです。
しかしmergeはunionよりも少しだけ遅くなります。
構成要素のシェイプが正確にmergeされるための明確な定義の内側/外側のプロパティを持っていなければならないことは、特に重要です。
merge演算の最も単純なシンタックス:
Solid [A ^ B]
3.8.24.3 Difference
このオペレーションは次のイラストによって表されます:

この例で、シェイプBはシェイプAから引き算されます。
最初のシェイプと全てのサブシーケンスシェイプの inverse のintersection をとる事によってdifference 演算が働きます。
こうしてシェイプ A 内部とシェイプ B 外部のポイントは、両方のシェイプの相違に属する事になります。
もし最初のシェイプが、完全に引き算されたシェイプの内部なら、difference シェイプは見えなくなります。
構成要素のシェイプが正確に引き算されるための明確な定義の内側/外側のプロパティを持っていなければならないことは、特に重要です。
difference 演算の最も単純なシンタックスは:
Solid [A - B]
3.8.24.4 Intersection
このオペレーションは次のイラストによって表されます:

これはシェイプ A とシェイプ B のintersection の結果です、なぜならそれは全ての構成要素が重複するエリアだけを含むsolidを与えるからです。
もしシェイプ A と B の両方で内側なら、ポイントはintersection の一部です。
それはなぜかというと、もし全ての構成要素が重複しなければ、intersection solidは見えなくなるからです。
構成要素のシェイプが正確にintersection されるための明確な定義の内側/外側のプロパティを持っていなければならないことは、特に重要です。
intersection 演算の最も単純なシンタックスは:
Solid [ A * B ]
3.8.24.5 Inverse
CSG演算を実行する時、それの内側を外にするようにシェイプやsolidを裏返す事は有用です。
その出現はレンダラが理解する方法では変える事は出来ません。
inverse 演算が指定された時、シェイプの内側は外側になるようにひっくり返され、逆もまた同じです。
インターフェイスはこの演算を指定するためにシンボル ~ を使用します。
それは裏返すシェイプやsolidより先になければなりません。
例はシェイプ A とinverse されたシェイプ B のintersection です、それは結局のところ A - B です。
Solid [ A * ~B ]
3.8.24.6 Clipping
クリッピング演算子はどのようなシェイプの部分でも切り取るために使用されます。
シェイプ A をシェイプ B によりクリッピングする事は、残っている部分が切り取られて捨てられる一方、シェイプ B の内部にあるシェイプ
A の全ての部分が維持される事を意味します。
そのうえ、この演算は開口部を残します。
clipping 演算子の最も単純なシンタックス:
Solid [ A & B ]



