 |
ここで、分数にまつわる話をしてみようかな。 | ||
| 君たちは、ピタゴラスという人を知っているかな。 | いえ、知らないわ。 |  |
|
| ピタゴラスは、紀元前572年にギリシアの植民地 サモス島に生まれた数学者じゃ。 伝説の上では、音楽家としても知られていた。 そのピタゴラスが、音楽について次のことを 見つけたのじゃ。 |
|||
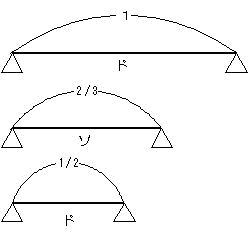
| ある長さの弦(げん)をはって音を出す。 つぎに、その弦の長さを2/3(3分の2)にして 音を出すと、もとの音より5度高い音が出る。 つまり、もとの音をドの音とすると、それより 5度高いソの音が出る。 つぎに、弦の長さをもとの1/2(2分の1) にして音を出すと、こんどはもとの音より8度高い 音が出る。 つまり、もとの音をドの音とすると、それより 1オクターブ高いドの音が出る。 |
|||
 |
へー。そうなのか。 自分でもためして みたいな。 |
 |
|
 |
実はこの後等差数列や調和数列、振動数など というむずかしい考え方を使って、 次のことが言えるのだ。 |
||
| 下のド…1 レ…8/9 ミ…4/5 ファ…3/4 ソ…2/3 ラ…3/5 シ…8/15 上のド…1/2 |
音楽が できるわね。 |
 |
|
| ※ 矢野健太郎「すばらしい数学者たち」 新潮文庫より 原文では、振動数を求めているが、 弦の長さを分数で表すことを具体的にとらえる ために、その逆数をとって表示している。 |