|
�y�@�f�ڃv���O�����@�z |
|
���~������̗��� |
 |
�k�~������̗���l |
|
�����
C�������ɍڂ��Ă���u
�������`���̕\�ʈ��͕��z�v�̊�b�����̈ꕔ�ɓ��Ă͂܂�܂��B
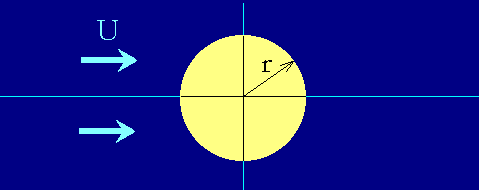
��葬�xU�̈�l������ɒu���ꂽ���ar�̉~������̕��f���x�|�e���V�����́A f=U(z+r2/z)..(1) �ƕ\�����B ���̎��̗���̊��Ղ� ��=Im(f)=U(1-r2/(x2+y2))y ������ł̓Ղ͈��ł��邩��A U(1-r2/(x2+y2))y=C C�͗�����ň��̒萔�ł���A�~���\�ʏ�ł� C=0 �A���̒��ł� C>=0 �ƂȂ�B �㎮��ό`����Bg()�����Ƃ��āA g(x,y;C)=Uy3-Cy2+U(x2-r2)y-Cx2=0 ...(2) �Ƃ���AC ���^����ꂽ���Ax ��ω��������ꍇ�̂��ꂼ���y�̒l�́A(2)���� y �ɂ��ĉ������ɂ���ē�����B ���j���[�g���@ (2)���͂R���������Ȃ̂ŁA�J��Ԃ��v�Z�̓��ӂȃR���s���[�^�̓��������A�j���[�g���@���g�����ߎ��v�Z�ɂ��Ay�̒l�����߂�B �j���[�g���@�͊�f(x)�� f(x)=0 �Ƃ��������������Ƃ��A xi�������̑�i�X�e�b�v�� x �̒l�Ƃ��A���A�����l x0���ݒ肳�ꂽ�Ƃ���A x1,x2,..,xn�́A xi+1=xi-f(xi)/f '(xi) (i=0,1,2,..,n-1) �ŕ\�����Ƃ��o����B������ f '(x)�͔��� df/dx ��\���B n�͖����ɑ����̂ŁA �� x �� |xn-xn-1|<=�� (�Â͏\�������Ȓl) �̎���xn�Ƃ���B ��g(y)=0 ���� y �̒l �ȏ���Q�l��f(x)��g(y)�ɒu��������(2)�����l����B g(x,y;C)��y�ɂ��Ĕ�������A g'=3Uy2-2Cy+U(x2-r2) �j���[�g���@�� yi+1=yi-g(yi)/g'(yi) �Ȃ̂ŁA yi+1=yi-(Uyi3-Cyi2+U(x2-r2)yi-Cx2)/(3Uyi2-2Cyi+U(x2-r2)) ...(3) ������J��Ԃ��B �Ȃ��A�����l�� y0=r �ł悢�B �܂��A���������|yi+1-yi|<=1/10000 �Ƃ���B |
 |
�v���O�����\�[�X���X�g |
|
[flow03.bas] |

 |
�l�@ |
|
�}������Η����͉~�̍ł���Ɖ��ŊԊu���ł������Ȃ��Ă���B���̋����͌����ڂ̒ʂ�A��l����̏ꏊ��1/2�ł���B |
 |
�~���\�ʂ̗���̑��x�x�N�g���ƈ��͕��z |
|
�~������̗�����`��[flow03.bas]����̔��W�ł��B�v���O�������X�g���ɑ�܂��Ȏv�l�̔w�i�������Ă��܂��B�܂��̓��X�g�y�ю��s���ʂ��������育���������B |
�����͕��z�ɂ���
�}���ARe=200000 �Ƃ���̂́A���C�m���Y��Re ��200000 ���Ƃ������ƂŁA�����͎���ɒv���܂��B
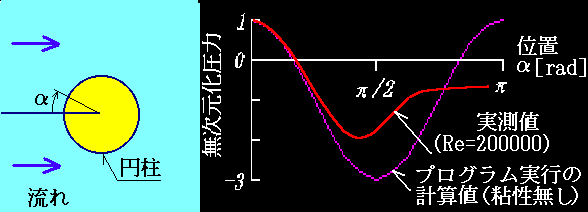
�@�Y��� sin�J�[�u(�����Ȑ��ccos�J�[�u���܂߂��O�p�������Ȑ��̑���)�ɂȂ��Ă���
�A�~���㉺�[�ň��͍͂ŏ��l�����
�B�~���O���ƌ㉏�ň��͍͂ő�l�����c�~�����̂ɂ�鈳�͂̑����͂O�c���S�Ɉ��͂�����
�C�~�����S�c���𒆐S�ɂ��č��E(���̑O��)���Ώ�
�B�͌����Ɩ������A�_�����x�[���̃p���h�b�N�X�ƌĂ����̂ł��B
�܂�A���ۂ͈��͂͑S�ĉ���̂ł͂���܂���B
����͔S���̉e���ŗ��ꂪ���̕\�ʂ��甍����A�Q���������A����̗l�q���w���̏�Ԃ��瘨������ׂł��B
���̗l�q�����͂̒l�ɂ���ăO���t�������̂��A��}�̎����l�̋Ȑ��ł��B
���͎����l���A��S�����̂ɂ��Ẵv���O����[flow031.bas]���s�ɂ��v�Z�l�Ɣ�r����ƁA
�@�~�����̑O�ʂł́A���͂͏�ɁA��荂��
�A�ő�l�͓������A�ŏ��l�́A���傫���c���͍~���̓x������������
�B�~�����̌���ł́A���͉͂����A�Ⴂ�l�̂܂ܐ��ڂ���
�v�Z�l�̂悤�ɗ��ꂪ������Ȃ���Ԃ��A�قڎ����ł��܂����A����͔��ɒx���������A���̂��o�N�e���A���̏����ȕ��������b���A���̓O���Z�����̂悤�� ���ɔS��̂��闬�̂̏ꍇ�ł��B���̗͊w�ŏd�v�Ȗ��������l�̃��C�m���Y�� Re �� 1 ���x�̔��ɒႢ����̏ꍇ�ł��B
�����C�m���Y�� Re
���C�m���Y�� Re ��
Re=Ud/��
=(��\����)�~(��\����)/(���̂̓��S���W��)
�̂��ƂŁA���̂̉^���ɂ��ė��̂̔S���̉e�����ǂꂾ�����������A�����̐��ŕ\�������̂ł��BRe �̑傫���ɂ���ė���̓����͕ω�����̂ŁA���̖ڐ���̖�ڂ����Ă��܂��B
��\����U�Ƒ�\����d�́A���̗��������Â�����̂ł���ARe�̎Z�o�̊�ƂȂ�Ή��ł������̂ŁA�{�v���O�����̂悤�Ɉ�l�����ɗ���ɑ���������𐂒��ɒu�����Î~�~���̏ꍇ�́AU�͈�l���̑����Ad�͉~���̒��a�����̂����ቻ���Ă��܂��B
���̂̓��S���W���˂́A0�`100���ł͉��x�Ƌ��ɉ��~���A���̏ꍇ�A
����15���ł�0.0114cm2/s
����20���ł�0.0100cm2/s
�ł��B
���̈�l����U��40cm/s�A�~���̒��ad��50cm �A����20�� �Ƃ���A���C�m���Y��Re��
Re=Ud/��= 40�~50/0.01=200000
�ŁA�O���t��̎����l�̏ꍇ�Ɉ�v���܂��B
���̃y�[�W�擪��
 |
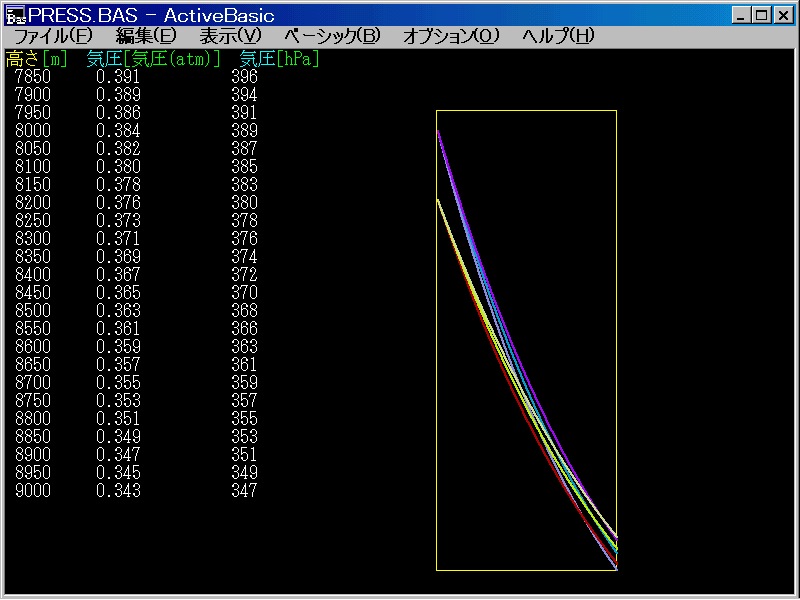
�k���x�ɂ��C���̕ω��l |
|
���͂Ƃ͐�Βl�ł͂Ȃ��A�����ʒu����� |
 |
�v���O�������X�g |
|
[press.bas] |
 |
�k���e�}�l |
|
�����Ō������e�}�Ƃ́A���p���e�}�ł��B���̃T���v���͉����{�^���̂悤�Ȍ`��ł��B�`�����\���ŕ߂炦�A�����̌���
�����s��ɓ��͂���2�̊p�x�A�@��p(�ӂ���=�����낷�p�x)�A�A����(=Z��)���̉�]�p�ŕ\���A���̂悤�ɐݒ肵�����_���猩���鑜��`���܂��B
���C���[�t���[���ƌĂ��`�������g���Ă��܂��B |
 |
�v���O�������X�g |
|
���X�g��210-240�s������ς���A�C�ӂ̕��̂�\���ł���B |
 |
�k���C�t�Q�[���l |
|
���C�t�Q�[���Ƃ́A�V�~�����[�V�����̌ÓT�ł��B |
 |
�v���O�������X�g |
|
[lifegame.bas] (58�s) |
 |
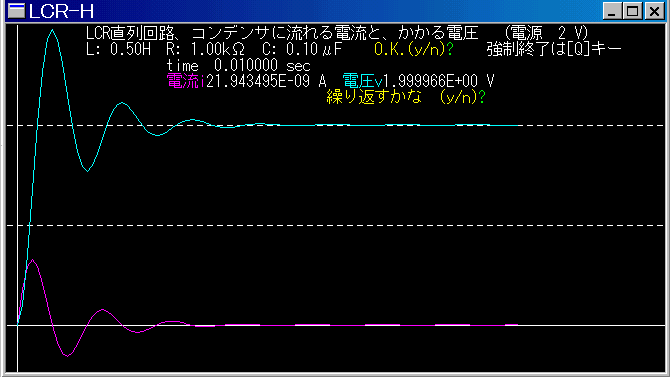
�kLCR�����H�ߓn�����l |
|
|
 |
�E |
|
(a)��P�i�K |
 |
�v���O�������X�g |
|
[ lcr-h.bas ] (80�s) |
 |
�k�X�v���C����ԋȐ��l |
|
�y���@�e�z | |
 |
�y�R���X�v���C�����z |
n �̐ߓ_ |
 |
|
������ c1,d1,bn,dn �͔C�ӂł���B�A���A S(x) ���u���R�ȂR���X�v���C�����v�̎��A |
 |
�y�k�t�����z |
|
�k�t�����Ƃ́A���O�p�s�� �k �� |
 |
�v���O�������X�g |
|
[ Spline.bas ] (�@50�s�@) |
 |
�k�r�����[�h�@�V�~�����[�V���� (Billiards Simulater)�l |
|
|
 |
�v���O�������X�g |
|
[ grgame21.bas ] (188�s) |
 |
�E�E�E�E |
|
1210 H=ABS(A*(X0(I)-X0(K))-G*(Y0(I)-Y0(K)))/SQR(A^2+G^2):' ��ʊ�_�̋O�������ƓI�ʊ�_�Ƃ̋��� |
 |
�E�E�E�E |
|
1940 *HOLE:'---���ɗ��������ǂ������肷��--- |
 |
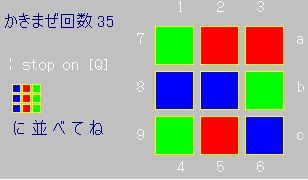
�k���ʃp�Y��33 (Plate Puzzle)�l |
|
���@���s�t�@�C���̓���ɂ��� |
 |
�v���O�������X�g |
|
[ puzzle33.bas ] (77�s) |