四次元図学

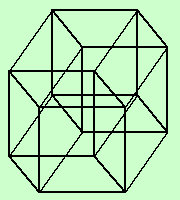
　三次元の立方体はさいころのような形として容易に認識できる。立方体を三次元空間とは垂直の第四の軸方向にぎゅーっと引き伸ばすと四次元超立方体の出来上がり、ということで、私も小学校のころに以下のような図をどこかで見たと思う。

岡田画　(苦笑)

　しかしこれはあんまりな図で、イメージが乏しいばかりか、ほとんど何も情報が得られない(錯視図形としてはよくできているかも)。たとえば超立方体の対角線の長さがルート4、つまり辺の2倍の長さであることは、この図から導き出すことはほとんど不可能であろう。四次元図学で有名な宮崎興二博士の言葉を借りると、
　「(従来の)いずれ(の図)からも正しい距離的あるいは計量的性質は求められず、4次元空間の太陽のもとでは、いかなる陰影が生じ、あるいは遠近感とはどんなものかについての知見も得られない」

　四次元空間は非常に広大であるので、宮崎先生の言う四次元空間の太陽のある風景、は私には正直言って手に余る。
　本稿の目的は、超立方体などの対称四次元図形をきままに収集し、さらにそれをどのように(なるべく豊かなイメージを湧かせる)図として表現するか、である。

2002年8月15日　岡田好一