

正多胞体と半正多胞体の座標計算については、「四次元半正多胞体」の所で引用した文献に詳しく出ている。しかし、その文献はやや手に入りにくいと思えるし、ここで部分的に引用しても唐突には理解しがたいと思われる。
そこで、このページでは三次元の正多面体と左右対称の半正多面体(単純半正多面体)、つまり積正多面体の座標計算をやってみて、半正多胞体の座標計算の準備をすることとしよう。
● メビウスの三角と四面体と…


正多角柱の系列を除くと、半正多面体を構成するための、球面をちょうど一回だけ覆う球面三角形が三種考えられる。それがメビウス三角で、一例を上図(右)に示す。左が元となる正八面体で、中心から外接球に頂点、辺の中点、面の中心点を投影し、最寄の点を球面上で結ぶと、右のようになる。立方体を元にしても全く同じ球面三角形が得られる。これは、正八面体と立方体が双対図形だからである。この正八面体系のメビウス三角は、48枚で球面全体を一回覆う。
同様に、正四面体からは24枚組のメビウス三角が、正二十面体と正十二面体からは120枚組のメビウス三角が得られる。
メビウス球面三角の各頂点の角度は、正四面体系では60°60°90°、正八面体系では45°60°90°、正二十面体系では36°60°90°となっている。
作成の経緯から、メビウス三角の頂点の座標は容易に得られることが分かる。
また、一つのメビウス三角が得られたら、各辺で対する頂点を対称の位置に移せば次のメビウス三角の位置が得られるから、繰り返しによって球面を覆いつくすことも可能である。
ちなみに、四次元では正5胞体、正16胞体、正24胞体、正600胞体から同様の操作で、超球面上の球面四面体が得られる。もちろんメビウス氏が研究したのではないと思うが、本稿では仮にメビウス四面体と呼ぶことにする。五次元には同様の5胞体があり、六次元には同様の超6胞体があり、以下同様である。正n胞体も、正2n胞体も、正24胞体も、正600胞体もその頂点座標が計算できるから、メビウス四面体などの座標も容易に計算可能である。
頂点を対する面や体などに対して対称点に移す操作も後のほうで述べる外積操作を知っていれば、難しくはない。
● 半正多面体の作成
メビウス三角の座標が求まれば、その頂点、辺上の対角二等分点、内心を求め、辺で折り返してゆけば正多面体や単純半正多面体が得られる。注意点は、内心等を求める際は球面上での角度を考えるのであって、三次元空間内でのまっすぐな直線で似たような操作をしても位置がずれてしまう。しかしもちろん、正多面体などの図形を描くときの頂点を結ぶ直線や平面は真っ直ぐであって、球面上に乗らない。
ということで、これまで私はずっと、メビウス三角の隣り合う辺を延長して大円を描き、大円が乗っている面の角度の平均を取って対角二等分点や内心を計算していた。
ところが、「四次元半正多胞体」の所で引用した文献にはずっと簡単な角度二分法があり、驚くことに四次元以上にも、その計算法が応用できるのである。私はこの計算法が著者の石井氏のオリジナルかどうかを知らない。とにかく、以下には私の理解したことを述べさせていただく。
● 球面三角の内心等の座標計算
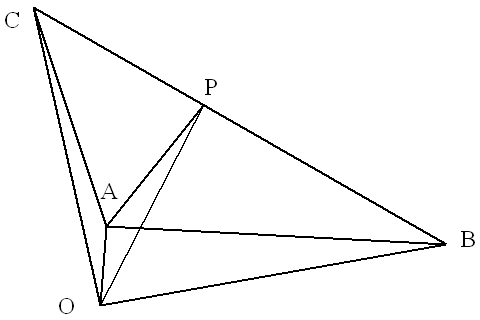
下図で説明する。△ABCがメビウス三角(球面三角形)の頂点を直線で結んだ平らな三角形と考えて欲しい。点Oは図形の中心である。点Pはメビウス三角の辺BCの対角二等分点に射影される点とする。つまり、△OABと△OAPのなす角と△OACと△OAPのなす角が等しいとする。問題は、点O、点A、点B、点Cの座標が分かっている場合に、点Pの座標がどのように計算できるか、である。一般の場合、辺AB、辺BC、辺CAの長さはすべて異なる。
OA、OB、OCの長さは円の半径に等しいのだが、等しさは以下の計算には役立たない。
なお、半正多面体などの図形を描く際には点Pの座標が直接得られなくとも、点Oからの方向が分かれば良いことに注意。
辺BPの長さをsとし、辺CPの長さをtとすると、点Pは直線BC上にあるのだから、点Pの座標はベクトル(O→B)とベクトル(O→C)を使って、以下のように表すことができる。
(O→P) = (t/(s + t))(O→B) + (s/(s + t))(O→C)
驚くことに、
s : t = (△OABの面積) : (△OACの面積)
になっている。その証明は以下の通り。
s : t = (四面体OABPの体積) : (四面体OACPの体積)
というのも、2つの四面体は△OAPを共有しており、点B、点C、点Pは同一直線上にあるからである。
△OABと△OAPのなす角と△OACと△OAPのなす角が等しい、
ので、
点Pから△OABと△OACに下ろした垂線(図には描かれていない)の長さは等しい。
(∵△OAPを含む平面の任意の点から△OABの平面と△OACの平面に下ろした垂線の長さは等しい)
角錐の体積は、1/3×底面積×高さ、
なので、高さが等しいのだから、
(△OABの面積) : (△OACの面積) = (四面体OABPの体積) : (四面体OACPの体積)
ということになる。
以上が納得できると、メビウス三角の内心も簡単に算出できる。
△OABの面積をN、△OBCの面積をL、△OCAの面積をM、
とし、メビウス三角(球面三角)の内心に投影される△ABC上の点をQとすると、
(O→Q) = (L/(L+M+N))(O→A) + (M/(L+M+N))(O→B)
+ (N/(L+M+N))(O→C)
ベクトル(O→Q)の長さを半径に延ばせば、その点がメビウス三角の内心になっている。
(蛇足だが、点Qは△ABC平面上の点だが、一般には△ABCの内心ではない)
△OAB等の面積は、外積(×)を用いて容易に計算できる。
△OABの面積 = (1/2)|(O→A)×(O→B)| ただし、|v|はベクトルvの大きさ(=長さ)
外積の計算法については下の具体例を参照。
以上をまとめると、メビウス三角の頂点座標が分かれば内心等の半正多面体に必要な座標が上記の方法で計算できる、ということになる。
びっくりするのは、この算出法が任意の高次元に拡張できることである。
たとえば四次元では、メビウス四面体ABCDを考え、面積ではなく体積OABC等を考える。ベクトル(O→A)と体積OBCD(スカラ値)の積(ベクトル)などをベクトルの足し算すると、メビウス四面体の超内心等の座標が得られる。その具体的方法は、この文章を読んでいただいているみなさんの想像の範囲とは思うが、別のページで改めて解説したい。
三次元に話を戻そう。
![]()
● 三次元での半正多面体の頂点座標の具体的求め方
八面体系のメビウス三角の3つの頂点の座標は、たとえば、
A:(1, 0, 0), B:(1/sqrt(2), 1/sqrt(2), 0), C:(1/sqrt(3), 1/sqrt(3), 1/sqrt(3))
などとなる。半径1の球面三角形だから、単位球面に張り付いている。
中心点はO(0, 0, 0)である。だから、ベクトル(O→A)、(O→B)、(O→C)も同じく、
(O→A):(1, 0, 0), (O→B):(1/sqrt(2), 1/sqrt(2),
0), (O→C):(1/sqrt(3), 1/sqrt(3), 1/sqrt(3))
と表すことができる。
計算を一般化するため、以下、
A:(xa, ya, za), B:(xb, yb, zb), C:(xc, yc, zc)
と、座標等を記号で表す。
ベクトルの外積(×)は、
(O→A)×(O→B) = (ya*zb-za*yb, za*xb-xa*zb, xa*yb-ya*xb)
(O→B)×(O→C) = (yb*zc-zb*yc, zb*xc-xb*zc, xb*yc-yb*xc)
(O→C)×(O→A) = (yc*za-zc*ya, zc*xa-xc*za, xc*ya-yc*xa)
である。行列式を知っている方には、行列式で書いた方が分かりやすいと思う。
この外積(ベクトル)の方向は、元の2つのベクトルに垂直で、大きさは2つのベクトルで表される平行四辺形の面積である。
したがって、△OABの面積(スカラ)は、
▲OAB = (1/2)*|(O→A)×(O→B)| = (1/2)*sqrt((ya*zb-za*yb)2+(za*xb-xa*zb)2+(xa*yb-ya*xb)2)
▲OABという三角形の面積の書き表し方は珍しいと思うが、文字数の節約のため、以下、用いる。
当然、▲OBCと▲OCAも同様に計算できる。
半正多面体の座標の素材となるベクトルは、
TA = ▲OBC * (O→A) = (▲OBC * xa, ▲OBC * ya, ▲OBC * za) = (xta,
yta, zta)
TB = ▲OCA * (O→B) = (▲OCA * xb, ▲OCA * yb, ▲OCA * zb) = (xtb,
ytb, ztb)
TC = ▲OAB * (O→C) = (▲OAB * xc, ▲OAB * yc, ▲OAB * zc) = (xtc,
ytc, ztc)
最後のxta等は、以下の計算で用いるための記号である。xta = ▲OBC * xaなどのことである。
さて、八面体系の球面三角形(メビウス三角)ABCの∠Aは45°、∠Bは90°、∠Cは60°である。
元々の(O→A)を素直に使っても良いのだが、TAを用いてもよい。48のメビウス三角について、TAの点を打ち、隣り合うメビウス三角上の他のTA点をつないで辺にすると、TAからは正八面体が得られる。同様にして、
TA 正八面体
TB 立方八面体
TC 立方体
次に、TA + TB = (xta+xtb, yta+ytb, zta+ztb)などの点を使うと、
TA+TB 切頭八面体
TB+TC 切頭立方体
TC+TA 斜方立方八面体
最後に、TA + TB + TC = (xta+xtb+xtc, yta+ytb+ytc, zta+ztb+ztc)の点を使うと、
TA+TB+TC 斜方切頭立方八面体
が得られる。
外接球の半径を1に揃えるのなら、各ベクトルの大きさで割ればよい。たとえば、TA+TBだと、
d = sqrt((xta+xtb)2+(yta+ytb)2+(zta+ztb)2) これが大きさ(長さ)
(TA+TB)' = ((xta+xtb)/d, (yta+ytb)/d, (zta+ztb)/d)
と計算し、最後の(xta+xtb)/dなどの数値を使う。
![]()
● おまけ。メビウス三角の計算機内での折り返し方
メビウス三角ABCを辺BCで折り返した、隣のメビウス三角A'BCの点A'を求めてみよう。
座標は、点A:(xa, ya, za)、点B:(xb, yb, zb)、点C:(xc, yc, zc) とする。
面OBCの法線ベクトル、つまり(平らな)三角形OBCを含む平面に垂直なベクトルは、外積によって得られる。
(O→B)×(O→C) = (yb*zc-zb*yc, zb*xc-xb*zc, xb*yc-yb*xc)
大きさを1にするため、ベクトルの大きさ、
d2 = sqrt((yb*zc-zb*yc)2+(zb*xc-xb*zc)2+(xb*yc-yb*xc)2)
で各要素を割る。
NBC:(xn, yn, zn) = ((yb*zc-zb*yc)/d2, (zb*xc-xb*zc)/d2, (xb*yc-yb*xc)/d2)
法線ベクトルと元のベクトルの内積(・)をとって、法線ベクトル方向の距離を出す。
d3 = (O→A)・NBC = xa*xn+ya*yn+za*zn
A'は法線ベクトルの反対方向に、2倍の変位の位置にあるから、
A' = (xa-2*d3*xn, ya-2*d3*yn, za-2*d3*zn)
同様の操作を各辺に対して次々に新しいメビウス三角に対しても行うと、球面はメビウス三角で覆い尽くされる。
![]()
(以下、なんだか冗長な気もするのだが、他に機会もないので残しておく)
● おまけ、その2。斜交座標の利用
メビウス三角のセットが得られたら、上述のTA+TB等を三角一つずつに対して算出しても間違いではないが、最初のメビウス三角ABCで得られたTA+TB等の点Pを元に、以下のka,
kb, kcを算出しておいて、
P':(xp1, yp1, zp1) = ka*A' + kb*B' + kc*C' つまり、
xp1 =
ka*xa1+kb*xb1+kc*xc1
yp1 = ka*ya1+kb*yb1+kc*yc1
zp1 =
ka*za1+kb*zb1+kc*zc1
みたいに、別のメビウス三角A'B'C'から簡単に座標P'が計算できれば(計算機が)楽である。この計算式を素直にながめると、OA'とOB'とOC'が座標軸のように見えるのだが、互いに直交してはいないので、斜交座標と考えられる。
要は、三元連立方程式であるので、行列式を用いれば良いのだが、以下に直感的な方法を紹介する。
前提として、
xp = ka*xa+kb*xb+kc*xc
yp = ka*ya+kb*yb+kc*yc
zp =
ka*za+kb*zb+kc*zc
の各点(P, A, B, C)が得られていて、ka, kb, kcを算出する。原点O, A, B,
Cの四点は同一平面上にないものとする。
点Pの平面OABからの距離の成分は、kcが担当しているはずである。そのため、例によって、OABの法線ベクトルを算出する。
(O→A)×(O→B)
= (ya*zb-za*yb, za*xb-xa*zb, xa*yb-ya*xb) だから、
xn2 = ya*zb-za*yb, yn2 =
za*xb-xa*zb, zn2 =
xa*yb-ya*xb と計算しておく。
kcは、P成分とC成分の比であるので、内積の比を取ればよい。
kc =
(xp*xn2+yp*yn2+zp*zn2)/(xc*xn2+yc*yn2+zc*zn2)
(結局、三元連立方程式を素直に解いたのと等価である^_^;)
得られたkcを使って、点PをOAB平面に移す。
xp2
= xp - kc*xc (= ka*xa+kb*xb)
yp2 = yp - kc*yc (= ka*ya+kb*yb)
zp2 = zp
- kc*zc (= ka*za+kb*zb)
同様に内積を使ってkbの値を出そう。
まず、OAに垂直でOAとOBで決まる平面上のベクトルは、
B" = B -
(EA・B)EA シュミットの直交化法(EAはベクトルAを単位化したもの)
da =
sqrt(xa2+ya2+za2)
xea = xa/da, yea =
ya/da, zea = za/da
ただし、通常、メビウス三角は半径1の球面にいるので、AとEAは同じであるが…。
ieab =
xea*xb+yea*yb+zea*zb
xb2 = xb-ieab*xea, yb2 = yb-ieab*yea, zb2 =
zb-ieab*zea
(kcの時と同様に) kbはP"成分とB成分の比である。
kb =
(xp2*xb2+yp2*yb2+zp2*zb2)/(xb*xb2+yb*yb2+zb*zb2)
最後に、kaを出す。kbを使って、点Pをさらに直線OA上に持ってくる。
xp3 = xp2 - kb*xb (=
ka*xa)
yp3 = yp2 - kb*yb (= ka*ya)
zp3 = zp2 - kb*zb (=
ka*za)
kaはA成分との比を取ればよい。
ka =
(xp3*xa+yp3*ya+zp3*za)/(xa*xa+ya*ya+za*za)
2002年10月19日 岡田好一