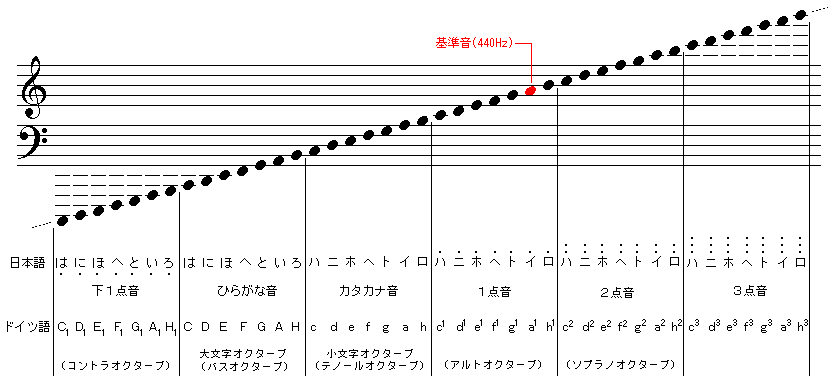
| 壒柤 | 僪 | 僪侐乮儗侒乯 | 儗 | 儗侐乮儈侒乯 | 儈 | 僼傽 | 僼傽侐乮僜侒乯 | 僜 | 僜侐乮儔侒乯 | 儔 | 儔侐乮僔侒乯 | 僔 |
| 擔杮岅 | 僴乮塪儘乯 | 塪僴乮曄僯乯 | 僯 | 塪僯乮曄儂乯 | 儂乮曄傊乯 | 僿乮塪儂乯 | 塪傊乮曄僩乯 | 僩 | 塪僩乮曄僀乯 | 僀 | 塪僀乮曄儘乯 | 儘乮曄僴乯 |
| 侐侐 | 丂 | 廳塪儘 | 廳塪僴 | 丂 | 廳塪僯 | 丂 | 廳塪儂 | 廳塪僿 | 丂 | 廳塪僩 | 丂 | 廳塪僀 |
| 侒侒 | 廳曄僯 | 丂 | 廳曄儂 | 廳曄僿 | 丂 | 廳曄僩 | 丂 | 廳曄僀 | 丂 | 廳曄儘 | 廳曄僴 | 丂 |
| 僪僀僣岅 | 俠 乮俫倝倱乯 |
俠倝倱 乮俢倕倱乯 |
俢 | 俢倝倱 乮俤倱乯 |
俤 乮俥倕倱乯 |
俥 乮俤倝倱乯 |
俥倝倱 乮俧倕倱乯 |
俧 | 俧倝倱 乮俙倱乯 |
俙 | 俙倝倱 乮俛乯 |
俫 乮俠倕倱乯 |
| 侐侐 | 丂 | 俫倝倱倝倱 | 俠倝倱倝倱 | 丂 | 俢倝倱倝倱 | 丂 | 俤倝倱倝倱 | 俥倝倱倝倱 | 丂 | 俧倝倱倝倱 | 丂 | 俙倝倱倝倱 |
| 侒侒 | 俢倕倱倕倱 | 丂 | 俤倱倕倱 | 俥倕倱倕倱 | 丂 | 俧倕倱倕倱 | 丂 | 俙倱倕倱 俙倱倎倱 |
丂 | 俛倕倱 俛俛 俫倕倱倕倱 |
俠倕倱倕倱 | 丂 |
| 擔杮岅 | 僪僀僣岅 | 僀僞儕傾岅 | 僼儔儞僗岅 | 塸岅 |
| 僴 僯 儂 僿 僩 僀 儘 |
俠丗僣僃乕 俢丗僨乕 俤丗僄乕 俥丗僄僼 俧丗僎乕 俙丗傾乕 俫丗僴乕 |
俢倧 俼倕 俵倝 俥倎 俽倧倢 俴倎 俽倝 |
俢倧乮倀倲乯 俼倕 俵倝 俥倎 俽倧倢 俴倎 俽倝 |
俠 俢 俤 俥 俧 俙 俛 |
| 侐 | 侐 | 侐 | 侐 | 侐 |
| 塪僴 塪僯 塪儂 塪僿 塪僩 塪僀 塪儘 |
俠倝倱丗僣傿僗 俢倝倱丗僨傿僗 俤倝倱丗僄僀僗 俥倝倱丗僼傿僗 俧倝倱丗僊僗 俙倝倱丗傾僀僗 俫倝倱丗僸僗 |
俢倧丂倓倝倕倱倝倱 俼倕丂倓倝倕倱倝倱 俵倝丂倓倝倕倱倝倱 俥倎丂倓倝倕倱倝倱 俽倧倢丂倓倝倕倱倝倱 俴倎丂倓倝倕倱倝倱 俽倝丂倓倝倕倱倝倱 |
俢倧乮倀倲乯丂倓倝倕倱倕 俼倕丂倓倝倕倱倕 俵倝丂倓倝倕倱倕 俥倎丂倓倝倕倱倕 俽倧倢丂倓倝倕倱倕 俴倎丂倓倝倕倱倕 俽倝丂倓倝倕倱倕 |
俠丂倱倛倎倰倫 俢丂倱倛倎倰倫 俤丂倱倛倎倰倫 俥丂倱倛倎倰倫 俧丂倱倛倎倰倫 俙丂倱倛倎倰倫 俛丂倱倛倎倰倫 |
| 侒 | 侒 | 侒 | 侒 | 侒 |
| 曄僴 曄僯 曄儂 曄僿 曄僩 曄僀 曄儘 |
俠倕倱丗僣僃僗 俢倕倱丗僨僗 俤倱丗僄僗 俥倕倱丗僼僃僗 俧倕倱丗僎僗 俙倱丗傾僗 俛丗傋乕 |
俢倧丂倐倕倣倧倢倢倕 俼倕丂倐倕倣倧倢倢倕 俵倝丂倐倕倣倧倢倢倕 俥倎丂倐倕倣倧倢倢倕 俽倧倢丂倐倕倣倧倢倢倕 俴倎丂倐倕倣倧倢倢倕 俽倝丂倐倕倣倧倢倢倕 |
俢倧乮倀倲乯丂倐倕倣倧倢倕 俼倕丂倐倕倣倧倢倕 俵倝丂倐倕倣倧倢倕 俥倎丂倐倕倣倧倢倕 俽倧倢丂倐倕倣倧倢倕 俴倎丂倐倕倣倧倢倕 俽倝丂倐倕倣倧倢倕 |
俠丂倖倢倎倲 俢丂倖倢倎倲 俤丂倖倢倎倲 俥丂倖倢倎倲 俧丂倖倢倎倲 俙丂倖倢倎倲 俛丂倖倢倎倲 |
| 侐侐 | 侐侐 | 侐侐 | 侐侐 | 侐侐 |
| 廳塪僴 廳塪僯 廳塪儂 廳塪僿 廳塪僩 廳塪僀 廳塪儘 |
俠倝倱倝倱丗僣傿僔僗 俢倝倱倝倱丗僨傿僔僗 俤倝倱倝倱丗僄僀僔僗 俥倝倱倝倱丗僼傿僔僗 俧倝倱倝倱丗僊僔僗 俙倝倱倝倱丗傾僀僔僗 俫倝倱倝倱丗僸僔僗 |
俢倧丂倓倧倫倫倝倧丂倓倝倕倱倝倱 俼倕丂倓倧倫倫倝倧丂倓倝倕倱倝倱 俵倝丂倓倧倫倫倝倧丂倓倝倕倱倝倱 俥倎丂倓倧倫倫倝倧丂倓倝倕倱倝倱 俽倧倢丂倓倧倫倫倝倧丂倓倝倕倱倝倱 倢倎丂倓倧倫倫倝倧丂倓倝倕倱倝倱 俽倝丂倓倧倫倫倝倧丂倓倝倕倱倝倱 |
俢倧乮倀倲乯丂倓倧倳倐倢倕丂倓倝倕倱倕 俼倕丂倓倧倳倐倢倕丂倓倝倕倱倕 俵倝丂倓倧倳倐倢倕丂倓倝倕倱倕 俥倎丂倓倧倳倐倢倕丂倓倝倕倱倕 俽倧倢丂倓倧倳倐倢倕丂倓倝倕倱倕 倢倎丂倓倧倳倐倢倕丂倓倝倕倱倕 俽倝丂倓倧倳倐倢倕丂倓倝倕倱倕 |
俠丂倓倧倳倐倢倕丂倱倛倎倰倫 俢丂倓倧倳倐倢倕丂倱倛倎倰倫 俤丂倓倧倳倐倢倕丂倱倛倎倰倫 俥丂倓倧倳倐倢倕丂倱倛倎倰倫 俧丂倓倧倳倐倢倕丂倱倛倎倰倫 俙丂倓倧倳倐倢倕丂倱倛倎倰倫 俛丂倓倧倳倐倢倕丂倱倛倎倰倫 |
| 侒侒 | 侒侒 | 侒侒 | 侒侒 | 侒侒 |
| 廳曄僴 廳曄僯 廳曄儂 廳曄僿 廳曄僩 廳曄僀 廳曄儘 |
俠倕倱倕倱丗僣僃僙僗 俢倕倱倕倱丗僨僙僗 俤倱倕倱丗僄僙僗 俥倕倱倕倱丗僼僃僙僗 俧倕倱倕倱丗僎僙僗 俙倱倕倱丗傾僙僗(俙倱倎倱丗傾僒僗) 俫倕倱倕倱丗僿僙僗(俛倕倱丗傋僗,俛俛丗傋乕傋乕) |
俢倧丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俼倕丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俵倝丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俥倎丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俽倧倢丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俴倎丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 俽倝丂倓倧倫倫倝倧丂倐倕倣倧倢倢倕 | 俢倧乮倀倲乯丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俼倕丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俵倝丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俥倎丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俽倧倢丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俴倎丂倓倧倳倐倢倕丂倐倕倣倧倢倕 俽倝丂倓倧倳倐倢倕丂倐倕倣倧倢倕 |
俠丂倓倧倳倐倢倕丂倖倢倎倲 俢丂倓倧倳倐倢倕丂倖倢倎倲 俤丂倓倧倳倐倢倕丂倖倢倎倲 俥丂倓倧倳倐倢倕丂倖倢倎倲 俧丂倓倧倳倐倢倕丂倖倢倎倲 俙丂倓倧倳倐倢倕丂倖倢倎倲 俛丂倓倧倳倐倢倕丂倖倢倎倲 |
 |
| 仸椺偊偽侾僆僋僞乕僽偼侾丗俀偺斾棪偵側傞偨傔婎弨壒乮係係侽俫倸乯 偺侾僆僋僞乕僽壓偼丂俀俀侽俫倸丂偵側傝丄侾僆僋僞乕僽忋偑丂俉俉侽俫倸丂偵側傝傑偡丅 |
| 椺偊偽 弮惓俆搙乮俀丗俁乯傪侾俀夞愊傒廳偹偨応崌偲姰慡俉搙乮侾丗俀乯傪俈夞愊傒廳偹偨応崌偱斾妑偟偰傒傞偲丅 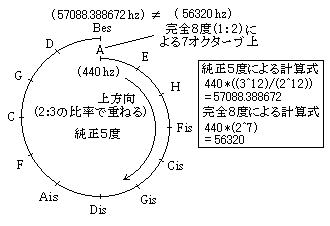 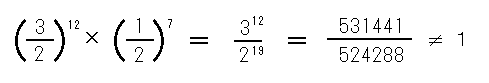 偺幃偐傜傕堦抳偟側偄偙偲偑傢偐傝丄偙偺壒掱嵎傪乽僺僞僑儔僗丒僐儞儅乿偲偄偄傑偡丅 |
| 僴壒傪婎弨偲偡傞壒棩斾妑昞乮壒妝帿揟傛傝乯 | 乮扨埵僙儞僩乯 | |||||||||||
| 僴 | 塪僴丒曄僯 | 僯 | 塪僯丒曄儂 | 儂 | 僿 | 塪僿丒曄僩 | 僩 | 塪僩丒曄僀 | 僀 | 塪僀丒曄儘 | 儘 | |
| 乲僺儏僞僑儔僗壒棩宯乴 | ||||||||||||
| 侾丏僺儏僞僑儔僗壒棩 | 0 |
114 |
204 |
294 |
408 |
498 |
612 |
702 |
816 |
906 |
996 |
1110 |
| 俀丏僌儔儞儅僥僂僗 乮姴壒僺儏僞僑儔僗壒棩偵傛傞偑攈惗壒偼慡壒傪摍暘偟偰媮傔傞乯 |
0 |
102 |
204 |
306 |
408 |
498 |
600 |
702 |
804 |
906 |
1008 |
1110 |
| 乲弮惓棩宯乴 | ||||||||||||
| 俁丏弮惓棩 | 0 |
92 |
204 |
316 |
386 |
498 |
590 |
702 |
773 |
884 |
996 |
1088 |
| 係丏儔儌僗丒僨丒僷儗僴 | 0 |
92 |
182 |
294 |
386 |
498 |
590 |
702 |
792 |
884 |
996 |
1088 |
| 俆丏働僾儔乕 | 0 |
92 |
204 |
316 |
386 |
498 |
590 |
702 |
794 |
906 |
1018 |
1088 |
| 乲拞慡壒棩宯乴 | ||||||||||||
| 俇丏傾乕儘儞乮侾乛係僐儞儅乯 | 0 |
76 |
193 |
310 |
386 |
503 |
579 |
697 |
773 |
890 |
1007 |
1083 |
| 俈丏僣傽儖儕乕僲乮俀乛俈僐儞儅乯 | 0 |
70 |
191 |
313 |
383 |
504 |
574 |
696 |
817 |
887 |
1008 |
1078 |
| 俉丏僉儖儞儀儖僈乕乮曄懃揑侾乛俀僐儞儅乯 | 0 |
90 |
204 |
294 |
386 |
498 |
590 |
702 |
792 |
895 |
996 |
1088 |
| 俋丏俙丏償僃儖僋儅僀僗僞乕乮戞嘨丅曄懃揑侾乛係僐儞儅乯 | 0 |
96 |
204 |
300 |
396 |
504 |
600 |
702 |
792 |
900 |
1002 |
1098 |
| 侾侽丏儅乕儖僾儖僋乮侾乛侾侽僐儞儅乯 | 0 |
99 |
200 |
301 |
399 |
500 |
599 |
700 |
798 |
899 |
1000 |
1099 |
| 乲侾俀暯嬒棩宯乴 | ||||||||||||
| 侾侾丏棟榑抣 | 0 |
100 |
200 |
300 |
400 |
500 |
600 |
700 |
800 |
900 |
1000 |
1100 |
| 侾俀丏僈儕儗僀乮敿壒傪侾俉丗侾俈偵偲偭偨傕偺乯 | 0 |
99.0 |
197.9 |
296.9 |
395.8 |
494.8 |
593.7 |
692.7 |
791.6 |
890.6 |
989.5 |
1088.5 |
| 侾俁丏儊儖僙儞僰乮婔壗妛揑偵媮傔偨暯嬒棩乯 | 0 |
100.4 |
200.9 |
301.3 |
401.8 |
501.6 |
601.3 |
701.1 |
800.9 |
900.6 |
1000.4 |
1100.2 |
| 侾係丏僗僥僼傿乕儞乮侾俀併俀偵傛傞暯嬒棩乯 | 0 |
99.7 |
199.6 |
300.2 |
400.0 |
499.6 |
600.0 |
699.8 |
799.6 |
900.3 |
1000.1 |
1099.7 |
| 侾俆丏僼傽僂儖僴乕僶乕乮懳悢傪梡偄偨偲峫偊傜傟傞暯嬒棩乯 | 0 |
100.0 |
200.1 |
300.1 |
400.0 |
500.0 |
600.1 |
700.2 |
800.2 |
900.2 |
1000.1 |
1100.1 |
| 侾俇丏俴丏僴儌儞僪乮僴儌儞僪丒僆儖僈儞偵梡偄傜傟偨暯嬒棩乯 | 0 |
100.7 |
200.0 |
300.0 |
400.7 |
500.4 |
600.1 |
699.8 |
800.7 |
900.6 |
1000.6 |
1100.3 |
| 弌揟偼埲壓偵偵傛傞丅 俀丏俫丏俧倰倎倣倣倎倲倕倳倱亙俙値倷丂値倕倵丂倠倳値倱倲倢倝們倛丂俛倳倕們倛亜乮侾俆侾俉乯 係丏俛丏俼倎倣倧倱丂倓倕丂俹倎倰倕倞倎亙俵倳倱倝們倎丂俹倰倎們倲倝們倎亜乮侾係俉俀乯 俆丏俰丏俲倕倫倢倕倰亙俫倎倰倣倧値倝們倕倱丂倣倳値倓倝亜乮侾俇侾俋乯 俇丏俹丏俙倎倰倧値丂亙俿倧倱們倎値倕倢倢倧丂in丂倣倳倱倝們倎亜乮侾俆俀俋乯 俈丏俧丏倅倎倰倢倝値倧亙俴倕丂倝倱倲倝倲倳倲倝倧値倝丂倛倎倰倣倧値倝們倛倕亜乮侾俆俆俉乯 俉丏俰丏俹丏俲倝倰値倐倕倰倗倕倰亙俢倝倕丂俲倳値倱倲丂倓倕倱丂倰倕倝値倕値丂俽倎倲倸倕倱丂倝値丂倓倕倰丂俵倳倱倝倠亜乮侾俈俈俋乯 俋丏俙丏倂倕倰們倠倣倕倝倱倲倕倰亙俵倳倱倝們倎倢倝倱們倛倕丂俿倕倣倫倕倰倎倲倳倰亜乮戞俀斉丆侾俇俋侾乯 侾侽丏俥丏倂丏俵倎倰倫倳倰倗亙倁倕倰倱倳們倛丂倀倐倕倰丂倓倝倕丂倣倳倱倝倠倎倢倝倱們倛倕丂俿倕倣倫倕倰倎倲倳倰亜乮侾俈俈俇乯 侾俀丏倁丏俧倎倢倝倢倕倝亙俢倝倎倢倧倗倧丂倓倕倢倢倎丂倣倳倱倝們倎丂倎値倲倝們倎丂倕倲丂倓倕倢倢倎丂倣倧倓倕倰値倎亜乮侾俆俉侾乯 侾俁丏俵丏俵倕倰倱倕値値倕亙俫倎倰倣倧値倝倕丂倳値倝倴倕倰倱倕倢倢倕亜乮侾俇俁俇乣俁俈乯 俽丏俽倲倕倴倝値亙倁倎値丂倓倕丂倱倫倝倕倗倕倢倝値倗丂倓倕倰丂倱倝値倗們倧値倱倲亜乮們倎丏侾俇侽侽乯 侾俆丏俰丏俥倎倳倢倛倎倐倕倰亙俬値倗倕値倝倕倳倱亅俽們倛倳倢亜乮侾俇俁侽乯 侾俇丏俴丏俫倎倣倣倧倣倓丗倀値倝倲倕倓丂俽倲倎倲倕倱丂俹倎倲倕値倲丆侾俋俆俇俁俆侽乮侾俋俁係乯 侾俋悽婭偵側偭偰俆俁暯嬒棩偲侾侾俉暯嬒棩傪旕忢偵崅偔昡壙偟偨儃乕僓儞働僢僩乮俼丏俫丏俛倧倱倎値倯倳倕倲乯偑侾俉俈俇擭偵俆俁暯嬒棩傪梡偄偰僆僋僞乕僽偵俆俁偺尞斦傪傕偮妝婍傪奐敪偟偨丅 偙傟偼弮惓偵旕忢偵嬤偄壒棩偑弌偣傞偑墘憈崲擄偱丆棟榑揑側妝婍偲偟偰廔傢偭偨丅 |
||||||||||||
| 忋弎偺僙儞僩偵偮偄偰乮壒妝帿揟偐傜偺堷梡乯 ------------------------------------------------------------ 僙儞僩 僄儕僗偵傛偭偰峫埬偝傟偨壒掱偺悢妛揑昞帵朄偺扨埵丅壒妝壒嬁妛傗斾妑壒妝妛傪偼偠傔懡偔偺暘栰偱丄崙嵺揑丄堦斒揑偵巊梡偝傟偰傞丅 暯嬒棪偺敿壒傪侾侽侽摍暘偟偨棟榑忋偺壒掱傪丄侾僙儞僩乮們倕値倲傑偨偼俠乯偲偟偨傕偺丄敿壒偼侾侽侽僙儞僩丄慡壒偼俀侽侽僙儞僩僆僋僞乕僽偼 侾俀侽侽僙儞僩偱昞偝傟傞丅恖娫偺壜挳幆暿尷奅乮曎暿鑷乯偼丄晀姶側恖偱丄俀僙儞僩丄楢懕揑敪壒偺忬懺偱俆僙儞僩偱偁傞偐傜丄偙偺揰偐傜傕扨埵偲偟偰揔摉側戝偒偝帩偭偰偄傞丅 偙偺僙儞僩偵傛傞壒掱昞帵朄偼丄懡偔偺挿強傪傕偭偰偄傞丅 乮侾乯捈姶揑偱傢偐傝傗偡偄丅 壒掱斾乮怳摦悢斾乯偵傛傞曽朄偼暘悢偺抣偺戝偒偝傪偨偑偄偵斾妑偟側偗傟偽側傜側偄偑丄僙儞僩偵傛傟偽捈偪偵僙儞僩悢偐傜壒掱偺戝偒偝 傪尒偄偩偡偙偲偑偱偒傞丅偨偲偊偽壒掱斾偺曽朄偱偼弮惓棪偺挿俀搙偼俉丗俋丄暯嬒棪挿俀搙偼侾丗俀丂12併俀偱昞偝傟傞偑丄僙儞僩偱帵偣 偽慜幰偼丄俀侽係僙儞僩丄屻幰偼俀侽侽僙儞僩偲側傝丄弮惓棪偺挿俀搙偺傎偆偑傢偢偐偵戝偒偄偙偲偑捈偪偵棟夝偱偒傞丅 傑偨丄敿壒傪扨埵偺婎弨偲偟偰偄傞偺偱丄壒奒偲枾愙側娭楢傪傕偪丄懠偺扨埵乮儈儕僆僋僞乕僽丄僒僽傽乕儖側偳乯偵斾傋偙偺揰偑偼傞偐偵 曋棙偱偁傞丅 乮俀乯壒掱偺嵎傗榓偑娙扨偵媮傔傜傟傞丅 壒掱斾乮怳摦悢斾乯偵傛傞応崌偼丄愊傗彜偵傛傞偐丄傑偨懳悢偺榓偐嵎傪媮傔側偗傟偽側傜側偄偑僙儞僩偱偼扨偵僙儞僩悢偺壛尭傪峴偊偽傛偄丅 僙儞僩偼丄怳摦斾偺12併俀傪掙偲偡傞懳悢抣偺侾侽侽攞丄傑偨偼俀傪掙偲偡傞懳悢抣偺侾俀侽侽攞偱昞偝傟傞丅 偡側傢偪斾俬偺僙儞僩悢偼丄 侾俀侽侽丂倢倧倗2丂俬丂亖倝僙儞僩 忢梡懳悢昞傪巊梡偡傞応崌偵偼 侾俀侽侽丂倢倧倗丂俬丂乛倢倧倗2丂亖丂倝僙儞僩 偲側傞丅 丂偙傟傜偺寢壥丄壒掱偺懳悢揑昞帵朄偱偁傞儈儕僆僋僞乕僽偲偼丄侾兪亖俇乛俆僙儞僩偺娭學偵側傝丄忢梡懳悢抣偵婎偯偔僒償傽乕儖偲偼丄 忋偺偹幃偐傜丄侾僒償傽乕儖亖係僙儞僩偺娭學偑惉傝棫偮丅 丂懳悢傪梡偄側偄惓悢榑揑側嵟傕娙扨側嶼弌朄偼師偺捠傝丅 壒掱斾傪帵偡俀悢偺偆偪戝偒偄悢偺俁攞偑彫偝偄悢偺係攞傛傝傕戝偒偔側偄側傜偽丄壒掱斾偺俀悢偺嵎偵俁係俈俈傪偐偗丄偦偺愊偺 彫悢揰埲壓傪柍帇偟偰壒掱斾偺俀忔偺榓偱妱傞丅偦偺彜偑係俆侽傛傝戝偒偄側傜偽丄偦傟偵侾傪壛偊傞丅偙傟偑壒掱偺僙儞僩悢偵側傞丅傕偟 壒掱斾偑係丗俁傛傝戝偒偔俁丗俀傛傝彫偝偄側傜偽丄戝偒偄悢偵俁傪丄彫偝偄悢偵係傪偐偗偰摼傜傟偨斾偵慜弎偺憖嶌傪壛偊丄嵟屻偵係俋俉 傪壛偊偰僙儞僩悢傪摼傞丅斾偑俁丗俀傛傝戝偒偄偲偒偼丄戝偒偄悢偵俀丄彫偝偄悢偵俁傪偐偗偰摼傜傟偨斾偵丄椺偺憖嶌傪壛偊丄嵟屻偺寢壥 偵俈侽俀傪壛偊傞偲傛偄丅 僙儞僩偺庬乆偺嶼弌朄偵偮偄偰偼丄僄儕僗偺亙彅柉懓偺壒奒俷値丂倲倛倕丂俵倳倱倝們倎倢丂俽們倎倢倕倱丂倧倖丂倁倎倰倝倧倳倱丂俶倎倲倝倧値倱亜乮侾俉俉俆乯丄 僿儖儉儂儖僣亙壒姶妎榑俿倧値倕倣倫倖倝値倓倳値倗倕値亜偺僄儕僗偵傛傞塸栿斉晅榐乮侾俉俈俆乯側偳偵徻弎偝 傟偰偄傞丅 ------------------------------------------------------------ |