切り札のフィットする確率　
　© boco_san (ぼこさん 2004/09 〜)　　　　　　　　メイリオ印刷
  1. はじめに
  2. 切り札のフィットする確率 ( 1 スーター ) ---- 確率の表 (1)
  3. 切り札のフィットする確率 ( 2 スーター ) ---- 確率の表 (2)
  4. 切り札のフィットする確率 ( ハンド･パターンごと )
    　　　　　Rule of 20 の意味 ---- 確率の表 (3)
  5. 切り札の枚数と発生確率 ----- 確率の表 (4)
  6. 切り札の偏りかたの相関 ----- 確率の表 (5)
    　　――― 付 録 ―――
  7. 確率の計算方法 [表 (1)]
  8. 確率の計算方法 [表 (2)]
  9. 確率の計算方法 [表 (3)]
  10. 確率の計算方法 [表 (4), (5)]
  11. 2 項係数の和公式の証明
はじめに

　 ブリッジでは，確率の数値を大まかに把握していることが必要です。
　 ブリッジの本によく載っているのは，たとえば，
　　　「 7 枚のスートが，ディフェンス側の二人に どのように分かれるか」
という確率です。これは，ディクレアラーがプレイする上で必要な確率です。

　 ところが，そのほかに，ビッドの過程でも確率について大まかに理解している必要があります。 これについては，まとまった確率の表を見かけることが全く無いので，自分で計算しました。
　 計算式などは，すべて後の方にまとめます。

切り札のフィットする確率 ( 1 スーター )

　 最初に取り上げるのは，たとえば，

「自分が 6 枚のスートを持っているときに，
　　　　　　　　パートナーが 2 枚以上持っている確率は ? 」
とか
「自分が 5 枚のスートを持っているときに，
　　　　　　　　パートナーが 3 枚以上持っている確率は ? 」
というような問題です。

その結果を 表 (1) に示します。
計算式に関心のある方は，後の方をお読み下さい。

《 確率の表 (1) 》
同一スートでの 自分の枚数とパートナーの枚数の相関 [ 数値は 発生確率(%) ]
自分の
枚数 		  8 枚
以上のフィット
確率 		パートナーの枚数
012345678910111213
0   1.2  0.1  1.5  7.418.727.524.813.9  4.9  1.0  0.1  0.0  0.0  0.0  0.0
1   3.4  0.2  2.610.622.928.621.610.1  2.9  0.5  0.0  0.0  0.0  0.0
2   8.5  0.5  4.114.526.728.117.7  6.7  1.5  0.2  0.0  0.0  0.0
3 18.1  0.8  6.419.229.625.913.3  4.0  0.7  0.1  0.0  0.0
4 33.7  1.5  9.624.231.122.2  9.1  2.1  0.3  0.0  0.0
5 54.4  2.513.929.230.617.4  5.4  0.9  0.1  0.0
6 76.3  4.319.533.427.812.1  2.7  0.3  0.0
7 92.9  7.126.235.722.8  7.1  1.0  0.1
8 10011.433.835.216.1  3.2  0.2
9 10018.241.130.8  9.0  0.9
10 10028.446.222.2  3.1
11 10043.945.610.5
12 10066.733.3
13 100100
　 この表の見方を説明しましょう。
　 あなたが，たとえば を 6 枚持っているとします。
　 このとき，パートナーが を持っている確率は
　　2 枚の場合が 33.4 %，3 枚の場合が 27.8 %，4 枚の場合が 12.1 %，…
　 それで，合計 8 枚ならフィットがあると考えて，これらの数値を合計すると，
ハートで フィットのある確率が 76.3 % となります。

　 この確率 76.3 % がかなり高いので，6 枚の良いスートがあったら，パートナーに 2 枚以上を 期待してプリエンプトしてよい … と言えます。
　 分かりやすく言うと，自分で 6 枚持っていれば，4 回のうち 3 回は，合計 8 枚以上のフィットがあります。

　また，自分が 5 枚持っているとき，パートナーが 3 枚以上で サポートしてくれる確率は， 54.4 % であることが分かります。 1 や 1 オープンしたときの経験と合っているでしょうか…。

切り札のフィットする確率 ( 2 スーター )

　 次は，2 スーターの場合です。たとえば，

「自分が 5 枚と 4 枚を持っているときに， パートナーが
　 3 枚以上 または 4 枚以上を持っている確率は ? 」
というような問題です。
　 この結果を 表 (2) に示します。
《 確率の表 (2)　2 スーターの枚数とフィット確率(%) 》
自分が持っている 2 スーターの枚数
枚数334454556566
 8 枚以上のフィット確率35.260.374.283.592.296.4

　 いくつか説明を加えておきましょう。

切り札のフィットする確率 (ハンド･パターンごと)

　 確率の計算をらくにできるようになったので，今度は，ハンド･パターンごとにフィット確率を計算してみました。

　 ここでは，とくに，4-3-3-3 のバランス･ハンドに注目します。経験からよく知られていることですが， 4-3-3-3 の形は 何をするにも不利です。
　 スートのコントラクトでは，切り札のフィットが見つかりくいし，仮に見つかっても， 自分の手では切ることができません。そうかと言って，ノートランプでは，長い (マイナー ) スートで 走ることもできません。結局， 4-3-3-3 の場合には，高い HCP を持っていないと勝負になりません。 そのため，4-3-3-3 の形では 12 HCP ではオープンしないのが普通です。
　 こういう 4-3-3-3 型ハンドの不利な状況を，フィット確率という数値により定量することが目的です。
　 確率の計算結果は，次のようになりました。

《 確率の表 (3) 》
ハンド
パターン		フィットする確率(%) Rule of 20
でのカウント 		発生確率
(%)
 8 枚以上 9 枚以上
 4 ‐3 ‐3 ‐3 76.425.6 710.54
 4 ‐4 ‐3 ‐2 79.129.0 821.55
 4 ‐4 ‐4 ‐1 83.134.0 8 2.99
 5 ‐3 ‐3 ‐2 82.534.5 815.52
 5 ‐4 ‐2 ‐2 84.537.5 910.58
 5 ‐4 ‐3 ‐1 85.839.2 912.93
 5 ‐4 ‐4 ‐0 89.344.4 9 1.24
 5 ‐5 ‐2 ‐1 89.546.710 3.17
 5 ‐5 ‐3 ‐0 91.048.910 0.90
 6 ‐3 ‐2 ‐2 90.249.8 9 5.64
 6 ‐3 ‐3 ‐1 91.051.2 9 3.45
 6 ‐4 ‐2 ‐1 92.153.610 4.70

　 4-3-3-3 と 4-4-3-2 の 2 つの場合には，フィット確率が低く，とくに 4-3-3-3 では 際立って確率が低くなっています。このように，4-3-3-3 が損な形であることは，フィット確率の低さからも 裏付けられました。

　右から 2 番目の欄に示したのは，2 スートの合計枚数です。
　この結果から，ルールオブ 20 によるカウントとフィット確率とが良い比例関係 (１次式の関係 ) にあることが分かります

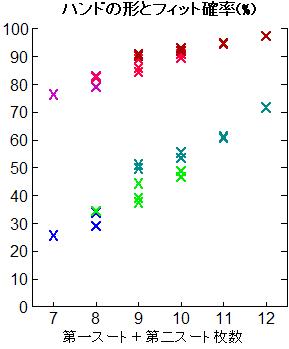graph 　 数字だけでは分かりにくいので，これを，右のように，グラフにしました。
　 縦軸はフィット確率を示しており，X は 8 枚フィット， X は 9 枚フィットの確率です。
　 第１スートの枚数 (4, 5, 6) により，どちらも三色に 色分けしています。
横軸には，上位 2 スートの合計枚数を取りました。 このグラフから，フィット確率と Rule of 20 のカウントが， 非常に強い相関を持つことが分かります。
　 オープニング･ビッドの段階では自分のカードしか見えていないので，自分の手がパートナーの手と どのくらいよくフィットするかは全く分からないのですが，Rule of 20 に従えば，フィット確率の 高いハンドをオープンしやすいと言えます。

　 Rule of 20 について，私がこれまで漠然と理解していたのは ( 正確に言うと， 理解していると思っていたのは )，
　 Rule of 20 を使えば，
　 「もしもパートナーと切り札のフィットがあれば，短いスートで切れるとか，長いスートで走れるから有利」
　 と いうことでした。しかし,「もしも」と言うのは，間違いだったのです。
　 Rule of 20 を使えば，

「HCP がいくらか不足でも，パートナーとフィットする確率がそもそも高いので，短いスートで切れるとか，長いスートで走れるから有利」
というのが，正しい理解なのです。

要するに，HCP (手の強さ ) とは無関係に，切り札のフィット確率は

第 1 スートの枚数　＋　第 2 スートの枚数
と，かなり強い 1 次関係にあります (上図)。
　 この関係に，手の強さ(HCP)を加味したのが，Rule of 20 です。

　 なお，本稿を 2004 年に公表したとき,「表 (3) およびグラフで [4333] ハンドのフィット確率が低すぎるように思う」との ご指摘を nagunatu さんから頂き，数値計算のミスを発見して 訂正いたしました。 ここに記して お礼申し上げます｡

切り札の枚数と発生確率

　 こんどは，たとえば，
　　　　　「N-S ペアが合計して 10 枚の切り札を持つ確率はいくらか ? 」
というような問題です。その結果は 次の通りです。

《 確率の表 (4) 》
枚数 7 8 9 10 11 12 13
確率(%)  15.7   45.7   28.1    8.7    1.6    0.16    0.01 

　 この表から，合計 8 枚の場合が最も多い(45.7%) ことが 分かります。 次に多いのが 9 枚で， この 2 つで 73.9 % を占めます。
　 10 枚の切り札は，約 11 回に 1 回の割合で発生します。

切り札の偏りかたの相関

　 最後に計算するのは，N-S ペアの切り札枚数と，E-W ペアの切り札枚数の間の相関です。 たとえば，

「味方が合計 10 枚の切り札を持っているとき， 相手方も合計 10 枚の切り札を持つ確率はいくらか? 」
というような問題です。計算の詳細は付録に回して，結果は次のようになりました。
« 確率の表 (5) »
切り札枚数の相関 (発生確率 %)
 味方の
枚数 		相手方の枚数
78910111213発生確率
766.6733.33*****15.74%
811.4758.8625.08  4.30  0.29**45.74%
9*40.8341.6414.58  2.71 0.23 0.0128.10%
10*22.6847.2523.43  5.85 0.75 0.04  8.67%
11*  8.4848.1632.10  9.67 1.49 0.09  1.58%
12**41.0041.1714.94 2.69 0.19  0.16%
13**24.3048.6022.08 4.64 0.38  0.01%

　 表の中の星印 (*) は，確率が 0 であることを示します。つまり，そういうことは，絶対に起こりません。
　 この表は，Cohen の 2 冊目の本に載っているもの (Edward Schwan による 1000 個のディールでの コンピュータ･シミュレーション) に対応します。
ただし，上の表は 数学的に厳密なものであり，シミュレーションではありません｡

　 この表から，いくつかのことが分かります。
　 (1) 味方が 7 枚の切り札を持つとき，相手方の切り札は，7 枚 または 8 枚のどちらかであって, 9 枚以上ではありません。そして，7 枚の場合が 8 枚の 2 倍頻繁に発生します。
　 (2) 全体を通じて最も発生しやすいのは 双方とも 8 枚持つ場合です｡
その発生確率は，45.74% × 58.86% = 26.98% (ほぼ，4 回に 1 回) です｡
　 したがって，競り合いは  2 の代で起こりやすいことが分かります｡
　 (3) 味方が切り札を 9 枚持つ場合には，相手方の切り札は 8 枚，9 枚の場合が ほぼ等しい確率 40% で起こります。このような知識は，LoTT に基づく判断を行う上で 役に立ちます。
　 (4) 味方の切り札が 10 枚のときには，相手方の切り札は 8〜10 枚に分布して 判断に困ります。

　 その判断を助けるには，この表を更に詳しくして，ダブル･フィットまで 調べる必要があります。そこまで詳しく調べた結果が，下の表です。

« Probability Table (5a) » (Updated)
Correlation between Trump Distributions
[8d] = 8 + 8;　　[9d] = 9 + 8 as well as 9 + 9.
 Our Trumps Their Trumps
7 88d 99d10111213Frequency
766.6733.33*******15.74%
814.8166.67*18.52*****35.41%
8d**32.1147.57*19.03  1.30**10.34%
9*32.4324.3236.04*  7.21***20.22%
9d****55.9933.50  9.66 0.82 0.02  7.88%
10**22.6816.8030.4523.43  5.85 0.75 0.04  8.67%
11**  8.48*48.1632.10  9.67 1.49 0.09  1.58%
12****41.0041.1714.94 2.69 0.19  0.16%
13****24.3048.6022.08 4.64 0.38  0.01%
(これを更に詳しく調べた表も見られます)

変更したのは，次の 2 つの分類です。
　 ◇ 8 枚フィットを，単純 8 枚フィット [8] と ダブルフィット [8d] (8 枚 + 8 枚) に 細分しました。
　 ◇ 同様に，9 枚フィットを 単純 9 枚フィット [9] と ダブルフィット [9d] に細分しました。 ここで [9d] は，9 + 8 枚 および 9 + 9 枚の両方を含みます。

　全体として，こちらがよくフィットしていれば 相手もよくフィットしています｡ つまり，カードの 強さの分布 は 場合によって まちまちですが，カードの枚数の分布は， かなり公平です。

　この表を見ると，いくつかの面白いことに気づきます。

　o まず気づくのは，[8] と [8d] の交点の確率が 0 であること ―― すなわち，片方だけが 8 枚のダブルフィットが 持つことは，あり得ません。こちらに [8d] があれば，相手方には 少なくとも [8d] (32%) があります (単純な 8 枚フィット [8] はありえない) 。[8d] でなければ，[9] (46%) または [10] (19%) があります。
　 o 10 枚フィット [10] が片方にある場合も同様です。 このとき，相手方には，少なくとも [8d] があります。単純８枚フィットはあり得ません。
　 o これに対して，こちらに 9 枚の単純フィット [9] がある場合には， 相手方の切り札の発生確率は [8], [8d], [9] にほぼ等しく分布するので，ここから競り合いビッドに関して有効な情報を得ることはできません。
　 o ただし，[9d] になると，事情は一変します。 このとき，相手方は少なくとも [9d] を持ちます。 [8] も [8d] もあり得ません。

　 以上のようなことがあるので，味方に [8d], [9d], [10] のフィットがある場合には，(合計トリック数が大きいことが事前に分かるので) 相手方がビッドする前に先行して プリエンプトする有効性が保証されます。つまり，上のような確率の知識と LoTT とを組み合わせると，状況に応じた競り合いが可能になります。
　確率の知識無しに 単に LoTT だけでは，理解できないことです。

補足説明
　 上の表を眺めて，星印 [*] の欄の確率がなぜ 0 なのか疑問を感じる読者のために， 説明を補足します。 確率の計算は，付録のようにして 行いますが，その結果が 0 になる場合というのは，計算しなくても，その理由を 説明できます。
　 ここでは，[9] と [9d] を例として，なぜこの 2 つで上のような大きな違いが生じるかを 考えましょう。
　 味方に 単純 9 枚フィット [9] がある場合，味方 2 人の 26 枚のカードを 4 スートに分けて ( 9, a, b, c ) と します。 2 人のカードは，合計 26 枚ですから
　　　　　　　　　a + b + c = 26 − 9 = 17
です。
今は，単純 9 枚フィットを考えているので，
　　　　　　　　　7 ≧ a ≧ b ≧ c
(9,a,b,c ) ( 4, x, y, z )
(9,7,7,3)(4,6,6,10) = [10]
(9,7,6,4)(4,6,7,9) = [9]
(9,7,5,5)(4,6,8,8) = [8d]
(9,6,6,5)(4,7,7,8) = [8]
が成り立ちます ( 8 以上だとダブルフィットになってしまう)。この 2 つの条件を満たす数の組は, 4 通りあります (右表)。
　 他方，相手方 2 人の持ち札を考えると，
第 1 スートの枚数は，13 − 9 = 4 です。
その他 3 スートの枚数 x, y, z は， これら 4 通りに対応して (その裏返しとして) 13 からの補数を取って
　　　　　 x = 13 − a,　 y = 13 − b,　 z = 13 − c
により決まります。
　 このようにして，味方が単純 9 枚フィットの場合，相手方のフィットは [10], [9], [8d], [8] の どれかに限ることが分かります。
　 9 枚ダブルフィット [9d] の場合も同様に考えます。ただし，この場合には，味方のフィットとして 9+8，9+9 の 2 通り を調べる必要があります。
ここでは，9+8 の場合を調べましょう。
　 味方 2 人の持ち札 26 枚を 4 スートに分けて ( 9, 8, b, c ) とすると
　　　　　　　　　b + c = 26 − ( 9 + 8 ) = 9
です。
( 9, 8, b, c ) ( 4, 5, y, z )
(9,8,7,2)(4,5,6,11) = [11]
(9,8,6,3)(4,5,7,10) = [10]
(9,8,5,4)(4,5,8,9) = [9d]

　 ここで，b と c は (表を短くするために, 3 重フィットの場合を除くと)，
　　　　　　　7 ≧ b ≧ c
を満たします。相手方の持ち札は，上と同じく 13 からの補数を取って得られるので，結局， 右の 3 通りが得られます。
　 したがって，味方が [9d] の場合には，相手方は [9d], [10], [11] の どれかを持ちます。

確率の計算方法 [表 (1)]

　 確率の計算は，結果の数値を知れば十分という方が大部分でしょう。
でも，どうやってそれを計算したかを 書いておかないと，その数値が正しいという保証がありません。そこで， 2 項係数 nCr = n ! / r ! (n−r)! を 使った計算方法を ここに書き留めておきます。

　 表 (1) では，たとえば，

「 4 人のプレイヤー  N, E, S, W  のうち，N  が を 6 枚持っているとき
　そのパートナー  S  が を 2 枚持つ確率はいくらか ? 」
を訊ねます。
　 そこで，これを一般化して
「プレイヤー  N  が を a 枚持っているときに，
　そのパートナー  S  が を x 枚持つ確率 P (a, x ) を求めよ 」
という問題を考えます。
その答は，以下に説明するように
P (a, x )  =   13Cx   26C13−a-x  / 39C13−a
となります。

　 スペードの枚数に注目して考えると，

  1. N が持つ 13 枚のうち， が a 枚，その他のスートが 13 - a 枚なので，
    この組み合わせは 13Ca 通りあります。
  2. S が持つ 13 枚のうち， が x 枚，その他のスートが 13 - x 枚なので，
    この組み合わせは 13Cx 通りあります。
  3. E と W が持つ 26 枚のうち， が 13-a-x 枚，その他のスートが 13+a+x 枚なので， この組み合わせは 26C13−a−x 通りあります。
以上を掛けると，場合の数が
　　　　　N (a, x )　= 13Ca × 13Cx × 26C13−a−x
となります。これを x について加えた総数
  Σx N (a, x )  ＝ 13Ca　×　Σx　13Cx × 26C13−a−x ＝ 13Ca × 39C13−a
で割ることにより，上の確率が得られます。
　 なお，総和の計算では， 2 項係数の和公式
Σx　nCx × mCp−x　＝　n+mCp
を使いました (岩波全書，数学公式 Ⅱ，p.13，第 5 行目の公式 ) 。
この公式の証明を，末尾に記載します。
確率の計算方法 [表(2)]

　 表 (2) では，たとえば，

「プレイヤー N が を 5 枚と を 4 枚持っているとき，
　パートナー S が を 3 枚以上 または を 4 枚以上持つ確率は
　 いくらか ? 」
を訊ねます。
　 そこで，これを一般化して
「プレイヤー N が を a 枚， を b 枚持っているとき
　パートナー S が を x 枚， を y 枚持つ確率 P (x, y ) を求めよ」
という問題を考えます。
　 その答は，以下に説明するように
P (x, y )  =   13−aCx   13−bCy   13+a+bC13−x−y   / 39C13
となります。そして，この確率 P (x, y )  を
　a + x ≧ 8  or  b + y ≧ 8　( の少なくともどちらかの合計枚数が 8 以上)
を満たす場合について加えると，表 (2) の結果が得られます。
  1. スペードの枚数に注目すると，
    合計 13 枚のうち，N が a 枚，S が x 枚，残りの 13-a-x 枚を E と W が持つので， この組み合わせは 13Ca × 13−aCx 通りあります。
  2. ハートの枚数に注目すると，
    合計 13 枚のうち，N が b 枚，S が y 枚，残りの 13-b-y 枚を E と W が持つので， この組み合わせは 13Cb × 13−bCy 通りあります。
  3. ダイヤモンドとクラブの 26 枚は，ひとまとめにして考えます。
    26 枚のうち，13-a-b 枚を N が持ち，残りの 13+a+b 枚を S, E, W の
    三人で分けます。そのうち，S は 13-x-y 枚 を 持つので，
    場合の数は，26C13−a−b × 13+a+bC13−x−y 通り あります。
以上を掛けると，場合の数が 　 N (x, y )　= 13Ca × 13−aCx × 13Cb × 13−bCy × 26C13−a−b × 13+a+bC13−x−y となります。ただし，ここでは a と b が定数なので，x と y を含む因子だけを
抜き出すと
　　　　　N (x, y )　= 13−aCx  × 13−bCy  × 13+a+bC13−x−y
これを，x と y について加えた総数
　　Σx   Σy   N (x, y )   ＝  Σx   Σy　 13−aCx  × 13−bCy  × 13+a+bC13−x−y
　　　　　　　　　　   ＝  Σx　 13−aCx  × 26+aC13−x
　　　　　　　　　　 　＝　39C13
で割ることにより，上の確率 P (x, y ) が得られます。

確率の計算方法 [表 (3)]

　 表 (3) では，たとえば，

「 プレイヤー N が を 4 枚， を 3 枚， を 3 枚， を 3 枚 持っているとき，
　パートナー S が を 4 枚以上
　　　　　　 または を 5 枚以上，
　　　　　　 または を 5 枚以上，
　　　　　　 または を 5 枚以上 持つ確率はいくらか ? 」
を訊ねます。
　 そこで，これを一般化して
「プレイヤー N が を a 枚， を b 枚， を c 枚， を 13-a-b-c 枚 持つとき，
　パートナー S が を x 枚， を y 枚， を z 枚， を 13-x-y-z 枚 持つ確率 P (x, y, z) を求めよ 」
という問題を考えます。
　その結果は，
P (x, y, z )  =   13−aCx   13−bCy   13−cCz   a+b+cC13−x−y−z   / 39C13
となります。そして，この確率 P (x, y, z )　を
　　　　　[どれかのスートの合計枚数が 8 以上 / 9 以上]
の場合について加えると，表(3) の結果が得られます。
  1. スペードの枚数に注目すると，
    合計 13 枚のうち，N が a 枚，S が x 枚，残りの 13-a-x 枚を E と W が
    持つので，この組み合わせは 13Ca × 13−aCx 通りあります。
  2. ハートの枚数に注目すると，
    合計 13 枚のうち，N が b 枚，S が y 枚，残りの 13-b-y 枚を E と W が持つので， この組み合わせは 13Cb × 13−bCy 通りあります。
  3. ダイヤモンドの枚数に注目すると，
    合計 13 枚のうち，N が c 枚，S が z 枚，残りの 13-c-z 枚を E と W が
    持つので， この組み合わせは 13Cc × 13−cCz 通りあります。
  4. 最後に，クラブに注目します。
    クラブ 13 枚のうち，13-a-b-c 枚を N が持ち，残りの a+b+c 枚を
    S, E, W の 3 人で分けます。
    この a+b+c 枚のうち，13-x-y-z 枚 を S が持つので，
    場合の数は，13C13−a−b−c × a+b+cC13−x−y−z 通り あります。
以上を掛けると，場合の数が
　N (x, y, z )   =   13Ca × 13−aCx  ×  13Cb × 13−bCy  ×  13Cc × 13−cCz
　　　　　　　　×　 13Ca+b+c × a+b+cC13−x−y−z
となります。ただし，ここでは a, b, c が定数なので，x, y, z を含む因子だけを抜き出すと
　　　N (x, y, z )   =   13−aCx  × 13−bCy  × 13−cCz  × a+b+cC13−x−y−z
これを x, y, z について加えた総数
　　　　　Σx Σy Σz 　N (x, y, z)  ＝ 39C13
で割ることにより，上の確率 P (x, y, z ) が得られます。

確率の計算方法 [表 (4),(5)]

　表(5) のような確率は，次のように考えて計算します。

　 52 枚のカードをどう配るかという問題ですが，いまは，個々のプレイヤーへの配り方は問題になっていません。 各ペアへのカードの分配だけが問題になっています。
　 したがって，

　　　　　「52 枚のカードを 2 組のペアに 26 枚ずつ配る」
と考えます。このときの配り方は，組み合わせの記号を使って，全部で 52C26 通りあります。この 52C26 通りの 分配法 (根元事象 ) がどれも同様に確からしいと仮定して，確率を計算します。
　 N-S に配られた 26 枚のカードの内訳が
　　　　 s 枚， h 枚， d 枚， c 枚
としましょう。 このとき，もちろん
　　　　　　s + h + d + c = 26
が成り立ちます。このような配り方は
　　　　　　13Cs × 13Ch × 13Cd × 13Cc
通りあります。
なぜなら，各スート毎に 13 枚のカードがこのように配られるからです。
《 多重度の表 》
パターン例多重度
３つ同じ [7775] 4
2 つ同じ対 [7766] 4! / 2! 2! = 6 
2 つ同じ[8864] 4! / 2! = 12 
すべて異なる[9863]4! = 24
　 実際には，これに右表のような 4 通りの多重度を掛けます。 たとえば，[7775] 型では，( s, h, d, c ) = 7775, 7757, 7577, 5777 の 4 通りがあります。
　 例として，N-S ペアの最も長いスートが 7 枚の場合を調べましょう。 すなわち，8 枚以上のフィットが無い場合です。
　 このような運の悪いディールは，次の 2 種類です。
　　(a)  7 ‐ 7 ‐ 6 ‐ 6
この分布は，
　　13C7 × 13C7 × 13C6 × 13C6
通りあります。実際には　(s, h, d, c ) = (7, 7, 6, 6) だけでなく (7, 6, 7, 6) などのように合計 6 通りがあるので， この多重度 6 を掛けると，場合の数が
　N (a)  =  6 × ( 13C7 × 13C7 × 13C6 × 13C6 )　＝　5202 59937 50016
となります。
　 この場合，E-W の持ち札は，7 ‐ 7 ‐ 6 ‐ 6 を裏返した 6 ‐ 6 ‐ 7 ‐ 7 となるので，双方とも 8 枚フィットがありません。

もうひとつの分布
　　(b)  7 ‐7 ‐7 ‐5
では，場合の数が

　　　　　　13C7 × 13C7 × 13C7 × 13C5
となりますが，実際には　(s, h, d, c) = (7, 7, 7, 5) だけでなく (7, 7, 5, 7) などのように 合計 4 通りがあるので， これを掛けて，
　　N (b)　=　4 × ( 13C7 × 13C7 × 13C7 × 13C5 )  ＝  2601 29968 75008
となります。
　 この場合，E-W の持ち札は，7 ‐ 7 ‐ 7 ‐ 5 を裏返した 6 ‐ 6 ‐ 6 ‐ 8 となるので， E-W だけに 8 枚フィットがあります。
　 この 2 つの場合 (a) と (b) の比をとると，13C6 = 13C7 であることに注意して， その結果は
　　　　　N (a) ： N (b) = 　6 × 13C6 ： 4 × 13C5 = 2 ： 1
です。上の 2 つの数字の比が正確に 2 倍になっていることからも，これは分かります。
　 さらに，上の N (a) と N (b) を加えて，その結果を 全体の場合の数
　　　　　　52C26　＝　49591 85320 48104
で割ると，7 枚フィットの発生確率 15.736254% が得られます。

　 以上のようにして，すべての場合の確率を (Visual Basic でプログラムを作成して ) 計算しました。したがって，上の表(1)〜(5) の確率は，シミュレーションに よるものではなく，すべて厳密な数値です。

　 ブリッジで確率を計算するときの考え方は，Durango Bill さんの ウェブサイト に説明されています。

2 項係数の和公式の証明

　 上で何度も用いた 2 項係数の和公式は，次のようにして証明できます。
　 出発点になるのは，よく知られた 2 項展開の公式
　　　　　Σx　nCx　Ax B n −x ＝ ( A + B )n
です。
　この公式が成り立つ理由は，この右辺を
( A + B ) n = (A+B) × (A+B) × … × (A+B)
と展開すると，右辺で A を  x 個，B を  n-x 個選ぶ組み合わせが nCx 回あるからです。
　ただし，以下では B = 1 とおいた簡単な場合
　　　　　Σx   nCx  Ax　＝　( A + 1 )n 　　　　　　　　　　　… [1]
だけを使います。
　ここで変数を  n → m，x → y と書き換えても同じ公式
　　　　　Σy　mCy  A y　＝　( A + 1 )m 　　　　　　　　　　… [2]
が成り立つので，この両辺を それぞれ掛け合わせると
　　　　　Σx Σy　nCx  mCy　Ax+y　＝　( A + 1 )m+n 　　　　… [3]
が得られます。ところが，[3] の右辺は 2 項展開 [1] により展開できます。
　　　　　　( A + 1 )m+n ＝ Σp　m+nCp  A p 　　　　　　 　　… [4]
この両辺の A p の係数を等しいとおいて ( [3] の左辺から y = p - x の項だけを抜き出せば ) ， 求める和公式
　　　　　Σx　nCx　mCp−x　＝　n+mCp
が得られます。