Larry and the Law
by Larry Cohen

---

　1.  切り札の枚数を数える.
　2.  法則を適用しない場合.
　3.  法則による競り合いの指針を適用する.

---

　ブリッジを始める人は 誰しも，A=4, K=3, Q=2, J=1 として，合計の HCP を数える。そして パートナーと合計 何点持っているかに基づいて ビッドを進める。合計 25〜26 HCP あれば，ゲームに行こうとするし，33 HCP もあれば スラムを狙おうとする。
　オークションが競り合いの場合には，これと同様に，パートナーと合計 何枚の切り札を持っているかに基づいてビッドを進める。これが有効な理由は，法則から 次の単純な指針が導かれるからである： 　自分が持っている切り札の枚数は もちろん ハッキリしているが，パートナーの切り札の枚数は，どうやって分かるのだろうか？ 多くの場合，パートナーのビッドが その手がかりを与えてくれる。たとえば，パートナーが ウィーク２で 2 オープンした場合，パートナーは 良い６枚スートを持っていると想像できる。この６枚に 自分が持っている枚数を加えて，２人の合計枚数が得られる。
　法則を応用する場合には，これが ウィーク２に どう応えるかの出発点になる。

　法則を必要とするのは，競り合いの場合に限られる。もしも 味方が 圧倒的に強ければ，相手方が オークションに参入することは無く，その場合には，法則とその教えるところを無視する。
　たとえば，このハンドは，法則と全く関係が無い。見れば分かるように，[この手では５トリックを確実に取れそうなので]，パートナーの手と合わせて，合計 10 トリックを取れると想像できる。
　４人の手は，たとえば，このようになっているだろう。 　ディクレアラーのハートの ルーザー２枚は，ダミーでラフするか，あるいは，ダミーのダイヤモンドをエスタブリッシュして その下に捨てることができる。
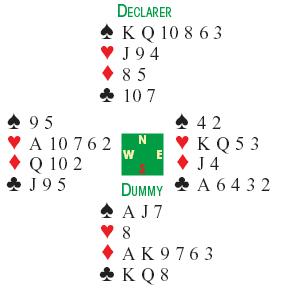
こうして，4 は メークすると期待できる。この場合，切り札の枚数は無関係である。4 をメークしたいと思うので，4 をビッドする。
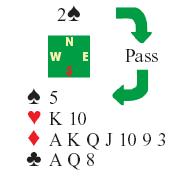
これと同じ考え方で説明できる例を もう１つ挙げよう｡ ここでは 3NT ができそうなので, 3NT をビッドしたい｡ ダイヤモンド７トリックとクラブ１トリックを 確実に取れる。残りの１トリックは, Q, K, あるいは パートナーの スペードで取れるであろう。
　要するに，ゲームが確実にあると考えられる場合には 素直にゲームをビッドする。このとき，法則については何も考えない。
　パートナーが ウィーク２でオープンして，自分が 法則を無視するもう１つの状況は，ゲームへの誘いを掛けられる程度の強さを 自分が持っている場合である。
この場合，もしも パートナーの 2 オープンが 良い手ならば，ゲームがあるし，さもなければ，ゲームは無い。
　だが，ここで 3 を応えるのは，後述のように，誘いではない。したがって，パートナーに その状況を伝えてくれるよう要求するビッドが 何か必要である。そのために使われるのが，フォーシング 2NT コンベンションである。
　この 2NT にパートナーが 3 を返して 余分の強さを示さなければ，こちらは それをパスして，パートスコアに落ち着く。もしも パートナーが スペード以外のスートをビッドして 余分の強さを示せば，こちらは 4 に上がる。
　この例の場合，手元の切り札は３枚であるが，こちらは 最良のコントラクトを目指しており，相手方が割り込む様子が無いので，法則を適用することはしない。

　パートナーが ウィーク２ オープンして，自分の手の強さが不足しており，ゲームの見込みが無いと考えられる場合には，競り合いを考える。右オポがパスしている場合には，競り合いは未だ発生していないが，いずれは，競り合いになる。この場合には，法則の適用を考え始める。

　パートナーのビッドが ウィーク２の場合には，この適用は 非常にやさしい。ビッドすべきか否か，ビッドするとして どの代をビッドすべきか を決めるには，2人の手にある切り札の枚数を数えるだけでよい。
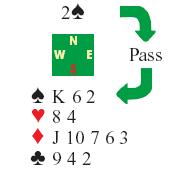
　このハンドの場合，自分からゲームに行こうとか，パートナーにゲームの誘いを掛けようとか，そんなことは考えない。それよりも，"法則による競り合いの方針" を適用して考える。自分は スペードを３枚持っている。パートナーの６枚と合わせて，切り札は 合計９枚ある。だから ９枚に相当する代まで競り合って，3 をビッドする。
　2 を１つ上げて 3 をビッドするのは，誘いではない。パートナーは，これをパスするものと期待されている。自分は この 3 をメークするつもりなのか？ 否，それは どうでもよい。3で負けることによる失点が，相手側が最良のコントラクトで得る得点を 下回ると考えて，このようにビッドしている。私の 3 は，彼らが最良のコントラクトに到達するのを 困難にすることを目的としている。
　上の例では，East がパスしたので，競り合いは未だ発生していないように見える｡ たしかに，未だ発生していない。だが，こちらの２人の手に強さが無く，East も またパスするような手ならば，West は 必ず オークションに参入してくる。こちらの 3 は，オークションが こうして競り合いになることを見越したビッドである。
　それでは，もしも East が テイクアウト･ダブルを掛けるとか，３の代でオーバーコールした場合には，どうすべきか。その場合にも，やはり 切り札の合計枚数に従って, 3 をビッドする。
　ただし，East がジャンプして 4 オーバーコールした場合には，パスする。切り札の合計枚数を越えてまで 競り合うことはしない。
　もう少し強い手で 3 に上げることもある。右のハンドでは，ゲームに行くだけの強さは無い。したがって，法則を適用する :「切り札が合計９枚なので，3 をビッド」 右オポがパスしても 何かビッドしても 同じである。この 3 をメークしようというつもりは無い。
　このハンドの場合にも，ゲームは 到底 期待できない。切り札の枚数は 合計 6+4=10 枚ある。切り札 10 枚ならば，10 トリックに相当する代 すなわち 4 の代にジャンプして 4 をビッドする｡
　それでは，このように弱い手で 4，最初のハンドでも 4 ということになるが，パートナーは，いったい どうやってこの区別をつけるのだろうか？ パートナーがそれを知るのは，ダミーの手が開いた時だ！ (私のビッド 4 に パートナーは関わっていない)。それまでは，パートナーも相手方も みな 私が 何をしようとしているのか推測するしかありません。
　それでは，右のように，切り札のサポートが２枚以下の場合には どうなるのか？ ゲームの見込みが無ければ，パスする。切り札の枚数が 合計８枚以下の場合には，２の代，すなわち８トリックを越えて 競り合うことは しない。