How often you get Trump Fit with your partner
- Introduction
- Probability of Trump Fit ( 1 suiter hands) ---- Table (1)
- Probability of Trump Fit ( 2 suiter hands) ---- Table (2)
- Probability of Trump Fit (for all hand patterns) ,
and what Rule of 20 means ---- Table (3), Figure1 - How often and how many trumps your side gets,
Table (4) - Correlation between the Trump Distributions,
Table (5), Double-Fit Rule.
−−−−−−−−− Appendix −−−−−−−−−− - Calculation of probability [Table (1)]
- Calculation of probability [Table (2)]
- Calculation of probability [Table (3)]
- Calculation of probability [Tables (4), (5)]
In bridge, it's important to be, at least roughly, aware of probabilities.
We often find, in bridge books or on web sites, tables of probability, for example, for
What I'm about to talk here is another kind of probability, which you have to be aware when you're bidding. Bridge is certainly a game of probability.
The problem of utmost importance in bridge bidding is how to find a possible fitting in a trump suit with partner. Knowledge of fitting probabilities will help you in this process. Since I've never seen this kind of probability tables on any books nor on web sites (except one), nor in WikiPedia, I calculated them for myself. The results are shown below in five tables and one figure, which I'll explain in turn.
Indeed, fitting probabilities tell us quite a lot, most of which have been left unknown. You'll encounter below novel concepts like Bergen count and Double-Fit Rule and their usefulness. Even the concept of fitting probabilities will sound novel, since they haven't been studied systematically.
Learned readers are invited to mathematical details expounded in four appendices.
The first question, we ask on fitting probabilities, is, for example,
Numerical result obtained from that mathematical formula is shown in Table (1) below. Please notice that this table (as well as the ones to follow) is not a result of any computer simulations. It gives mathematically exact values of the probabilities.
| Your cards | Fit proba -bility | Number of partner's cards in the same suit | |||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | ||
| 0 | 1.2 | 0.1 | 1.5 | 7.4 | 18.7 | 27.5 | 24.8 | 13.9 | 4.9 | 1.0 | 0.1 | 0.0 | 0.0 | 0.0 | 0.0 |
| 1 | 3.4 | 0.2 | 2.6 | 10.6 | 22.9 | 28.6 | 21.6 | 10.1 | 2.9 | 0.5 | 0.0 | 0.0 | 0.0 | 0.0 | |
| 2 | 8.5 | 0.5 | 4.1 | 14.5 | 26.7 | 28.1 | 17.7 | 6.7 | 1.5 | 0.2 | 0.0 | 0.0 | 0.0 | ||
| 3 | 18.1 | 0.8 | 6.4 | 19.2 | 29.6 | 25.9 | 13.3 | 4.0 | 0.7 | 0.1 | 0.0 | 0.0 | |||
| 4 | 33.7 | 1.5 | 9.6 | 24.2 | 31.1 | 22.2 | 9.1 | 2.1 | 0.3 | 0.0 | 0.0 | ||||
| 5 | 54.4 | 2.5 | 13.9 | 29.2 | 30.6 | 17.4 | 5.4 | 0.9 | 0.1 | 0.0 | |||||
| 6 | 76.3 | 4.3 | 19.5 | 33.4 | 27.8 | 12.1 | 2.7 | 0.3 | 0.0 | ||||||
| 7 | 92.9 | 7.1 | 26.2 | 35.7 | 22.8 | 7.1 | 1.0 | 0.1 | |||||||
| 8 | 100 | 11.4 | 33.8 | 35.2 | 16.1 | 3.2 | 0.2 | ||||||||
| 9 | 100 | 18.2 | 41.1 | 30.8 | 9.0 | 0.9 | |||||||||
| 10 | 100 | 28.4 | 46.2 | 22.2 | 3.1 | ||||||||||
| 11 | 100 | 43.9 | 45.6 | 10.5 | |||||||||||
| 12 | 100 | 66.7 | 33.3 | ||||||||||||
| 13 | 100 | 100 | |||||||||||||
Suppose you've 6 spades. Then, your partner will have
3 spades with probability 27.8 %,
4 spades with probability 12.1 %, and so on.
What does this mean ?
It means that you may expect 2 or more cards in partner's hand, with a high probability 76.3%. In other words, when you've 6 cards in some suit, your side will have a fit in that suit in 3 deals out of 4.
Suppose now that you've 5 cards in a major suit and open your hand with 1
 or
1
or
1 .
In this case, your partner will support your bid (with 3 cards or more) with
probability 54.4%, i.e., half times you open.
.
In this case, your partner will support your bid (with 3 cards or more) with
probability 54.4%, i.e., half times you open.
Did you know these probabilities ?
A second question occurs, when you have a 2-suiter hand,
Numerical result obtained is as follows:
| Your 2-suiter Hand | |||||||
| Your Holding | 3-3 | 4-3 | 4-4 | 5-3 | 5-4 | 5-5 | |
| Probability of 8-Card Fit or more (%) | 35.24 | 48.91 | 60.31 | 66.13 | 74.16 | 83.52 | |
We learn something from this table.
- The first member 3-3 in this table stands for the 3-3-4-3 balanced hand, which you'll open with 1NT, if you've an appropriate HCP. Partner will then support you (possibly through Jacoby transfer) with either of the major suits, having 5 cards. This happens almost once in three deals.
- In the second, 4-3 holding, the fitting probability remains as low as 33.7% (back to Table (1) and see the bold-face one), so long as you bid your first 4-card suit. However, there remains an additional possibility (ca.18%) that partner will have 5 cards in your second suit. So, in this holding, you'll find fitting about half times you open.
- In the third 4-4 case, if you (or partner) have a chance to bid your second suit, then the fitting probability almost doubles up from 33.7 to 60.3%. The result shows very clearly the need of bidding twice in this holding.
- The need becomes even more remarkable in 5-4 and 5-5 hands. So long as you bid your 5-card (first) suit, the fitting probability remains 54.4% (back again to Table (1)), which will jump up to 74.2 and 83.5%, respectively, when you can show your second suit. The result validates usefulness of Michaels cuebid and unusual NT overcall, which tells your 2-suiters with a single call.
| Distribution | Rule of 20 Requires | Fitting Probability |
5 3 3 x x x x
| 12 HCP | 54.4 % |
5 4 4 x x x x
| 11 HCP | 74.2 % |
 3 hand, you open with your 5-card suit.
Partner will have 3 cards in that suit with probability 54.4%. That is all for
the fitting probability, in this case.
3 hand, you open with your 5-card suit.
Partner will have 3 cards in that suit with probability 54.4%. That is all for
the fitting probability, in this case.
In 5
 4 hands, you can
show your 4-card suit on your second turn of bidding, which raises the fitting probability to 74.2%.
Marty Bergen duly appreciates this difference by reducing the requirement for HCP by 1 point.
4 hands, you can
show your 4-card suit on your second turn of bidding, which raises the fitting probability to 74.2%.
Marty Bergen duly appreciates this difference by reducing the requirement for HCP by 1 point.
| Distribution | Rule of 20 requires | Fitting Probability |
4 3 3 3 3 3 3
| 13 HCP | 33.7 % |
4 4 4 x x x x
| 12 HCP | 60.3 % |
 4 holding, which
almost doubles the fitting probability.
4 holding, which
almost doubles the fitting probability.
Did you know these probabilities ?
and What Rule of 20 means.
Having got acquainted with mathematics, I entered more complex situations (the result is simple, however). As many bridge players know well, the 4-3-3-3 card holding is worst, whatever you bid. Less bad is the most popular distribution 4-4-3-2. These two types occur almost once in 3 deals. On the other hand, everyone loves 5-5 holdings. The object here is to quantify (rather than qualify) this difference in the language of fitting probability. In other words, a third question we ask is,
| Hand Pattern | Fitting Probability(%) | Bergen Count | Frequency(%) | |
| 8 or more | 9 or more | |||
| 4-3-3-3 | 76.4 | 25.6 | 7 | 10.54 |
| 4-4-3-2 | 79.1 | 29.0 | 8 | 21.55 |
| 4-4-4-1 | 83.1 | 34.0 | 8 | 2.99 |
| 5-3-3-2 | 82.5 | 34.5 | 8 | 15.52 |
| 5-4-2-2 | 84.5 | 37.5 | 9 | 10.58 |
| 5-4-3-1 | 85.8 | 39.2 | 9 | 12.93 |
| 5-4-4-0 | 89.3 | 44.4 | 9 | 1.24 |
| 5-5-2-1 | 89.5 | 46.7 | 10 | 3.17 |
| 5-5-3-0 | 91.0 | 48.9 | 10 | 0.90 |
| 6-3-2-2 | 90.2 | 49.8 | 9 | 5.64 |
| 6-3-3-1 | 91.0 | 51.2 | 9 | 3.45 |
| 6-4-2-1 | 92.1 | 53.6 | 10 | 4.70 |
Bergen count in the table (so I call) obviously means
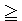 20
20
 The figure on the right clearly visualizes this correlation.
The abscissa gives the Bergen count, while the ordinate the fitting probability.
Crosses in red and wine are for 8-card fit (or more), while green and blue ones for 9-card fit (or more).
Overlapping crosses are colored somewhat differently.
I'll leave you this figure whatever for your interpreta-tion,
but mine is this:
The figure on the right clearly visualizes this correlation.
The abscissa gives the Bergen count, while the ordinate the fitting probability.
Crosses in red and wine are for 8-card fit (or more), while green and blue ones for 9-card fit (or more).
Overlapping crosses are colored somewhat differently.
I'll leave you this figure whatever for your interpreta-tion,
but mine is this:
During I'm bidding, I don't yet see partner's cards, and I'm quite uncertain if my cards will fit with partner's. However, if I obey the Rule of 20, even without knowledge of partner's hand, I'll more often open those hands that are more likely to fit with partner's hand.
At this point, I took notice that I had misunderstood the Rule of 20. The point may look trivial, but never. I had long believed, "the Rule is useful, because if I have a fit with partner, I would be able to utilize the long suit to draw, ruff, or run in NT, etc." Now, the above IF clause has turned out to be unnecessary. Every time I use the Rule to open, my hand is more likely to find fitting with partner's. That's what Marty Bergen's rule implies.
[NB] The above table downgrades the 4-4-3-2 hand against expectations. Surely, it works better than 4-3-3-3 in card-plays. Fitting probability doesn't consider such features.
A fourth question is quite simple. You may be concerned,
(to myself and my partner) ?
| Number of Cards | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Frequency(%) | 15.7 | 45.7 | 28.1 | 8.7 | 1.6 | 0.16 | 0.01 |
The fifth, final, problem is the correlation between the number of trumps held by the two sides. You may be concerned to ask, for example,
how often will they have 10 trumps in their hands ?
what would their hands be like at least ?
Is it a simple 8-card fit, or more ?
Motivated by Schwan's correlation table as well as by the double double-fit problem mentioned elsewhere, I attacked making it complete in the following two senses:
(1) I do not rely on computer simulations, but use mathe-matics (which is always exact).
(2) I do distinguish a simple 8-card fit from an 8-card double fit. Difference between simple and double fits is enormous, as many know. So, this distinction is essential.
Again, mathematics is given in Appendix, with the following result:
| Correlation between Trump Distributions | ||||||||||
| [8d] = 8 + 8; [9d] = 9 + 8 as well as 9 + 9. | ||||||||||
| Our Trumps | Their Trumps | |||||||||
| 7 | 8 | 8d | 9 | 9d | 10 | 11 | 12 | 13 | Frequency | |
| 7 | 66.67 | 33.33 | * | * | * | * | * | * | * | 15.74% |
| 8 | 14.81 | 66.67 | * | 18.52 | * | * | * | * | * | 35.41% |
| 8d | * | * | 32.11 | 47.57 | * | 19.03 | 1.30 | * | * | 10.34% |
| 9 | * | 32.43 | 24.32 | 36.04 | * | 7.21 | * | * | * | 20.22% |
| 9d | * | * | * | * | 55.99 | 33.50 | 9.66 | 0.82 | 0.02 | 7.88% |
| 10 | * | * | 22.68 | 16.80 | 30.45 | 23.43 | 5.85 | 0.75 | 0.04 | 8.67% |
| 11 | * | * | 8.48 | * | 48.16 | 32.10 | 9.67 | 1.49 | 0.09 | 1.58% |
| 12 | * | * | * | * | 41.00 | 41.17 | 14.94 | 2.69 | 0.19 | 0.16% |
| 13 | * | * | * | * | 24.30 | 48.60 | 22.08 | 4.64 | 0.38 | 0.01% |
Some comments are in order:
(b) 8d means an 8-card double fit [8+8], as distinguished from a simple 8-card fit, [8].
(c) Similarly, simple [9] is distinguished from 9d, which counts two kinds of double fit, [9+8] and [9+9].
(d) This table should be read row-wise. When summed in a row, total amounts to 100%. Column-wise reading is meaningless.
(e) A few words for readers who doubt about lack of symmet-ricity: If you multiply every row by its frequency on the right, and stop distinguishing double fits, then the table will restore symmet-ricity and validates Schwan's 1000 deal simulation.
- When you've 10 trumps in your two hands, as you asked above, opponents will have at least an 8-card double fit [8d]. They never will have a simple 8-card fit [8].
- The [8d] row tells us something so interesting, and I would put it as a Double-Fit Rule, which says,
Their hands can never be a simple 8-card fit [8].
The double-fit rule is explained plainly:
You have an 8-card double fit, holding 8
 8
8 a
a b in two hands.
Opponents will then hold its complementary 5
b in two hands.
Opponents will then hold its complementary 5 5
5 x
x y,
y,
where x + y = 26 − 5 − 5 = 16, because they have 26 cards in their hands. If x = 8, then y = 8, and if x = 9, then y = 7, etc. QED.
Most likely, many bridge players will have no interest in mathematics. Nevertheless, for the sake of completeness, I'll show below how I derived the mathematical expressions so that interested readers may confirm them and may even do computations by themselves.
You'll see everywhere below the symbol NCp , which stands for binomial coefficients in mathematics, or the number of combinations in statistics to choose p events (deals, in bridge) out of N events, NCp = N ! / p ! (N−p)! .
Calculation of probabilities starts with counting the number of events
(deals) of interest.
The rest is easy. Probability is obtained by dividing it by the
total number of events.
It is here naturally assumed that every event is evenly likely to happen.
Now, we call, for brevity, the 4 players N, E, S, and W.
In Table (1), we asked a problem like
how often does his partner S have 2 spades ?
find the probability P (a, x ) with which
his partner S has x cards in spades.
| 13Cx 26C13−a−x | ||
| P (a, x) | = | −−−−−−−−−−−−−−−−−−. |
| 39C13−a |
The proof goes as follows:
Just concentrate on the number of spade cards in the 4 players.
- Out of the 13 cards in his hand, N has a cards in spades, 13−a cards in the other suits. The number of such combinations is 13Ca .
- Out of the 13 cards in his hand, S has x cards in spades, 13−x cards in the other suits. The number of such combinations is 13Cx .
- Out of the 26 cards in their hands, E and W have 13−a−x cards in spades (remember that there are only 13 spades in the world), and 13+a+x cards in the other suits (because they have 26 in total). The number of such combinations is 26C13−a−x .
N (a, x) by its sum over x;
 x N (a, x) x N (a, x)
|
= 13Ca ×  x 13Cx × 26C13−a−x x 13Cx × 26C13−a−x
|
|
= 13Ca × 39C13−a |
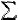 x nCx mCp−x
= n+mCp .
x nCx mCp−x
= n+mCp .
In the above calculation, the factor 13Ca cancels itself, since it does not depend on x. Note that a is a given constant, while x is a variable.
Table (1) gives the result based on this formula for P (a, x ).
In Table (2), we considered a problem like
how often will S have either 3 (or more) spades,
OR 4 (or more) hearts ?
S has x spades AND y hearts.
P (x, y ) = −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− .
39C13
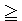 8 or b + y
8 or b + y 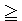 8
8
The proof goes as follows:
- First, concentrate on the spade cards.
Of the 13 cards, N takes a cards. From the remaining 13−a cards, S will take x cards, (and, E and W take the yet remaining 13−a−x cards). So, the number of combinations in the spade suit is 13Ca × 13−aCx . - Counting in the heart suit goes the same way, and will give the number of combinations 13Cb × 13−bCy .
- The 26 cards in diamonds and clubs will be counted in common.
Of those 26 cards, N will take 13−a−b cards (subtracting
his spades and hearts from 13).
Now, the 13+a+b cards (in diamonds and clubs) are left for S, E, and W, from which S takes 13−x−y (again subtracting). Distribution of the rest to E and W doesn't matter, and the number of combinations for diamonds and clubs is 26C13−a−b × 13+a+bC13−x−y .
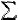 x x 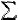 y
N (x, y) y
N (x, y)
|
= 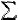 x x 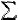 y
13−aCx
× 13−bCy
× 13+a+bC13−x−y y
13−aCx
× 13−bCy
× 13+a+bC13−x−y
|
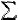 x
13−aCx
× 26+aC13−x x
13−aCx
× 26+aC13−x
| |
| = 39C13 , |
In Table (3), we asked,
P (x, y, z ) = −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−.
39C13
The problem looks hard and almost desperate (so did it to me, at first), but, not so, if you go step by step. Here we go.
- Start again with spade cards. Of the 13 spades, N takes a cards, S takes x cards, (remaining 13−a−x spade cards are held by E and W ). So, the number of combinations for such holdings is 13Ca × 13−aCx .
- Similarly, combinations in hearts are 13Cb × 13−bCy .
- And for diamonds, 13Cc × 13−cCz .
- Finally, consider clubs.
Of the 13 clubs, N takes 13−a−b−c cards (again, by subtraction), and the remaining a+b+c club cards are dealt among S, E, and W, from which S will take 13−x−y−z cards (here, also subtraction). So, in clubs, we have 13C13−a−b−c × a+b+cC13−x−y−z combinations in clubs.
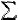 x
x 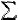 y
y 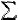 z
N (x, y, z) = 39C13 .
z
N (x, y, z) = 39C13 .
Now, let us attack the final problems.
In Tables (4) and (5), we're interested in how many trumps
each pair has in their two hands.
So, it doesn't matter how 26 cards are dealt within a pair.
Say, 5 and 4, or 6 and 3, or even 7 and 2, it doesn't matter. In any case, you've 9 trumps.
The problem is, therefore,
26 cards to each,
Now, suppose that N-S pair is dealt s spades, h hearts, d diamonds and c clubs. Their sum is, of course, equal to 26.
Let us consider in detail the case where N-S pair is dealt the least, seven, trumps. This occurs only in the following two types of distributions:
(a) 7 - 7 - 6 - 6.
In this case, E-W will have a complementary 6 - 6 - 7 - 7 distribution. So, both pairs have 7 trumps. This dealing will own
(b) 7 - 7 - 7 - 5,
E-W pair will have a complementary 6 - 6 - 6 - 8 distribution. So, they will have an 8-card fit. This dealing owns
Prob(b) = 5.2454 %.
On the basis of these mathematical formulas, I prepared computer programs in Visual Basic. Numerical results have been given in Tables (1) through (5).
 Durango Bill: presents mathematical
basis for probabilities in bridge.
Durango Bill: presents mathematical
basis for probabilities in bridge.
So long as the two works overlap, frequency in my Table (3) grees with his.
 Theo Groen: gives several
tables (calculated or simulated, as he says), which agree with my Table (1), frequency in Table (3), and Table (5), where he does not
distinguish single and double fits.
Theo Groen: gives several
tables (calculated or simulated, as he says), which agree with my Table (1), frequency in Table (3), and Table (5), where he does not
distinguish single and double fits.