ヒュベニの式を用いた、緯度・経度と距離・方位の相互変換の解説
2014/2/22 M,Yokota
コース角度計算ソフトを作成する過程で、高精度の緯度経度と距離の相互変換計算を調べたので、まとめたページを作成しました。
■PDF版はこちら
■エクセル関数を組み込んだサンプルエクセルファイルはこちらです。
地球の形状(回転楕円体)と緯度・経度
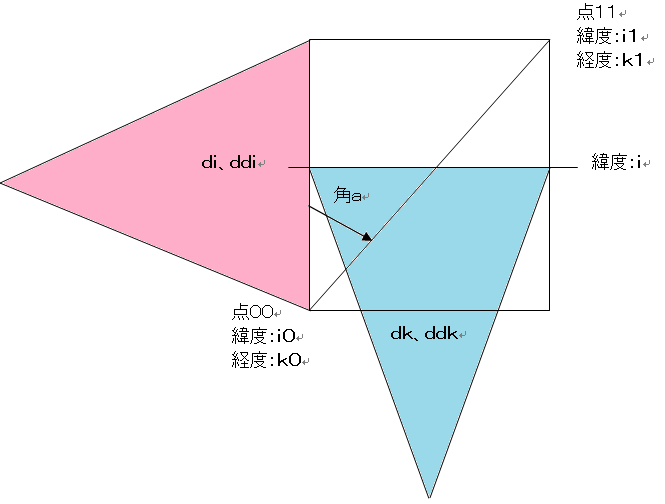
平面座標系と緯度線、経度線
点00緯度(度):i0
点00緯度(ラジアン):I0
点00経度(度):k0
点00経度(ラジアン):K0
点11緯度(度):i1
点11緯度(ラジアン):I1
点11経度(度):k1
点11経度(ラジアン):K1
点00から見た点11の方向(度):a
点00から見た点11の方向(ラジアン):A
目標点距離(m):d
緯度偏移(度):di = i1 - i0
緯度偏移(ラジアン):dI
経度偏移(度):dk = k1 - k0
経度偏移(ラジアン):dK
平均緯度(度):i = (i1 + i0)/2
平均緯度(ラジアン):I
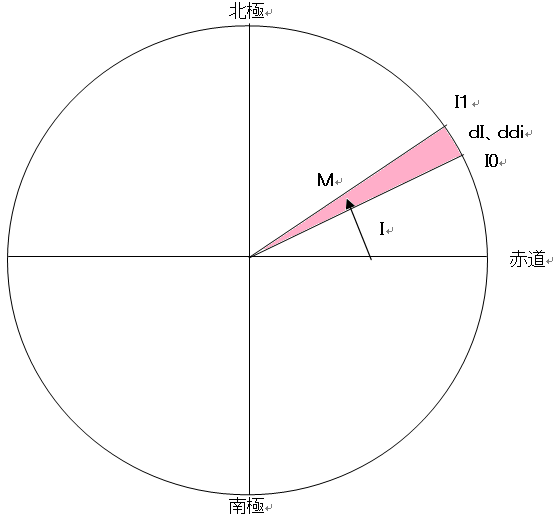
緯度線と子午線曲率半径
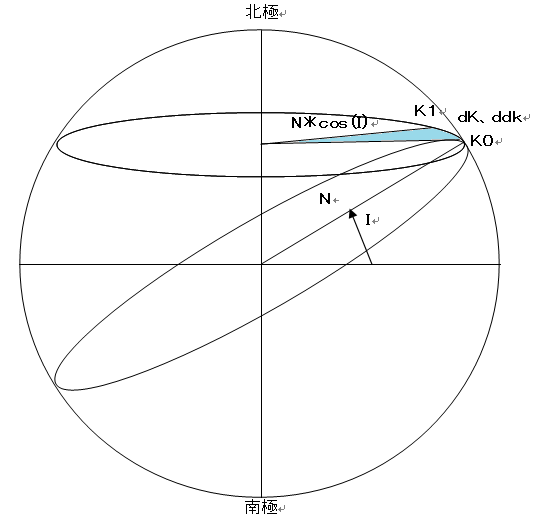
経度線と卯酉(ぼうゆう)線曲率半径
ヒュベニの公式による近似式を用いて
子午線曲率半径(観測点の南北方向大円の近似半径)
M = Rx (1 − E2 )/W^3
卯酉(ぼうゆう)線曲率半径(観測点の東西方向大円の近似半径)
N = Rx/W
子午線・卯酉線曲率半径の分母
W = SQRT(1 − E2*sin(I)^2)
(大円:球の中心を通る円。半径は最も大きくなる。)
WGS84 (GPSで使用する楕円回転体)の定数
(世界測地系で使用するGRS80楕円体との差はわずか)
Rx:赤道半径(m) 6378137.0000000
E2:離心率(e^2) 0.00669437999019758000
とすると、下記の関係が成立するので、相互に変換できる。
緯度方向(南北)の距離 ddi = dI * M
緯度偏移(ラジアン):dI = ddi/M
経度方向(東西)の距離:ddk = dK * N * cos(I)
経度偏移(ラジアン):dK = ddk/(N * cos(I))
2点間の距離(m):d = SQRT((dI * M)^2 + (dK * N * cos(I))^2)
点00から見た点11の方向(ラジアン):A = ATAN(ddk/ddi)
注)
角度、緯度経度の小文字の単位(a,i,j)度、大文字の単位(A,I,K)ラジアン
通常、緯度の表記は、φ、B、lat(itude)、経度の表記は、λ、L、lon(gitude)を使用するが、わかりやすくするために、それぞれ、i、kを用いた。
■ヒュベニの公式
2点間の距離 D = SQRT((Ay * M)^2 + (Ax * N * cos(P))^2)
Ax:2点の経度の差
Ay:2点の緯度の差
P:2点の緯度の平均
M = Rx (1 - e^2 )/W^3:子午線曲率半径
N = Rx/W:卯酉線曲率半径
W = SQRT(1 - E^2*sin(P)^2):子午線・卯酉線曲率半径の分母
e = SQRT((Rx^2 - Ry^2)/Rx^2):第1離心率
Rx:長半径(赤道半径)
Ry:短半径(極半径)
E2 = e^2:第2離心率
■緯度・経度、距離、方位→緯度・経度
2点間の距離(m):d
方位(ラジアン):A
↓
2点の緯度の平均(ラジアン):I = (I0 + I1)/2
2点の緯度の差(ラジアン):dI = d * cos(A)/M
2点の経度の差(ラジアン):dK = d * sin(A)/(N*cos(I))
1.i(2点の緯度の平均)を仮にi0とおいて計算、仮のdi(第1近似)を求める
2.i(2点の緯度の平均)をi0+(仮のdi)/2とおいて再計算(第2近似)
○VBA関数サンプル
Function ido(i0, k0, d, a)
'i0:出発点緯度(度)
'k0:出発点経度(度)
'd:目標点距離(m)
'a:目標点方位(度)
'ido:出発点から距離d(m)、方位a(度)地点の緯度(度)
Pi = Application.WorksheetFunction.Pi() 'π
Rx = 6378137# '赤道半径(m)
E2 = 6.69437999019758E-03 '第2離心率(e^2)
WT = Sqr(1 - E2 * Sin(i0 * Pi / 180) ^ 2) '仮のW(第1近似)
MT = Rx * (1 - E2) / WT ^ 3 '仮のM(第1近似)
diT = d * Cos(a * Pi / 180) / MT '仮のdi(第1近似)
i = i0 * Pi / 180 + diT / 2
W = Sqr(1 - E2 * Sin(i) ^ 2)
M = Rx * (1 - E2) / W ^ 3
di = d * Cos(a * Pi / 180) / M
ido = i0 + di * 180 / Pi
End Function
○VBA関数サンプル
Function keido(i0, k0, d, a)
'i0:出発点緯度(度)
'k0:出発点経度(度)
'd:目標点距離(m)
'a:目標点方位(度)
'keido:出発点から距離d(m)、方位a(度)地点の経度(度)
Pi = Application.WorksheetFunction.Pi() 'π
Rx = 6378137# '赤道半径(m)
E2 = 6.69437999019758E-03 '第2離心率(e^2)
WT = Sqr(1 - E2 * Sin(i0 * Pi / 180) ^ 2) '仮のW(第1近似)
MT = Rx * (1 - E2) / WT ^ 3 '仮のM(第1近似)
diT = d * Cos(a * Pi / 180) / MT '仮のdi(第1近似)
i = i0 * Pi / 180 + diT / 2
W = Sqr(1 - E2 * Sin(i) ^ 2)
N = Rx / W
dk = d * Sin(a * Pi / 180) / (N * Cos(i))
keido = k0 + dk * 180 / Pi
End Function
■2点の緯度・経度→距離、方位
2点の緯度の平均(ラジアン):I = (I0 + I1)/2
2点の緯度の差(ラジアン):dI
2点の経度の差(ラジアン):dK
↓
緯度方向距離差(m):ddi = dI * M
経度方向距離差(m):ddk = dK * N * cos(I)
2点間の距離(m):d = SQRT(ddi^2 + ddk^2)
方位(ラジアン):A = atan2(ddi,ddk)
○VBA関数サンプル
Function Dist(i0, k0, i1, k1)
'i0:出発点緯度(度)
'k0:出発点経度(度)
'i1:到達点緯度(度)
'k2:到達点経度(度)
'Dist:2点の距離(m)
Pi = Application.WorksheetFunction.Pi() 'π
Rx = 6378137# '赤道半径(m)
E2 = 6.69437999019758E-03 '第2離心率(e^2)
di = i1 - i0
dk = k1 - k0
i = (i0 + i1) / 2
W = Sqr(1 - E2 * Sin(i * Pi / 180) ^ 2)
M = Rx * (1 - E2) / W ^ 3
N = Rx / W
Dist = Sqr((di * Pi / 180 * M) ^ 2 + (dk * Pi / 180 * N * Cos(i * Pi / 180)) ^2)
End Function
○VBA関数サンプル
Function Dir(i0, k0, i1, k1)
'i0:出発点緯度(度)
'k0:出発点経度(度)
'i1:到達点緯度(度)
'k2:到達点経度(度)
'Dir:出発点からみた到達点の方位(度)
Pi = Application.WorksheetFunction.Pi() 'π
Rx = 6378137# '赤道半径(m)
E2 = 6.69437999019758E-03 '第2離心率(e^2)
di = i1 - i0
dk = k1 - k0
i = (i0 + i1) / 2
W = Sqr(1 - E2 * Sin(i * Pi / 180) ^ 2)
M = Rx * (1 - E2) / W ^ 3
N = Rx / W
ddi = di * Pi / 180 * M
ddk = dk * Pi / 180 * N * Cos(i * Pi / 180)
a = (Application.WorksheetFunction.Atan2(ddi, ddk) * 180 / Pi + 360)
If (a >= 360) Then a = a - 360
Dir = a
End Function
上記のVBA関数サンプルは下記の範囲で有効
緯度(度):北緯 0〜90、南緯 -0〜-90
南緯i度⇔−(北緯)i度
経度(度):東経 0〜180、西経 0〜-180
西経k度⇔−(東経)k度
極付近の計算で緯度が90度を超える場合と経度180度付近の計算で経度が180度をまたぐ場合以外は正しい結果が得られる。
50km程度までの精度、10^-5程度?
緯度(度)
絶対値が90度を超えた場合
±ABS(180度−i度)、k度→k度+180度(k>180度なら→k度−360度)と解釈する
経度(度)
±180度をまたぐ場合
西経k度⇔東経(360度−k度)と解釈する
以下参考
■精度
ヒュベニの公式:
50km以下ではLambert-Andoyerの公式(10^-5)以下の誤差
Lambert-Andoyerの公式(航海算法):
距離によらず 10^-5 以下の誤差
■カシミールのヒュベニの距離計算式(旧日本測地系:ベッセル楕円体)
Rx * (1 - e^2) = 6377397*(1-0.006674) = 6334834
W = SQRT(1 - e^2 * sin(P)^2) = SQRT(1-0.006674 * sin(P)^2)
M = Rx (1 - e^2)/W^3 = 6334834/SQRT((1-0.006674*sin(P)*sin(P))^3)
N = Rx/W = 6377397/SQRT(1-0.006674*sin(P)*sin(P))
■磁気変移
日本列島における標準的な地磁気分布を表す近似式
D2010.0=7°40.585′+19.033′Δφ-6.265′Δλ+0.009′(Δφ)2+0.024′ΔφΔλ-0.591′(Δλ)2
Δφ=φ-37°N,Δλ=λ-138°E
※φは緯度,λは経度で角度の度単位
■参考URL
○二地点の緯度・経度からその距離を計算する
○カシミール/計算式
○日本列島における標準的な地磁気分布を表す近似式





