用語の説明
・ 慣性系
ニュートンの運動の第一法則が成り立つような系。
・ ニュートンの運動の第一法則
物体に外から力が働かない場合には、初め静止していた物体はいつまでも静止し、運動していた物体は等速直線を続ける。このようにもとの状態を保ち続けようとする性質を「慣性」といい、この法則を「ニュートンの運動の第一法則」又は「慣性の法則」という。
・ 事 象
ミンコフスキー時空図の一点は、時間座標値 t と空間座標値 X がある決まった値をとった点であり、事象とよばれる。
・ 運動量
物体の質量と速度の積は運動の激しさを表わす量と考えられ、これをその物体の運動量という。運動量は一般に速度の方向をもつベクトルである。
・ 正方行列
行の数と列の数が等しい行列。
・ 正則行列
正方行列で行列式の値が≠0である様な行列。
・ 単位行列
対角要素が1で他の要素が全て0である正方行列を単位行列という。


・ 転置行列
行と列を入れ替えた行列。
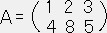
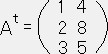 At は転置行列
At は転置行列
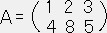
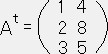 At は転置行列
At は転置行列
・ 逆行列
正方行列Aは正則行列である時に限ってAX=XA=Eである様な行列 X がただ一つ存在する。この様な行列をAの逆行列といい、A-1で表す。即ちAA-1=A-1A=E
・ ベクトル空間
ベクトル空間というのはベクトル空間の公理という次の性質をもつ元(=要素)の集合である。
加法に関して
乗法に関して
ベクトルと名前が付いている為、元がベクトルでなければならないと考え勝ちであるが、
元はベクトルでなくともよい。上記の性質を満足する元の集合はベクトル空間である。
1.二つの元 U,V はただ一つの和 U+V を決定する。
2.結合の法則: (U+V) + W = U + (V+W)
3.交換の法則: U + V = V + U
4.零元 0 が存在して 0 + U = U
5.あらゆる元 U について、- ( U ) + U = 0 であるような元 -U が存在する。
2.結合の法則: (U+V) + W = U + (V+W)
3.交換の法則: U + V = V + U
4.零元 0 が存在して 0 + U = U
5.あらゆる元 U について、- ( U ) + U = 0 であるような元 -U が存在する。
1.一つの元 U とスカラー a
はただ一つの元 aU を決定する。
2.結合の法則: b ( aU ) = ( ba ) U
3.分配の法則: a ( U + V ) = aU + aV ( a + b ) U = aU + bU
4.単位元 1 について 1 U = U
2.結合の法則: b ( aU ) = ( ba ) U
3.分配の法則: a ( U + V ) = aU + aV ( a + b ) U = aU + bU
4.単位元 1 について 1 U = U
・ MCR系
加速度をもって運動している粒子には慣性系(粒子が常に静止して見えるような等速運動をしている系)はない。しかし瞬間的には粒子と同じ速度をもっていて、その時以外は共動していないという慣性系は存在する。この系を瞬間的共動慣性系(momentarily comoving reference frame)、略してMCR系またはMCRFという。
・ 粘性
静止流体が内部で互いに及ぼしあう力は常に圧力である。しかし運動している流体では隣り合う部分の速さが違うと、相手の運動を妨げる力が境界面に沿って働く。これが流体の粘性である。水を入れたコップを静かに回転すると水が周辺から回転し始め、やがて水全体が回転するのは水の粘性のためである。ドロドロした液体などは特に粘性が著しい。
・ 慣性質量と重力質量
ニュートンの運動の第二法則に出てくるのが慣性質量で、万有引力の法則に出てくるのが重力質量である。慣性質量はロケットなどの加速度運動によって引き起こされた力に関係し、重力質量は地球などの天体が原因となって生じた力に関係する。
・ ユークリッド空間
ユークリッド幾何学の場となる平面や空間の事。三次元ユークリッド空間の各点は三つの成分の座標で決定される。「ユークリッド的」という表現は、これらの空間が非ユークリッド幾何学や相対性理論に出てくるような曲がった空間ではない、平らな空間である事を意味している。
・ ユークリッドの平行線の公理
直線外の1点を通って、その直線に平行な直線はただ1本だけ存在する。
・ 非ユークリッド幾何学
ユークリッドの平行線の公理を「直線外の1点を通って、その直線に平行な多数の平行線が引け、三角形の内角の和は2直角より小である」とした幾何学を双曲線の非ユークリッド幾何学という。ユークリッドの平行線の公理を「平行線は全く存在せず、三角形の内角の和は2直角より大きい」とした幾何学を楕円型の非ユークリッド幾何学という。ガウスの弟子のリーマンが始めた幾何学でリーマン幾何学という。
・ デカルト座標
座標軸が直線で直行している座標系の事。
・ 質点
大きさを無視してよい小さな物体。
・ H−R 図
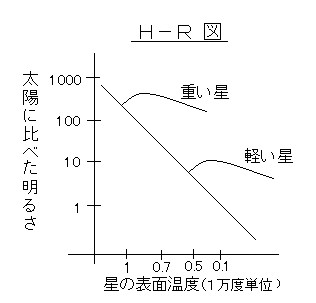 星の表面温度と太陽に比べた明るさの関係をグラフ化したもの。
星の表面温度と太陽に比べた明るさの関係をグラフ化したもの。ヘルツシュプルングとラッセルの頭文字をとってというH−R図という。重い星ほど左上にあり、軽い星ほど右下にある。
・ 超新星爆発
白色矮星の近くに別の恒星があり、そこから水素ガスが降り積もりチャンドラセカール限界質量を超えると炭素と酸素からなる中心核で、炭素の核融合反応が暴走し、Ia型超新星爆発を起こす。
核融合が鉄まで進んだ星では、鉄が高エネルギーのガンマ線を吸収してヘリウムと中性子に分解する(鉄の光分解)。この鉄の光分解は吸熱反応で,僅か0.1秒くらいしかかからず その結果,中心核の圧力が一挙に下がって中心核は潰れ、逆に外層は反動で飛び散る。これがII型超新星爆発である。超新星爆発の仕組みは他にも幾つかある。
核融合が鉄まで進んだ星では、鉄が高エネルギーのガンマ線を吸収してヘリウムと中性子に分解する(鉄の光分解)。この鉄の光分解は吸熱反応で,僅か0.1秒くらいしかかからず その結果,中心核の圧力が一挙に下がって中心核は潰れ、逆に外層は反動で飛び散る。これがII型超新星爆発である。超新星爆発の仕組みは他にも幾つかある。
・ 不確定性原理
一つの粒子の位置と運動量の両方を同時に正確には知る事は出来ないという法則。一方を正確に知れば知るほど、他方を正確に知る事が出来なくなるという原理。これは、真の値があるが人間の能力では正確に知る事が出来ないと誤解されがちであるが、そうではなく、真の値など元々ないというのが物理現象に近い解釈である。
この事は式の上からも言える。不確定性原理の式、△P△X ≧ h に於いて、△P=0なら△Xは無限大になってしまうから。
・ パウリの排他原理
スピン1/2の同種の粒子は(フェルミ粒子)、不確定性原理の設定する限界の中で、同じ位置と同じ速度の両方を持つ事は出来ないという原理。
・ パルサー
パルサーは可視光線、電波、X線等を周期的に規則正しく放射している天体の事で、中性子星がパルサーの正体であると考えられている。パルサーの回転は非常に高速で、しかもきわめて正確なため、人工的な電波のように観測される。この明滅が宇宙人からの信号であると考えられたこともあった。
・ 熱力学の第一法則
これはエネルギー保存の法則である。内部エネルギーの増加△Eは、外から与えられた熱量△Q及び外からなされた仕事の和に等しい。気体の体積増加の時は、外圧のなす仕事P△V(P:圧力、V:体積)は負である。
△E=△QーP△V
△E=△QーP△V