図形描画(マンデルブロー集合)

フラクタル図形の定番のマンデルブロー集合も描画できます。再描画を最低限にしていますので、描画されない場合は付箋のサイズをほんの少し変えてみてください。

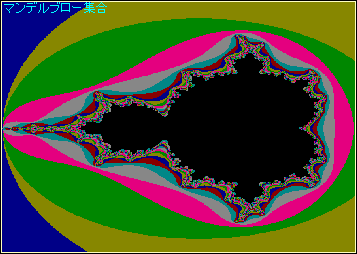
マンデルブロー集合

-- 付箋上にマンデルブロー集合を描画します。
-- 動作が重いので付箋のサイズが変わらない限り
-- 再描画を行わない様にしている。
x = "マンデルブロー集合" 
f_SetTitle("Luaスクリプト:マンデルブロー集合")
gra = f_Graphics()
require('color')
cw = f_GetClientWidth()
ch = f_GetClientHeight()
clist = clist or {
  Brushes.Maroon,
  Brushes.Navy,
  Brushes.Olive,
  Brushes.Green,
  Brushes.Purple,
  Brushes.Gray,
  Brushes.Teal,
  Brushes.Black
}
sw, sh = sw or 100, sh or 100
dx   = 0.005
kmax = 20
xmin = -2.0
xmax = 0.7
ymin = -1.5
ymax = 1.5

pointsizex = cw * dx  / (xmax - xmin) +1
pointsizey = ch * dx  / (ymax - ymin) +1
function drawPoint(x,y, pointcolor)
  local cx = (x-xmin)/(xmax-xmin)*cw
  local cy = (ymax-y)/(ymax-ymin)*ch
  local dx = math.floor((pointsizex + 1)/2)
  local dy = math.floor((pointsizex + 1)/2)
  gra:FillRectangle(pointcolor, cx, cy, pointsizex, pointsizey)
end

function mandelbrot(ptn, a, b)
  dy = dx
  for u = xmin, xmax, dx do
    for v = ymin, ymax, dy do
      x, y = a, b
      k = 0
      d = 0
      while k < kmax and d <= 4 do
        if ptn == 1 then
          zr, zi = (x*x-y*y)+u, (2*x*y)+v
        else
          zr, zi = (x*x-y*y-x)+u, (2*x-1)*y+v
        end
        x,y  = zr,zi
        k = k + 1
        d = x*x + y*y
        if 4 < d then
          drawPoint(u, v, clist[k%8+1])
        end
      end
    end
  end
end

function jikkou(rei)
    if      (rei == 1) then 
      ptn, a, b = 1, 0, 0
    elseif (rei == 2) then 
      ptn, a, b = 1, -.5, -0.2
    elseif (rei == 3) then
      ptn, a, b = 1, 0.2, 0.9
    elseif (rei == 4) then
      ptn, a, b = 1, -0.2, -0.7
    elseif (rei == 5) then 
      ptn, a, b = 2, 0, 0
    elseif (rei == 6) then 
      ptn, a, b = 2, 0.2, 0.7
    elseif (rei == 7) then 
      ptn, a, b = 2, 0.3, -0.8
    elseif (rei == 8) then
      ptn, a, b = 2, 0, 1
    end
    mandelbrot(ptn, a, b)
end

if (sw ~= cw) or (sh ~= ch) then
  f_SetBackColor(Color.Black)
  gra:Clear(Color.Black)
  jikkou(1)
  sw,sh = cw,ch
end