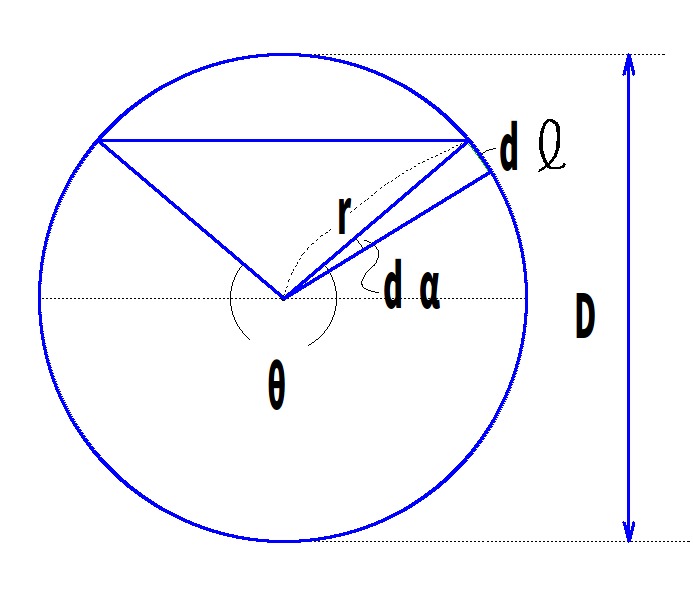
$$流速公式：Q=A\times V,\ \ \ A=\frac{D^2}{8}(\theta -\sin \theta)=\frac{D^2}{8}(2\pi -\sin \pi)=\frac{\pi D^2}{4}$$
(上式の解説はマニング式へ)
$$クッター式：V=\frac{23+\frac{1}{n}+\frac{0.00155}{I}}{1+\left(23+\frac{0.00155}{I}\right)\times \frac{n}{\sqrt{R}}}\times \sqrt{RI}$$ $$（四條畷市都市整備部下水道課Site 掲載の式を参照した）$$ Q：流量（ｍ3/ｓ）