別の部屋になる床パネルどうしが隣あっている箇所があるとします。（１）ここ（白丸）に新たに床パネルを置いたと仮定します。
（２）２つの部屋がつながってしまい、これはルール違反です。
（３）したがって（背理法により）ここには壁ブロックを置かなければなりません。
このパズルを解く有力な方法を一つお教えしましょう。
それは数学でいう「背理法」です。これを使うと、問題が解ける場合がよくあります。
『簡単な例（その１）』
別の部屋になる床パネルどうしが隣あっている箇所があるとします。
（１）ここ（白丸）に新たに床パネルを置いたと仮定します。
（２）２つの部屋がつながってしまい、これはルール違反です。
（３）したがって（背理法により）ここには壁ブロックを置かなければなりません。
『簡単な例（その２）』
３つの壁ブロックが団子状に固まっている箇所があるとします。
（１）ここ（白丸）に新たに壁ブロックを置いたと仮定します。
（２）４つの壁ブロックが正方形状に重なるため、これはルール違反です。
（３）したがって（背理法により）ここには床パネルを置かなければなりません。
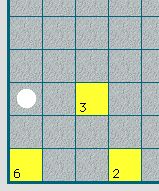まわりを壁や別の部屋の床パネルで囲まれた、数字パネル（図では６）があるとします。
（１）ここ（白丸）に新たに壁ブロックを置いたと仮定します。
（２）最大限に部屋を広げたとしても４マスで指定した数字６には届きません、これはルール違反です。
（３）したがって（背理法により）ここには床パネルを置かなければなりません。
（２）’最大限に部屋を広げたとしても５マスで指定した数字６には届きません、これはルール違反です。
（２）”最大限に部屋を広げたとしても3マスで指定した数字６には届きません、これはルール違反です。
（３）図のように３つの床パネルが確定しました。
そこで、
『もっと一般的にいうと』
最終的にはすべてのマス目に、壁ブロックか床パネルのいずれかのアイテムを置かなければなりません。
ある位置でに床パネルが置けそうだなと思ったら、逆に壁ブロックを置くと（仮定すると）どうなるかを考えてみてください。
これで矛盾が生じる（ルール違反）ならば、それは仮定が間違っていたということですから、仮定と逆のアイテムの床パネルを置くのが正解ということになります。
同様に、壁ブロックを置けそうだなと思ったら、逆の床パネルを置いてみてどうなるかを考えます。
では、もし矛盾が生じないとしたら？ それはまだその位置がアイテムを決定するほど、周囲の環境が整備されていないということです。
そこはとりあえず後の機会にとっておいて、別の位置で考えてみてください。