p=2*l/a/πです。ここまでは普通のビュッフォンの針。
それ以外の時はちょっと複雑です。これが拡張版です。
p = 2*(l+a*arccos(a/l)-sqr(l^2-a^2))/a/πとなります。(詳しくは下の証明)
注:acosはcosの逆関数。
sqrは()内の平方根
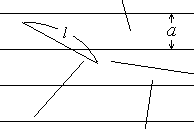
ビュッフォンの針(拡張版)
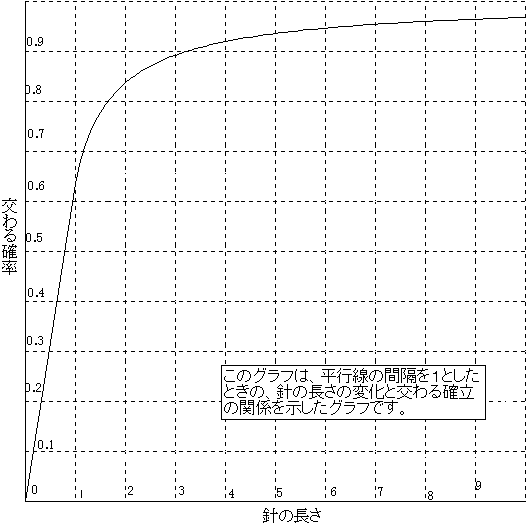
ビュッフォンの針(拡張版)とは、平面上に一定幅[a]に平行線を引き、そこにある長さ[l]の針を落としたときにどういう確率[p]で針と線が交わるかと言うものです。
|
l <= aのときは簡単です。 p=2*l/a/πです。ここまでは普通のビュッフォンの針。 それ以外の時はちょっと複雑です。これが拡張版です。 p = 2*(l+a*arccos(a/l)-sqr(l^2-a^2))/a/πとなります。(詳しくは下の証明) 注:acosはcosの逆関数。 sqrは()内の平方根 |

|
<<証明>>
針の中点から一番近い平行線までの距離をxとおくと、その針が平行線にかかる確率は、
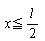 のとき
のとき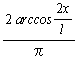 、
それ以外のときは0である。
、
それ以外のときは0である。
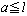 のとき
のとき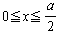 なので、
なので、
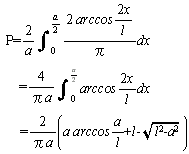 arccosの積分については下図参照
arccosの積分については下図参照
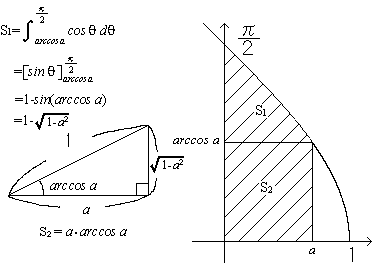
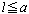 のとき
のとき
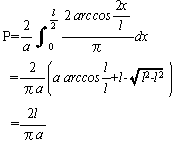
証明終
Copyright © 1998 あっしー All rights reserved.