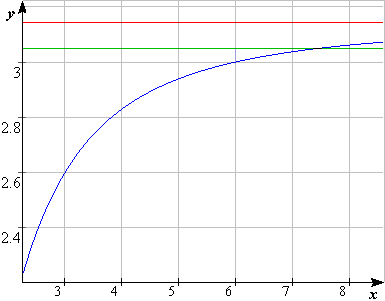
青:y=x角形の辺の長さの和÷2のグラフ(GRAPESを用いて作成)
赤:y=π、緑y=3.05
東京大学の入試問題考
問題はわかりやすいものです。2003年度入試理系数学の6番です
| 円周率が3.05より大きいことを証明せよ |
表記は違いますが、この様な問題です。
昨年は東大卒の社員が会社において実力はあるが 応用力が無いという報道をなされたことを受けてのこと かもしれません。それだけではなく、円周率の計算の 世界的権威は東大の金田教授ですし。
正直、この問題は意外でした。この様な問題にとりくめる 力を持った人に入学して欲しいものです。
ちなみに、私は正8角形の辺の長さの和と円周との比較で 解きました。正7角形ではここまで導けないので、ぎりぎりの 比較です。y=x*sin(pi/x)のグラフ(角形の辺の長さの和÷2)がy=3.05を 越えるのはx=7と8の間なので。(y=3.05はx≒7.47829)
このとき方さえ解れば、中学3年で習う知識(三平方の定理と平方根)で証明は可能です。 チャレンジしてみて下さい。
この方法だと、π>3.06でも証明可能です

Copyright © 2003 あっしー All rights reserved.