2.2 Mini-Max法

前節ではゲーム木について説明しました。 今回は次の手を選ぶ方法として、Mini-Max法を紹介します。 現在の局面から、数手先（図1では３手）の局面をすべて調べ、評価したとします。 この評価値から、どのようにして次の手を選べばよいでしょうか？ この問題を解決する方法として、「Mini-Max法」があります。 これは 相手が自分にとってもっとも不利になるような手を打ってくると仮定して、最善の手を探す 方法です。 図1を見てください。 前節とは違って葉以外の節点にも数字が書かれています。 これは各節点での評価値をあらわし、次の規則に従っています。 節点が自局面のとき その子節点の評価値のうち最大の値 節点が相手局面のとき その子節点の評価値のうち最小の値 赤または青の線は選んだ手をあらわしています。

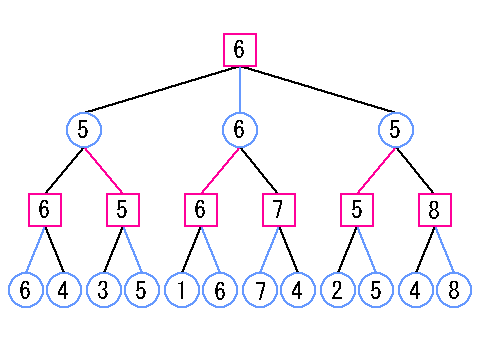図1. Mini-Max法

上の規則に従って下から順に各節点の評価値を決めれば、現在の局面の評価値およびどの手を選択すればよいかが決まります。 具体的には、図2に示す探索手順によって各節点の評価値を決めます。 各節点では次のような処理をします。 節点が葉のとき その時点での局面の評価値をその節点の評価値とし、親の処理に移る 節点が葉以外で、子節点の評価がすべて終わってないとき 未評価の子節点の中から１つ節点を選び、その処理に移る 節点が葉以外で、子節点の評価がすべて終わったとき 節点が自局面のとき 子節点の評価値のうち最大の値をその節点の評価値とし、親節点の処理に移る 節点が相手局面のとき 子節点の評価値のうち最小の値をその節点の評価値とし、親節点の処理に移る C言語の関数風に書くと次のようになります。 ただし、パスがあるときの処理は省略しています。 int mm_max(int t) /* 自局面の節点 tは葉局面までの手数 */ { int max = -N; /* Nは十分大きな値 */ int v; if(t == 0) return (現在の局面の評価値); for(最初の子節点の手; 未評価の子節点がある; 次の子節点に移る){ 局面に子節点の手を打つ; v = mm_min(t-1, alpha, beta); 局面を元に戻す; if(v > max) max = v; } return max; } mm_min(int t) /* 自局面の節点 tは葉局面までの手数 */ { int min = -N; /* Nは十分大きな値 */ int v; if(t == 0) return (現在の局面の評価値); for(最初の子節点の手; 未評価の子節点がある; 次の子節点に移る){ 局面に子節点の手を打つ; v = mm_max(t-1); 局面を元に戻す; if(v < min) min = v; } return min; }

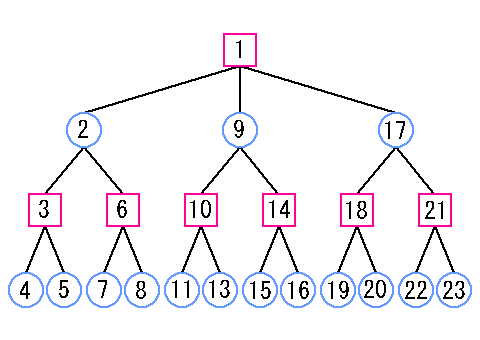図2. 縦型探索での探索手順

図2のように、子節点を優先して探索する手順を「縦型探索」または「深さ優先探索」と呼びます。 これに対し、図3のように、兄弟節点を優先して探索する手順を「横型探索」または「幅優先探索」と呼びます。 横型探索では、目標とする節点（たとえば将棋における詰み）がゲーム木の途中（葉以外の節点）にある場合に有効です。

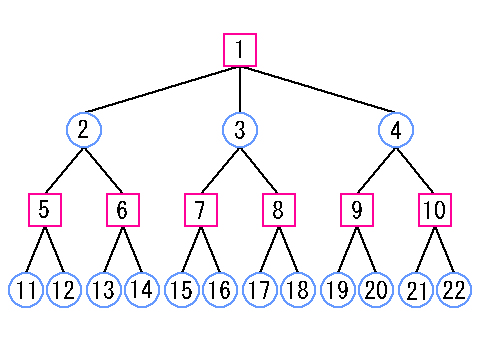図3. 横型探索での探索手順

Mini-Max法では、先読みの手数が増えるごとに、評価しなければならない局面の数が指数関数的に増大します。 そこで、評価する局面を減らすための方法がいくつか提案されています。 次節からは、それらについて説明します。

トップに戻る 2.1 ゲーム木 2.3 Alpha-Beta法