2.3 Alpha-Beta法

今回はMini-Max法を改良した、Alpha-Beta法について説明します。

図1にAlpha-Beta法によって各節点が評価づけられたゲーム木を示します。
説明しやすいように節点に名前をつけています。


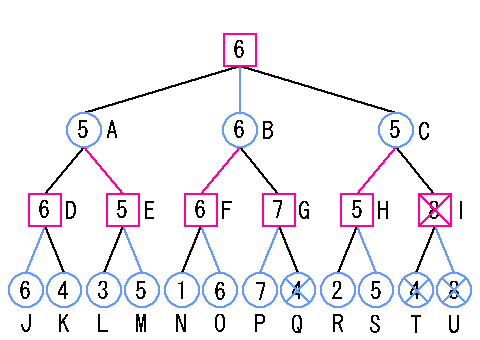Alpha-Beta法
図1. Alpha-Beta法

Alpha-Beta法での探索手順は、Mini-Max法と同じです。
ここでは、図の左側から探索していくとしましょう。

すると、節点Pを探索した後、節点Qは探索する必要がなくなります。
なぜかというと、まず、節点Pの評価値が7なので、節点Gの評価値が7以上になります。
節点Fの評価値は6で、7より小さいので、この時点でBの評価値は6に決まります。
このように、ある節点の評価値がある値以上になるために探索を打ちきることをBeta-cutといいます。

今度は、節点Hを探索した時のことを考えます。
このとき、節点Cの評価値は5以下になります。
すると節点Bの評価値が6なので、節点Cの局面になるような手は採用されないことが決まり、 節点Iより先の探索が打ちきられます。
今度は、ある節点の評価値がある値以下になるために探索を打ちきっています。
これをAlpha-cutといいます。

Alpha-cutおよびBeta-cutによって無駄な探索をしないようにする方法をAlpha-Beta法といいます。
Mini-Max法のときと同様に、各節点での処理を書くと次のようになります。
以下で使用している変数alphaをAlpha値、betaをBeta値と呼びます。

  • 探索の最初
    alpha=-N、beta=Nとし、現在の局面から探索をはじめる。
    （Nは十分大きな値）

  • 節点が葉のとき
    その時点での局面の評価値をその節点の評価値とし、親の処理に移る

  • 節点が葉以外で、子節点の評価がすべて終わってないとき

    • 節点が自局面のとき
      評価済みの子節点の評価値のうち最大の値をalphaに代入する
      alphaがbeta以上のときは、betaをその節点の評価値とし、親節点の処理に移る
      beta以上でない場合は未評価の子節点の中から１つ節点を選び、その処理に移る

    • 節点が相手局面のとき
      評価済みの子節点の評価値のうち最小の値をbetaに代入する
      betaがalpha以下のとき、alphaをその節点の評価値とし、親節点の処理に移る
      alpha以下でない場合は未評価の子節点の中から１つ節点を選び、その処理に移る

  • 節点が葉以外で、子節点の評価がすべて終わったとき

    • 節点が自局面のとき
      子節点の評価値のうち最大の値をその節点の評価値とし、親節点の処理に移る

    • 節点が相手局面のとき
      子節点の評価値のうち最小の値をその節点の評価値とし、親節点の処理に移る

Mini_Max法のときのようにC言語の関数風に書くと次のようになります。
これもパスがあるときの処理は省略しています。

int ab_max(int t, int alpha, int beta) /* 自局面の節点での処理 tは葉局面までの手数 */
{
  int v;

  if(t == 0)
    return (現在の局面の評価値);

  for(最初の子節点の手; 未評価の子節点がある; 次の子節点に移る){
    局面に子節点の手を打つ;
    v = ab_min(t-1, alpha, beta);
    局面を元に戻す;
    if(v > alpha){
      alpha = v;
      if(alpha >= beta)
        return beta;
    }
  }

  return alpha;
}

ab_min(int t) /* 相手局面の節点での処理 */
{
  int v;

  if(t == 0)
    return (現在の局面の評価値);

  for(最初の子節点の手; 未評価の子節点がある; 次の子節点に移る){
    局面に子節点の手を打つ;
    v = ab_max(t-1, alpha, beta);
    局面を元に戻す;
    if(v < beta){
      beta = v;
      if(beta <= alpha)
        return alpha;
    }
  }

  return beta;
}

次節からは、さらに効率よく探索するための工夫について説明します。


トップに戻る
2.2 Mini-Max法
2.4順序付けと反復深化法