|
この章では、局面の評価の方法について説明します。
ここでいう評価とは、ある局面が与えられたときに、そこから1手も進めることなしにどちらがどれだけ有利かを調べることです。
これを静的評価と呼びます。
評価値を計算する方法として、もっともよく使われるのは、局面におけるパラメータに重みをつけて和をとることです。
例えばx,y,zであらわされるパラメータがあったら、wx,xy,zzを重みとして、評価値vは
v = wxx + wyy + wzz
で表されます。
重みはゲームの段階(空きマスの数)によって変化させることもあります。
では評価に使われるパラメータには、何があるでしょうか。
- 着手可能手数
自分および相手が石を置けるマスの数がいくつあるかという値です。
打てる場所が少ないプレイヤーは、石の置ける場所をコントロールされやすくなり、
ひどい場合には置きたくない場所(例えば隅のとなり)に石を置かざるを得なくなります。
そのため、オセロにおいてはもっとも重要なパラメータです。
これを求めるためのもっとも単純な方法は、マス1つ1つに石が置けるかどうかを調べることです。
しかしこの方法には、時間がかかるという欠点があります。
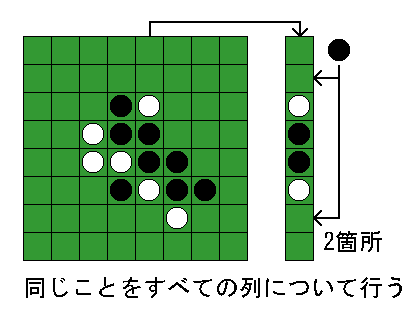
その問題を解消するために、縦横斜めの各列について、それぞれのパターンに対して石を置ける場所がいくつあるかを調べるという方法があります(図1)。
この方法では着手可能な場所を重複して数える可能性があります。
例えば上方向と右方向に石を返せる場所があったときに、それを2箇所として数えてしまいます。
しかし、この近似値を使用しても特に問題はないと思います。
|
| |
図1. 着手可能手数を調べる様子
|
|
- 確定石
終局まで返ることのない石の数です。
これも正確な値を求めるのが困難であり、またその必要もないので、近似値を使用します。
例えば、隅に石があった場合に、そこから何石同色の石が連続しているかを調べます。
- 辺
辺の形に対する評価はかなり難しいと思います。
一つの方法として、いくつかの辺の形についての評価値をあらかじめ決めておくやり方があります。
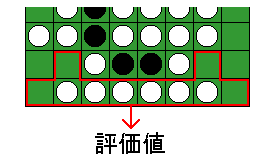
例えば、辺の1列とそれに接する星2つのパターンに対する評価値をすべて登録しておき、それと対象の局面とを比較します(図2)。
|
| |
図2. 辺の評価の例
|
|
- 開放度
開放度理論とは、村上九段と宮崎四段が初心者のために中盤の考え方を定量的にわかりやすく示した理論です。
ある手に対し、返した石の周囲にいくつの空きマスがあるかで定義され(石を置いた場所は空きマスとみなす)、この値が小さい方が良い手とされています。
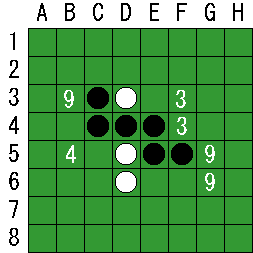
図3を例にして考えてみます。
現在白番です。
B3の手はC3とC4の石を返します。
C3の周囲には空きマスが5個、C4の周囲には空きマスが4個あるので、開放度は9です。
同様にして、図に書かれている開放度が求められます。
何手か先を読む場合には、自分が打った手の開放度の和から相手が打った手の開放度の和を引いた値を使用します(何手先かによって重みを変えることも考えられる)。
|
| |
図3. 開放度の例
|
| |
|
| トップに戻る
3.2 パターンによる評価
| | | |