四次元図形の入門は正多胞体の図を描くことである。
そのためには、まず、各正多胞体の各頂点の座標を求める必要がある。正多胞体の頂点の座標はいくつかの本に書かれている。代表的なものとして、以下がある。
1、宮崎興二、石原慶一。4次元グラフィックス。朝倉書店、1989。ISBN 4-254-10075-2
2、宮崎興二、小高直樹。図形科学。朝倉書店。ISBN 4-254-20103-6
3、一松信。高次元の正多面体。日本評論社、1983。
普通は、正多胞体を四次元空間で回転させた後、単純にu座標を無視して四次元超平面、つまり三次元空間に平行に投射し、さらに3D表示する。
しかしここでは、前節で導入した四次元版平射図法地図を活用する。図形はかなり歪むのだが、四次元球表面の全体が見渡せるので、多面体の絡みなどが理解しやすい、と思えるからである。おそらく、どの点を結んだのが正多胞体の辺になるのか、面になるのか、体になるのかが分かりやすくなると思う。
平射図法で超南極(0, 0, 0, -1)に視点を置き、超北極(0, 0, 0, 1)を投射後の原点に持ってくるように地図投影する。地図投影であるから四次元単位球面から三次元ユークリッド空間への写像である。だから、多胞体の頂点は正確な位置を反映しているが、辺や面や体は超球面に膨らんだ後の姿を投影することになる。しかし球面に投影された角度が分かるほうが便利なこともあり、誤解の恐れを帳消しにできるほどの利点があると思う。
代表点の座標の対応は、
| 地点名 | 四次元座標 | 地図上の点(三次元) |
| 超北極 | (0, 0, 0, 1) | (0, 0, 0) |
| 超南極 | (0, 0, 0, -1) | なし(無限遠) |
| 北極 | (0, 0, 1, 0) | (0, 0, 1) |
| 南極 | (0, 0, -1, 0) | (0, 0, -1) |
| 以下、超赤道上、赤道上 | ||
| 経度0度 | (1, 0, 0, 0) | (1, 0, 0) |
| 経度90度 | (0, 1, 0, 0) | (0, 1, 0) |
| 経度180度 | (-1, 0, 0, 0) | (-1, 0, 0) |
| 経度-90度 | (0, -1, 0, 0) | (0, -1, 0) |
つまり、地図の原点を中心とする単位球面上の点はu座標が0の球面で、投射後も不動である。地図の単位球面の内部を原点に向かって、u座標が0から1まで超球面上をせり上がり、地図の単位球面から無限遠に向かってu座標が0から-1に超球面上を沈んでゆく。
地図の単位球面は、四次元超球面の超赤道(u = 0)である。赤道(z = 0)は一次元の円ではなく二次元の球面であり、地図上ではZ
= 0の平面に投射される。経度0度(y = 0)の超球面上の地点も(裏の経度180度の地点も含めると)二次元の球面であり、地図上のY
= 0の平面に投射される。同様に、経度±90度(x = 0)の地点も四次元超球面上の二次元の球面であり、地図上のX
= 0の平面に投射される。
これら4つの二次元の球面は四次元超球面(四次元内の三次元図形)を半分に分割する位置にあり(つまり三次元球面の大円に相当する)、超球面上で互いに直交している。その様子を三次元人の我々が直接想像するのは、いささか困難だが、上述の地図に展開すると、3枚の互いに直交する原点を通る平面と、単位球面に写像されるから、少し分かりやすくなるのではないだろうか。コンピュータグラフィックスにして四次元内を回転させると、すべての球面が(大きさは異なるかもしれないが)球面に写像されるので、感じが出ると思う。

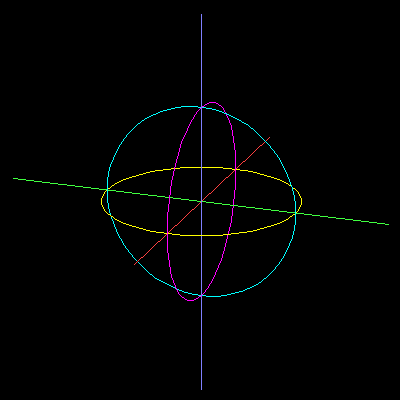
上図はお手軽にVisual BASICに描かせた地図である(3D表示が正射影なので奥行きが分かりにくいと思う)。3つの楕円は三次元空間内の円のつもりで中心からの距離が1の単位円である。赤がX軸で、図の左下が手前のつもりで、Xの正の方向である。マゼンタ・黄色の円と交わっているところが(1, 0, 0, 0)の点で、超赤道上・赤道上の経度0の点である。緑はY軸で、図の右が正の方向である。同じく、黄色・シアンの円と交わっているところが(0, 1, 0, 0)の点で、超赤道上・赤道上の経度90の点である。青はZ軸で、図の上が正の方向、シアン・マゼンタの円と交わっているところが(0, 0, 1, 0)であり、(超赤道上の)北極である。3軸の交わっている原点は超北極(0, 0, 0, 1)である。超南極(0, 0, 0, -1)は方向不定で無限のかなたである。
● 正5胞体
正5胞体は非常にとがった図形なので、正射図法にしても平射図法にしても、うまく表現できない。幸い、図形としては単純なので、座標入力に苦労することはないであろう。
上述の文献2の座標の導出方法が最も単純である。各座標軸の1の点、つまり、(1,
0, 0, 0)、(0, 1, 0, 0)、(0, 0, 1, 0)、(0, 0, 0, 1)が正四面体を形作っているので、あと一点を加えればよい。これら4点の互いの距離はsqrt(2)(≒1.4142...)なので、これら4点からの距離がsqrt(2)になる点を取ればよい。対称性から(a,
a, a, a)の形をしていて、幸い、二次元の作図によって簡単に座標が計算できる。そのような点は原点方向と反対方向に2つあり、原点方向の点の座標は((1-sqrt(5))/4,
(1-sqrt(5))/4, (1-sqrt(5))/4, (1-sqrt(5))/4)である。この座標の出し方では正5胞体の中心は原点から外れてしまい、((5-sqrt(5))/20,
(5-sqrt(5))/20, (5-sqrt(5))/20, (5-sqrt(5))/20)の位置にある。頂点のどのペアをとっても辺で結ばれているので、図形を描くには苦労しないと思う。
ちなみに、この座標導出法は5次元以上の正単体にも適用できて、nを次元とすると、上述の(1/sqrt(5))/4に相当するのは(1-sqrt(n+1))/nで、(5-sqrt(5))/20に相当するのは(n+1-sqrt(n+1))/(n*(n+1))である。どの次元でも辺の長さはsqrt(2)である。
● 正8胞体 (超立方体)
最も簡単な四次元図形の一つで、四角い置き物の感じであろう。頂点は16あり、(1,
1, 1, 1)、(-1, 1, 1, 1)、(1, -1, 1, 1)、(-1, -1, 1, 1)、(1, 1, -1, 1)、(-1,
1, -1, 1)、(1, -1, -1, 1)、(-1, -1, -1, 1)、(1, 1, 1, -1)、(-1, 1, 1, -1)、(1,
-1, 1, -1)、(-1, -1, 1, -1)、(1, 1, -1, -1)、(-1, 1, -1, -1)、(1, -1, -1,
-1)、(-1, -1, -1, -1)とすればよい。中心は原点(0, 0, 0, 0)である。
二進法が好きな人は、(0, 0, 0, 0)、(0, 0, 0, 1)、(0, 0, 1, 0)、(0, 0,
1, 1)、(0, 1, 0, 0)、(0, 1, 0, 1)、(0, 1, 1, 0)、(0, 1, 1, 1)、(1, 0, 0,
0)、(1, 0, 0, 1)、(1, 0, 1, 0)、(1, 0, 1, 1)、(1, 1, 0, 0)、(1, 1, 0, 1)、(1,
1, 1, 0)、(1, 1, 1, 1)でもよい。中心は(1/2, 1/2, 1/2, 1/2)である。
上述の地図でも簡単である。x, y, zの各座標が0になる平面とuが0になる単位球面で三次元ユークリッド空間が16に分割される。元の四次元超球面では、16の直角超球面正四面体に相当する。この各超球面正四面体の中心が超立方体の頂点になっている。地図では各部屋の中心に相当する点に頂点を打点すればよい。実際にプロットしてみれば、辺を結ぶのも簡単であろう。
● 正16胞体
この図形はさらに簡単である。先に挙げた地図の図形そのものである。
頂点の位置は(1, 0, 0, 0)、(-1, 0, 0, 0)、(0, 1, 0, 0)、(0, -1, 0, 0)、(0,
0, 1, 0,)、(0, 0, -1, 0,)、(0, 0, 0, 1)、(0, 0, 0, -1)に取ればよく、地図では、(1,
0, 0)、(-1, 0, 0)、(0, 1, 0)、(0, -1, 0)、(0, 0, 1)、(0, 0, -1)、(0, 0,
0)、無限のかなた、つまり表の各極である。辺は各座標軸上に4本ずつ(-∞〜-1,
-1〜0, 0〜1, 1〜∞)、原点を中心とする単位円とXY, YZ, ZX平面との交点の円上に4本ずつ(90度ずつ)の24本ある(ただし、超球面上へ投影されたものだが)。面と体も自明であろう。正8胞体のところで述べた16の超球面正四面体は、正16胞体を覆う16の正四面体が中心から球面に投影された結果である。
● 正24胞体
平射図法表現が特に役立つ図形である。正16胞体の辺の中点を頂点とすればよい。上述の表の8つの極から45度ずつずれた辺上の位置に頂点がある
それぞれの8つの極を中心として正八面体が構成できる。この八面体の1/8が正16胞体のそれぞれの正四面体の頂点から食い込んでおり、切頭操作で正八面体が残る。言葉では分かりづらいかもしれないが、図示すると一目瞭然である。
対称性の高い立体であるので、四次元内の回転をアニメ化すると、もっと別の表現ができるかもしれない。

正24胞体の表面の正八面体の一つ
● 正120胞体
正直申し上げよう。頂点が600もあるので、まだ直感的に頂点配置が思い浮かばない。幸いにして正600胞体(双対図形)の各正四面体の中心を頂点とすればよいので、次項を見れば計算はできると思う。
(次のページに直感的配置を掲載した(2002-9-21))
● 正600胞体
地図表現がありがたく思える立体。分かってしまえば意外に簡単(?)である。
120の頂点のうち、16は上述の正8胞体の頂点、8つは正16胞体の頂点と同じ位置にある。
残りは、(±τ, ±1, ±τ-1, 0)の偶置換とのこと。ここでτ(タウ)は黄金比((1+sqrt(5))/2 ≒1.618...)で、-1は逆数(1/x)を表す。偶置換とは要素の置き換えを偶数回行った結果のことで、この場合(A
B C D), (A C D B), (A D B C), (B A D C), (B C A D), (B D C A), (C A B D),
(C B D A), (C D A B), (D A C B), (D B A C), (D C B A)の12パターンのことである。3つの±で8通りだから、結局残りの96点が尽くされている。ただし、原点からの距離が2であるので、最終的には距離を半分にしないといけない。
要素の一つが0であるから、地図上のXY, YZ, ZXの各平面と単位球面上に96(+8)の頂点がある。
下の図は正600胞体の三次元地図のXY平面を取り出したものである。中心が超北極(0, 0, 0, 1)である。直交する黒の2直線は、横がX軸で、縦がY軸である。Z軸は図と直角方向の前後に延びているので見えない。黒の円はu=0の球面がXY平面に交わっている所である。黒の円と黒の横線が交わっている点の座標は、右が(1, 0, 0, 0)、左が(-1, 0, 0, 0)である。黒の円と黒の縦線が交わっている点の座標は、上が(0, 1, 0, 0)、下が(0, -1, 0, 0)である。
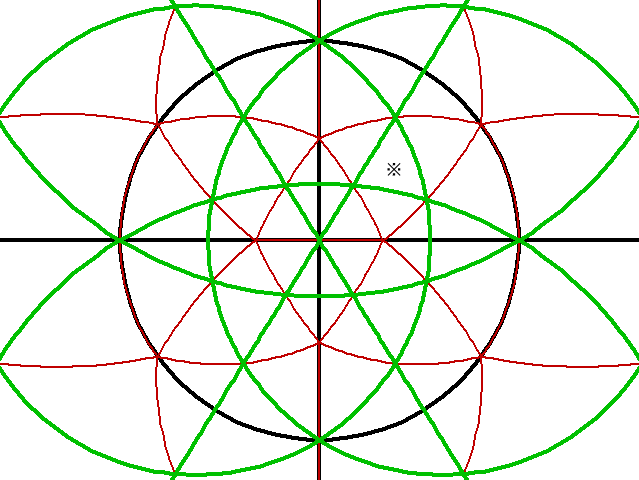
緑は正600胞体の辺(の超球面への投影)が、たまたまXY平面に乗っている部分である。曲線の三角形に見える部分は、元はすべて同じ大きさの正三角形であり、向こうとこちら側に2つの正四面体が合わさっている部分である。
右上の1/4円の中央部に少し右に傾いた緑の三角が認識できると思う(※のある三角形)。この三角の左下の頂点の座標は(τ-1, 1, 0, τ)、右下の頂点は(τ, τ-1, 0, 1)、上の頂点は(1, τ, 0, τ-1)である。この三角形の各々の頂点と(1, 1, ±1, 1)を結ぶと(2つの)正四面体になる。
赤い線は、正四面体の面(の投影)とXY平面が交わっている部分である。XY平面が正四面体を半分に分けていて、赤2本と緑(辺)1本の三角形は正四面体(の投影)の断面である。だから、赤の線が5本集まっている場所からZ方向の前後に正四面体の他の頂点がある。
上図はZ=0のXY平面のつもりで描いたものだが、他にX=0のYZ平面, Y=0のZX平面,
U=0の単位球面でも同様の図が描かれる。一つの図には20の正三角形が描かれているので前後で40の正四面体が乗っており、4面で160の正四面体が識別される。
一つの図に五角形は12あり、それぞれ5つの正四面体を半分に分けている。重複を除くと、4面で結局120の正四面体が加わることになる。
その結果、600 - 160 - 120 = 320個の正四面体が図から浮いていることになる。
無理に想像をたくましくして浮いている正四面体を考えてもよいのだが、こんな場合はあきらめて模型を作ってみるのが安全確実であろう。上述のVisual
BASICのプログラムをいろいろ改造してみた。
※の正三角形上の正四面体と面を共有する正四面体が、あと3つ取れる。それぞれの正四面体の残りの頂点は、他の面上にある。したがって、重複は無く、3
* 4 * 16 = 192個の正四面体が識別される。
残る正四面体は、各極(「極の表」の8点)と、極を結ぶ4面で区切られた16の直角超球面正四面体の中心(たとえば※の正四面体の最後の頂点)を結ぶ線上に2個ずつある。極に近いほうの正四面体の3辺はZ=0の面等に乗っているが、もう一方の正四面体は点でしか接していない。このグループの正四面体の数は2
* 4 * 16 = 128なので、これですべての正四面体が網羅された。
▼ アリシア胞 (捩れ24胞体)
良い機会なので捩れ24胞体とも呼ばれる半正多胞体、アリシア胞の構成を見てみよう。「四次元半正多胞体」のところで述べた構成が、そのまま上図で確認できる。
まず、各極を中心として8個の正二十面体がある。各極には20個の正四面体が集まっているので、それらをくっつけてしまうと正二十面体の出来上がりである。三次元空間でたとえると、正三角形5枚でできた薄い正五角錐(側面のみ)を押しつぶして正五角形にした感じである。
※の正三角形上の正四面体のもう一つの頂点は、周囲の4極から等距離の点、つまり上で述べた超立方体の頂点にある。ここにも20個の正四面体が集まっているので、くっつけると、全体で16個の正二十面体ができる。
つまり、8 + 16 = 24個の正二十面体が隣の8つの正二十面体と正三角形で面しながら、超球状の立体(アリシア胞)を網目状に覆っているのである。もちろん、対称性から正24胞体の正八面体と同じ配置になる。模型を作るとすぐに分かるが、この正二十面体は正八面体に内接している。
超球面の残りの空間に対応して、600 - (24 * 20) = 120個の正四面体が塞いでいる。上図において、緑の三辺で囲まれた三角に対応する正四面体と、浮いている正四面体は正二十面体への合体のために使い果たしてしまった。だから、残りの120個の正四面体のすべては上図の緑と赤二本で囲まれた三角のどれかに該当するはずである。
まず、図の中心の超北極のすぐ上の緑で囲まれた三角の、すぐその上の正四面体の断面に注目してみる(黒の線が中心を走っている)。この正四面体は、極が中心の正二十面体の2個と辺で接し、正8胞体の頂点を中心とする正二十面体の4個と辺で接している。この正四面体と同じ立場の正四面体の中心は、上で述べた正24胞体の頂点と一致しているので、24個の正四面体が識別できたことになる。
図ではその両脇の、たとえば※の三角との間の正四面体の断面が、残りの正四面体である。一面が正24胞体の頂点の正四面体と面し、一面が極を中心とする正二十面体に面し、二面が正8胞体の頂点を中心とする正二十面体に面している。数を数えてみるとちょうど96個になるので、これでアリシア胞の構成が完成した。
2002年9月12日 岡田好一