頂点を共有する、正十二面体、立方体、正四面体
前ページ(「正多胞体の座標」)の書き込みから一週間ほど考えていたのだが、頭の中の回転では正120胞体の直感的な座標がどうしても浮かばなかったので、実体模型を作ってみることにした。
とはいえ、模型を作るまでに手をこまねいていた訳ではない。
正120胞体の頂点は600個ある。正120胞体は正600胞体の双対図形であるので、単に表示する目的なら、前出の正600胞体の構成が分かっているので、簡単に頂点座標やその結びつきが計算できる。
ところが、正120胞体を四次元空間内で適当に回転させると、その600の頂点が、正600胞体の120個の頂点をすべて網羅してしまう、という驚くような事実がある。そのとき、同じ頂点を共有する正120胞体と正600胞体がどのように絡んでいるのか、興味が湧いてきてしまった。
むろん、このような単純な疑問は、とっくに誰かが解決して発表しているはずである。実際、具体的な座標は文献に書いてある。しかし、私の探索範囲では分かりやすい図は見られなかった。
この手の図形の操作に慣れてくると、面白いもので、上述の事実から直ちに、以下のような図形が思いつく。

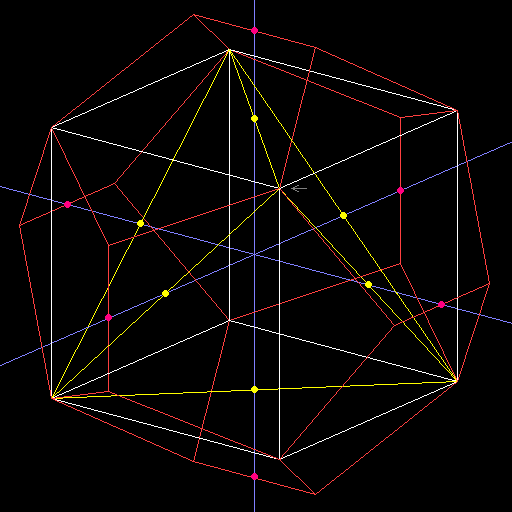
頂点を共有する、正十二面体、立方体、正四面体
かなり線が重なってしまった。まず、青色は手がかりのための座標軸である。右上から左下へ向かってX軸の正の方向、左上から右下に向かってY軸の正の方向、下から上に向かってZ軸の正の方向である。
黄色は正四面体で、正600胞体の体の一つのつもりである。赤は正十二面体で、正120胞体の体の一つのつもりである。白はいわゆる補助線で、立方体が見えると思う。黄色とピンクの丸点は、座標軸との交点である。
原点のやや上、少し右に赤・白・黄色の辺が3本ずつ集まっている点(灰色←)があり、この座標は(1/sqrt(3),
1/sqrt(3), 1/sqrt(1))である。つまり、外接球の半径は1である。正十二面体の他の頂点の座標は、sqrt(10+2*sqrt(5))/4と(sqrt(5)-1)/4と0の適当な組み合わせである。
この図は思い付きであるので、正しいかどうかを計算する必要がある。幸いにも辺の比率は計算と一致した。つまり、超外接球の半径を一致させた場合、正120胞体を構成する正十二面体の辺を三つたどれば、直径が同じ正600胞体の体である正四面体の辺の他の端にたどり着く。
さらに幸運なことに、この図形は最終的な正120胞体と正600胞体の配置にそのまま出現する。
さて、頭の中で構成できたのは、ここまで、であった。要は、この図形の周辺の様子が分からないのである。そこで、以下のような実体模型を作成してみた。

作品名「正120胞体と正600胞体の絡みの中心部」
2002-9-21 岡田好一
ストローで正十二面体を構成し、頂点をタコ糸で結んで正二十面体を作っている(右下の赤の正十二面体の中には糸の立方体もある)。ストローの正十二面体は中心点に4つ集まっていて、隣の立体と面を共有している。なんとなく歪んで見えるが、気のせいではないし、そもそも三次元空間内では歪なしに組み立てることはできない。糸がたるんでいるのも、作りのせいもあるとは思うが、歪のせいでもある。
本来なら、正120胞体と正600胞体の三次元への投影を考え、投影後の距離関係で模型を作るべきであろう。しかし、本模型の目的は、座標の算出ではなく、正十二面体と正四面体がどう絡んでいるかを見るだけなので、お手軽に作ってしまった。
● 実体模型の作り方
準備。ストローとタコ糸とセロハンテープを用意する。ストローはミニサイズ(133mm)が扱いやすい。百円ショップを活用すれば、材料費は300円程度であろう。製作時間は約3時間である。
写真の立体はセロテープでのみで角度を付けているが、しっかりやるなら針金等で頂点部を補強すべきであろう。
(1) まず、ストローで最初の正十二面体を作る。
(2) 糸で上図の位置関係の正四面体を作る。いきなり作るのが困難なら、最初に立方体を張っておけば手がかりになる。糸の長さは、ストロー(正十二面体の辺長)に対し、立方体の一辺が(sqrt(5)+1)/2倍、正四面体の一辺がさらにそのsqrt(2)倍である。作品の場合、ストローが133mmなので、立方体の一辺は215mm、正四面体の一辺は304mmである。模型を作れば分かるが、少々長めに糸を作っておくとよい。
(3) 正四面体の頂点の一つに正十二面体の頂点が集まるように、正十二面体をストローで3つ追加する。
(4) 立体の中心に正二十面体の中心が来たと想定し、正四面体を面で折り返した位置に、次々に正四面体をタコ糸で付け加えてゆく。
(3)と(4)の操作は四次元では少々角度を付ければうまく行くが、三次元ではどこかに無理が生じてしまう。図形のごく中心部のみの再現なので理屈では「多少」の歪のはずだか、明らかに見えてしまうほどの歪であった。
● 実体模型から分かったことは
[1] 正十二面体の内部にある(正600胞体を覆う)正四面体の内部には正120胞体の頂点は一つもない。正120胞体の辺も面も含まない。正120胞体を覆う正十二面体はもちろん120個あるから、この第一型の正四面体も120個ある。一つの頂点に4つの第一型の正四面体が集まっている(面も辺も互いに共有しない)。第一型の120個の正四面体だけで正600胞体の頂点はすべて使われている。
[2] 残りの480個の正四面体はすべて同型(第二型)で、内部に1つの正120胞体の頂点を持つ。正120胞体の1本の完全な辺と、3本の半分の辺が内部の頂点に集合している。完全な辺のもう一つの端は正四面体の頂点の一つにある。半分の辺を延長すると、面で隣り合う他の第二型正四面体の内部頂点に達する。このことから、第二型の480個の正四面体は面でつながって正600胞体を網目状に覆う。この四面体には正十二面体の面が含まれているのだが、その切れ方はやや複雑であり、かつ、立体の構成にはあまり役立たない情報と思えるので、計算機内部に立体を構成するまでお預けとしよう。
正十二面体の頂点は正四面体の頂点と一致するかどうかで2種類に分けられる。写真の模型は集まっている方の頂点を中心としている。中心の頂点には正四面体が20個集まっていて、中心の頂点と反対側の正三角形は正二十面体を構成する。また、中心の頂点には[1]で述べた第一型の正四面体4個と[2]で述べた完全な辺が4つ集まっている。正十二面体の20個の頂点の中で、「中心の頂点」は4個ある。
● 全体の構成
以上は頂点周りの局所の様子である。であるから、全体の構成が具体的に可能であることを示しておきたい。
理解には「正多胞体の座標」のページで最後に述べたアリシア胞の構成が役立つ。実際には正600胞体の120の頂点すべては上述の「中心の頂点」であるのだが、実用上は適当に「グループ分け」するほうが理解しやすくなる。
アリシア胞には正四面体が120個と正二十面体が24個あったことを思い出そう。正600胞体は、その正二十面体を抜いて、20個ずつの正四面体で埋めなおすと構成できる。正600胞体表面の単位超球面(x2+y2+z2+u2 = 1)への投影からの平射図法地図のXY平面を抜き出した図を再掲する。
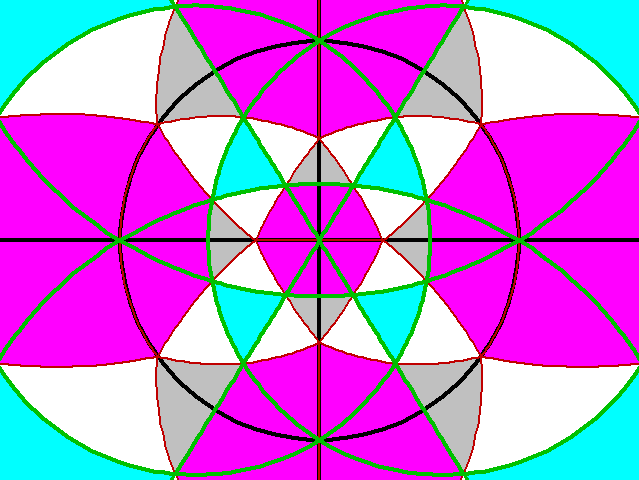
正600胞体を基にしたアリシア胞の構成
この図はXY平面(x2+y2+u2 = 1 & z=0)を意図したもので、同等の面は他に3枚(x=0, y=0, u=0)ある。横の黒線がX軸(z=0
& y=0 & x2+u2 = 1)で、縦の黒線がY軸(z=0 & x=0 & y2+u2 = 1)、黒の円が超赤道との交わり(z=0 & u=0 & x2+y2 = 1)である。緑の線は正600胞体の辺の超球面への投影が直接XY平面に乗っている場所である。赤線は超球面に投影された正600胞体の表面の正四面体の面とXY平面の交わりで、XY平面が正四面体を(図の上下に)半分に分けている(図の詳しい解説は「正多胞体の座標」を参照してほしい)。
アリシア胞の正二十面体は、上図の極(黒い線の交点)を中心とした8個(マゼンタの部分)と、シアン色の三角形を表面とする16個がある。
極を中心とする20個の正四面体の中で8個は4枚の図から浮いている。極を中心とする、この8個の正四面体のうち、隣り合わない4個の正四面体を上述の「第一型」と置く(置き方は興味深いことに右向きと左向きの二種がある)。
極からその正四面体の中心の方向へ直線(四次元球面上の測地線)を延長すると、極を頂点とする大きな直角球面正四面体の中心(それはシアン色の三角形を表面とする正二十面体の中心でもある)を通り、さらに別のシアン色の三角形の中心を通り、結局12個の正四面体を貫いて元に戻る、つまり大円になる。このとき、大円に沿って第一型の正四面体と第二型の正四面体が交互に現れるように配置されている。アリシア胞の正二十面体の表面の様子を一定にするように第一型の正四面体を配置すると、すべてのアリシア胞の正二十面体に対応する正四面体には、結局4*(8+16)
= 96個の第一型正四面体と、384個の第二型正四面体が識別される。
アリシア胞から24個の正二十面体を取ると、120個の正四面体が残る(図の白と灰色の部分)。図の中心は超北極(0,
0, 0, 1)であるのだが、そのすぐ上に頂点を下にした緑の球面正三角形がみえる。そのすぐ上、緑と赤二本の線で囲まれた二等辺三角(中心を黒い線が貫いている灰色の三角)を含む正四面体が、残りの24個の第一型正四面体の一つである。この正四面体に面で隣り合う正四面体(図では白色)は4個あり、いずれもアリシア胞の正四面体に属しており、こちらは第二型の正四面体で、全体で96個ある。これで正600胞体の正四面体は網羅されたことになる。
面白いことに、上述の第一型、第二型の正四面体を6個ずつ交互に中心を貫く大円は、アリシア胞の正四面体のみを使っても描くことができ、全体で16本引くことができる。正四面体でなく、正十二面体で言うと、6つずつの辺と正十二面体が交互に連なったネックレスのようになっている。(なお、ここで述べた大円は、超球面上に投影したときにできるもので、元の立体では取れない。配置の直感の助けになるので説明した)
● 補足
上記の説明では正600胞体の正四面体を、アリシア胞の正二十面体に対応するものと、アリシア胞の正四面体に直接対応するものにグループ分けした。どうして、そのような苦しい説明になったかというと、正二十面体で表面を一回覆う四次元正多胞体が構成できないからである。しかし、「星形正多胞体」の項で述べたように、正二十面体が表面を4回覆う四次元立体{3, 5, 5/2}はある。こちらで説明できる可能性もあると思うのだが、将来への宿題としたい。
2002年9月23日 岡田好一