


 Statistical Analysis of Corrections on LoTT
Statistical Analysis of Corrections on LoTT




| 1. | Outline |
| 2. | Method |
| 3. | Result |
| 3a. | Double-Double Fit |
| 3b. | Solid Trumps |
| 3c. | Chameleons |
| 3d. | Notrump vs Singleton |
| 4. | Double-Fit Rule |
| 5. | Postscript |
Corrections (or adjustments) appear to be of utmost concern in the topic of LoTT (the Law of Total Tricks). In this article, results are quoted from the newest version of my freeware
The corrections have usually been discussed as to if they are justifiable. In the present statistical analysis, frequencies (probabilities) will also be studied for various types of extra factors (other than total trumps) that will require corrections.
| Extra Factors | Frequency |
| Double Double Fit | 12.0% |
| Double Solid Trumps | 8.5% |
| Nortrump vs Singleton | 47.3% |
For example, let me extract this table from the result below, where all three factors deserve a full +1 trick correction.
In this table, the first two lines refer to the suit-vs-suit contracts, while the bottom line to Notrump-vs-suit contracts.
When we speak of such and such corrections to LoTT, oddly enough, such and such cases will actually take place rather infrequently. Thus, if we take statistics over the whole ensemble of random deals, as has been initiated on a large scale by Matthew Ginsberg and extended by myself, such and such cases are smeared out, and we're unable to draw any conclusions on corrections from statistical analysis.
To avoid this, a new feature has been introduced into the above software, which will take statistics over only limited class of deals which satisfy such an such conditions.
At present, the software allows some 15 classes, the result from which are some clear and some unclear. The clearer ones will be mentioned below.
The software allows, in addition, to specify the range of HCPs. This restriction on HCPs will not be placed below, because the results have been found not to depend on HCPs, (although often claimed to the contrary without definite proof).
Furthermore, there remains a choice between the "Length Rule" and "Score Rule" on how to select trump suits. The former rule (chosen by Ginsberg, with Notrump calls totally ignored) takes automatically the longest suit as the trump, as if thinking it best, while the latter selects the trump suit (or Notrump) so that the net score be biggest for both sides, even in the presence of bitter competition and possible sacrifice bids.
In the analysis below, the latter is adopted, since it is more natural at bridge table. With this choice, there remain no ambiguities on selection of trump suits.
As usual, "Double Fit" is understood to mean 8 (+) cards in two suits in two hands. Let us begin with this class.
Is or isn't "Double Fit" a positive extra factor by itself?
| Owner | Probability |
| Both have | 12.0% |
| Only one side has | 24.2% |
| Neither has | 63.8% |
As a matter of fact, Jean René Vernes denies, and Larry Cohen emphatically denies. They agree on a positive correction only when the "Double Fit" is Double. That is to say, they count only when Both sides have a double fit.
We first ask how often a double-double fit will take place.
The answer is given in this table, and we know that a double-double fit occurs with probability 12.0%, surely infrequently, almost once in 8 deals, except Notrump-vs-Suit deals.
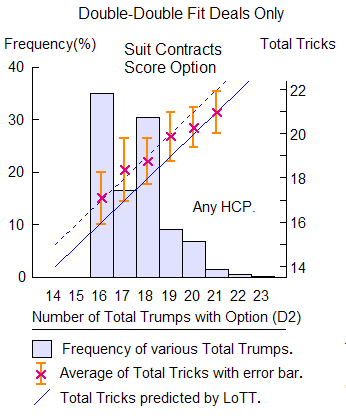
Next we restrict ourselves to the "double-double fit" class; we then obtain a figure like this, which consists of three parts:
- The bar graphs (in light blue, scale left) show the frequency of various total trumps. Here, total trumps 16 and 18 will both take place with high probability. The singular behavior of this frequency distribution will be separately explained below (actually, the above emphasis will turn out to be unnecessary).
- The red crosses (scale right) show averages of actual total tricks with the error bars.
Their length means that the average error is about 1 trick.
[When averaged over the total trumps, the deviation from the LoTT [A] turns out to be +0.92 tricks with an average error of 0.87 tricks.] - The blue solid line with inclination 45° represents the LoTT line
[A] Total Tricks = Total Trumps,whereas the dotted line[B] Total Tricks = Total Trumps + 1has been drawn for guide to eyes.
You may then ask what in case of a simple double fit (24.2%).
The result is as you may easily imagine: perhaps, +0.5 trick correction ? (click here).
Under this class, the software assumes the presence of A, K, and Q in the trump suit in combined hands.
Should this holding AKQ be Double, too?
| Owner | Probability |
| Both sides have | 8.5% |
| Only one side has | 36.0% |
| Neither side has | 55.5% |
This time, we hear no answers from both authors. They both claim importance of solid trumps, but neither clarifies if Simple solid trumps will be enough, or Double is necessary.
So, we try.
We start again to see how single/double solid trumps are likely. The table shows that Double solid trumps occur with a small probability 8.5%, again infrequently.
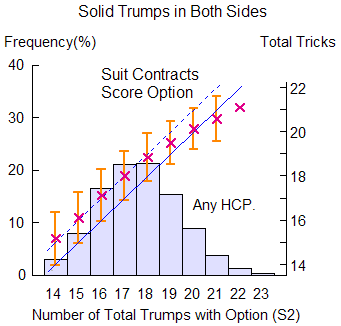
We then take statistics over these only 8.5% cases. The resulting figure is similar to the above double-fit case. Only with double-solid trumps, +1 trick correction is to be counted, up to 18 Total Trumps.
From 19 total trumps on, the tricks grow in less proportion to total trumps. This convex behavior of total tricks is a common feature: LoTT will tend to overestimate tricks for increasing trumps.
"Too many trumps" is a negative factor to LoTT (Just consider if you can hold down 2 losers, simply because you have 11 trumps).
You may then ask what in case of a simple solid trump. Perhaps you can easily imagine, but click here and see.
I love the short term "Chameleons" for minor honors in opponents' trump suit. They will sometimes win a trick in defense, but are useless in their own contract, just as chameleons behave differently under circumstances.
Even though there can be many kinds of chameleons, the software assumes, under this class, only the three-card holding Qxx, where x may include J and 10.
| Owner | Frequency | |
| (a) | Both have | 0.8% |
| (b) | Only one side has | 16.4% |
| (c) | Neither side has | 82.8% |
We have to note first how often chameleons will appear. The frequency values in the table were obtained from random 480 thousand deals (except Notrump deals).
So, we observe again that the phenomenon is infrequent.
In particular, it seldom appears in both sides together, and will never appear in 82.8% deals.
| Total Trumps | Both have | Only one side has | Neither has |
| 15 | 0.37±0.64 | 0.51±0.70 | 0.66±0.71 |
| 16 | 0.11±0.68 | 0.36±0.76 | 0.59±0.79 |
| 17 | 0.16±0.79 | 0.30±0.82 | 0.48±0.85 |
| 18 | 0.27±0.87 | 0.25±0.87 | 0.33±0.90 |
| 19 | 0.40±0.89 | 0.20±0.88 | 0.04±0.87 |
| 20 | 0.10±0.89 | −0.27±0.95 | |
| average | 0.25±0.73 | 0.37±0.78 | 0.44±0.82 |
Average tricks obtained in these three cases do not differ so much as to allow clear graphical comparison.
Hence, we show the result in this table:
Up to 18 total trumps, absence of chameleons is more a positive factor than its presence is a negative factor. Magnitude of correction is on the order of ¼ tricks.
Nevertheless, this favorable trend changes for larger total trumps for some reason unknown to me. Advantage of absent chameleons appears to be effective only for smaller total trumps.
Certainly, when a deal has lots of trumps and hence lots of tricks, other factors will dominate over presence/absence of chameleons.
We next consider deals where one side is playing Notrump. Correction (or adjustment, or LoTT formula itself) proposed by Jean-René Vernes reads
[V] Total Tricks = Number of Trumps + 8, 7, 6,
where the three numbers on the right correspond to a void, singleton and doubleton
in a side suit of opponents.
As to the owner of this void/singleton, we follow Jean-René Vernes to count a void/singleton in (supposed) dummy as well as in (supposed) declarer.
We have also Larry Cohen's version in To Bid or Not To Bid:
[C] Total Tricks = Number of Trumps + 8, 7½, 7.
| Shape | Frequency |
| Void | 9.6% |
| Singleton | 47.3% |
| Doubleton | 43.1% |
Let us begin with relative frequency of a void, singleton, and doubleton.
The table on the right has been obtained from 236 thousand random deals (except suit-suit contracts).
Please notice that this frequency distribution is appropriate only when one side is going to play Notrump. Rather flat hands of Notrumpers will tend to make the opponents' hands also flat.

As a result, voids will appear more infrequently, but singletons remain still fre-quent.
We now ask
In this graph, two lines are drawn for guide to eyes, the solid line for Number of trumps + 7, and the broken line for Number of trumps + 8.
This graph clearly shows that, in the "Notrump vs Singleton" class, neither [V] nor [C] works better than the proposed Singleton formula,
[S] Total Tricks = Number of Trumps + 8 (for singletons).
You may ask what if opponents have only doubletons,
just click here. You'll find for yourself a Notrump formula
for doubletons.
As for voids, the tricks heavily depend on the number of trumps, and we're unable to draw such a simple formula for voids. The tricks available will depend more on bidding situa-tions, e.g., whether you're overcalling against NT opening in the direct position or in the balancing position.

In this paragraph, we look back to our first figure (reproduced on the right) and consider the origin of its singular distribution.
To set up a handy notation, let [8d] denote 8+8 double fits (8 cards in two suits), and let [9d] denote 9+8 as well as 9+9 double fits.
These two kinds of double fits will take place in 10.34% and 7.88% deals, respec-tively. We've discussed this kind of probability elsewhere(Sec.6) in depth, but we will repeat in the present context.
Now, it is obvious that the double peaks at 16 and 18 trumps arise, respectively, from the [8d]+[8d] double-double fits and the [9d]+[9d] double-double fits. In this connection, it is interesting to note that the [8d] and [9d] double fits can never coexist.
| Our Shape | Their Shape | Double Fit | Frequency | |
| (a) | [8,8,8,2] | [5,5,5,11] | none | × 1.3% |
| (b) | [8,8,7,3] | [5,5,6,10] | none | ×19.0% |
| (c) | [8,8,6,4] | [5,5,7,9] | none | ×47.6% |
| (d) | [8,8,5,5] | [5,5,8,8] | * | ×32.1% |
To put the other way, suppose your side have an [8d] double fit, they (opponents) can then certainly have an [8d] double fit, but never can they have a [9d] double fit. This is an aspect of the "Double-Fit Rule", which may be proved plainly:
When you have an [8d] double fit, your shape should be one of (a) − (d) listed in the table, and correspondingly, opponents will have the complementary shape of 13.
Their possible double fit is hence limited to only [8d] realized in the case (d). Their double fit can never be [9d].
| ||||||||||||||||||||||||||||||
|
Its extension to the 9+8 double fit is straightforward:
If you have a 9+8 double fit, their double fit is limited also to a 9+8 double fit, (again the bottom case (d) in the list).
In case (though very unlikely) we have a 9+9 double fit, they can have two kinds of double fits (d) and (e), which can never be 9+8 nor 8+8. Q.E.D.
Thus, we have shown that the three double fits 8+8, 9+8, and 9+9 have no intersections each other.
We note in passing that your [9d] has more chance (than 32.1% in [8d]) for opponents to have a double fit, too. This fact is perhaps, at least qualitatively, known to many bridge players.
The table below shows quantitatively that, the more shapely hands you two have got, the more shapely hands opponents are likely to have. The difference between the [8d] and [9d] double fits is really great.
| Your Shape | Double Fit | Double Double Fit |
| 8d | 10.34% | ×32.11% |
| 98 | 6.92% | ×59.25% |
| 99 | 0.97% | ×79.84% |
| 10d | 1.74% | ×82.53% |
| 11d | 0.20% | ×93.77% |
From this double-fit rule, we easily understand why the distribution is strongly peaked at 8+8=16 and 9+9=18 trumps.
It's OK for 16 and 18, but what about 17 trumps? If the [8d] and [9d] double fits really never coexist, frequency of the 17 trumps should be strictly zero.
Why is it non-vanishing at 17 trumps in that graph ?
Actually, there is no contradiction.
If we select automatically the longest suit as the trump suit, then entry in the 17 trumps will be strictly zero, indeed. But, bridge bidding is not so simple.
Suppose that you have a 9+8 double fit, which consists of 4-4 cards in
 and 5-4 in
and 5-4 in  ,
while opponents are most likely (59.3%) to have also a 9+8 double fit, 5+4 in
,
while opponents are most likely (59.3%) to have also a 9+8 double fit, 5+4 in  and 4+4 in
and 4+4 in  .
Against their 3
.
Against their 3 bid, you'll compete with 3
bid, you'll compete with 3 , with shorter
, with shorter  than
than  .
As a result, total trumps will become 8 (your
.
As a result, total trumps will become 8 (your  ) + 9 (their
) + 9 (their  ) = 17.
) = 17.
The double-fit rule is very useful at bridge table. Owing to this rule, you don't need to worry about if the deal is double-double or single-double.
The logic is easy:
When you have an [8d] fit, the double-fit rule will guarantee that opponents will have at least an [8d] fit. In that case (32.1%), you can expect
8 + 8 + 1 correction = 17 total tricks,
because of the double-double fit;
or else they have at least 9+7 shape (47.6%) or more, and hence
8 + 9 = 17 tricks (from the LoTT formula).
In either case, you can expect 17 tricks. Therefore, it is unnecessary to
emphasize double-double fit. The deal is effectively
double-double, once you have a double fit. So, it suffices to say simply
double fit.
We have so far examined various possible corrections to LoTT, together with the probabilities with which they take place. We have found most of them are rather infrequent.
| Extra Factors for Corrections | Frequency |
| Double Double Fit | 12.0% |
| Double Solid Trumps | 8.5% |
| Nortrump vs Singleton | 47.3% |
So, it is not clever, particularly for beginners, to be overly sensitive to these corrections. An important exception is the "Notrump vs Singleton" case, which will occur with probability 47.3%, and the above statistical analysis strongly suggests the proposed LoTT formula [S] for that case.
In case you're anxious about detailed corrections on LoTT, the
earlier remark (p.40)
by Jean-René Vernes is to be remembered. He compares results
of all the deals in 1953-1959 world championships, which were played in
two rooms with the same trump, on the same level, and played by the
same side. The number of tricks taken varied ±0.52 tricks, even
among this level of players;
from which [regarding it as an unavoidable error,] he concludes that a formula which could predict the number of total
tricks with an accuracy of a half trick may be considered as rigorously perfect.