はんすのWebSite
|
冷却曲線から熱伝達係数を求める (1/1ページ) |
ここでは、最小二乗法をもちいて物体の冷却曲線から熱伝達係数を求める方法について述べています。
熱伝導方程式を立てる
ここでは、真空チャックのうえに密着して置かれている樹脂製基板を考え、基板からチャックへの熱伝達係数α(SI単位はW/(m2℃))を求める実験を例として挙げます。基板表面がレーザーによりある一定温度T0(単位℃)にまで加熱、保持されます。時刻t=0(単位s)にレーザーをオフした後の基板Ts(単位℃)の冷却温度曲線を熱電対で測定します。厚みd(単位m)の基板は薄いので基板内で温度分布は無く、一様であるであるとします。真空チャックは水冷されており、かつ基板よりも熱容量が大きいのでレーザーオフ後の温度変化は無く、常にTc(単位℃)であるとします。基板の定積比熱をCv(単位J/m3℃)とすると、基板冷却時の基板全体の熱伝導方程式は次のようになります。

![]()
ここで左辺は基板温度の変化を、右辺は基板からチャックへの熱流速(単位W/m2)を表しています。この微分方程式をTsについて解くと、2つの境界条件、t=0のときTs=T0、およびt=∞のときTs=Tcより、
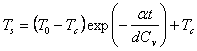
が得られます。
最小二乗法を用いて測定した冷却曲線を理論式にフィッティングする
先ほどの式において、T0はt=0のときの温度を読み取ることで得られ、dとCvは材料の形状と材質から既知です。またtの変化に伴うTsの変化も測定しています。よって未知なのはTcとαです。ここでは、最小二乗法を用いて測定データを理論式にフィッティングさせることによって、この2つの未知定数を求めます。
T0=113℃、d=0.0004m、Cv=2.1E+6J/m3℃とし、基板温度Tsをy、時刻tをxとします。また、Tcをk0、αをk1とすると先ほどの式は次のように記述できます。
y=(113-k0)*exp(-k1*x/(0.0004*2.1E+6))+k0
最小二乗フィッティングソフトウェアRSquareの計算条件にこの式を入れ、さらにtの変化に伴うTsの変化の測定データを開いてフィッティングさせると、次のようにチャック温度Tc=k0=26℃、熱伝達係数α=k1=86W/(m2℃)が得られます。
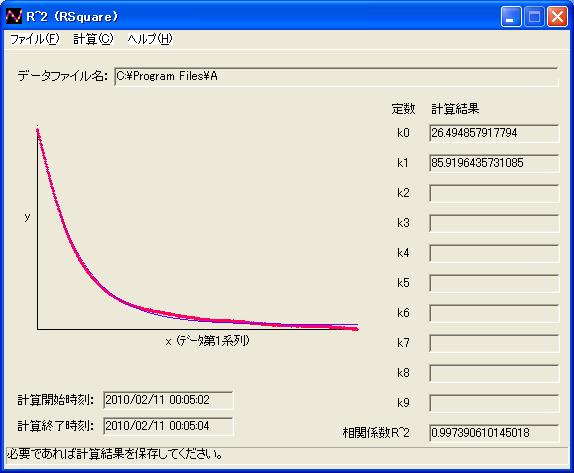
|
|
| トップページへ戻る |
はんすのWebSite