�͂�WebSite
|
�͂�WebSite |
�ŏ����@�Ȃǂ̌v�Z�@���g�������w�I��@����g���čH�w��̖����������Ƃ̖ʔ����ɂǂ��Ղ�Ђ����Ă��܂����G���W�j�A���A�Ȏq���Q�����Ƃ̏T���̐[��̎��Ԃ��g���č쐬���Ă���y�[�W�ł��B
���̃y�[�W�ł́A�ŏ����@�i�ŏ�����@�Ƃ������A�p��ł�Least
Squares Method�j���g���Ă��܂��܂Ȗ��������Ă����܂��B�ŏ����@�Ƃ́A�ߎ��Ȑ��i�t�B�b�e�B���O�J�[�u�j�����߂鐔�w�I��@�ł��B���̕��@�͂��낢��ȏ�ʂŔ��ɖ𗧂��܂��B�����f�[�^�𗝘_�Ȑ��Ƀt�B�b�e�B���O������A�������猩���Ă�����̂����낢�날��܂��B
|
�ŏ����@�Ƃ� |
�ǂ������Ƃ��ɍŏ����@���g���̂��H
�����Ȃǂœ���ꂽ�����̃f�[�^�_���O���t��Ƀv���b�g�������ƁA�����̓_�Ƀt�B�b�g����ߎ��Ȑ��i�t�B�b�e�B���O�J�[�u�j�����Ƃ����ꍇ������܂��B�Ⴆ�A
1.
�f�[�^�_�Ƀt�B�b�g���钼���̌X�������߂����Ƃ�
2.
���K���z�i�K�E�X���z�j���Ă��镨���ʕ��z�̓��v�ʁi���ϒl�A�W�����Ȃǁj�����߂����Ƃ��i�K�E�X�t�B�b�e�B���O�j�B
3.
�����̃s�[�N���d�Ȃ��Ă���X�y�N�g���̔g�`�����i�s�[�N�����j���������Ƃ�
�����ȊO�ɂ��F�X�ȏꍇ������܂��B�v���b�g���ꂽ�f�[�^�𗝘_���Ƀt�B�b�e�B���O�����邱�Ƃɂ���āA���_�����Ɋ܂܂��萔��������ł��邩��m�邱�Ƃ��ł��A�������炳�܂��܂ȏ��邱�Ƃ��ł��܂��B���̍ہA�ŏ����@�̓t�B�b�e�B���O�Ɍ������Ȃ���@�ƂȂ�܂��B
��̗�i�d���̎��ԕω������R�A�Ód�e�ʂ����߂�j
�����ł́A������������ꂽ�f�[�^�_���A�ŏ����@��p���ė��_���Ƀt�B�b�e�B���O�����邱�Ƃɂ���R�A�Ód�e�ʂ����߂��������܂��B
�ڍׂȐ������Ȃ��܂����A���}�̂悤�Ȓ����d���A��R�A�R���f���T�̒���ڑ�����Ȃ�d�C��H�Ɏ���t=0�ɃX�C�b�`��ON�����ꍇ�A�����d��I (t)��I=(V/R)exp(-t/CR)�ƕ\����܂��B
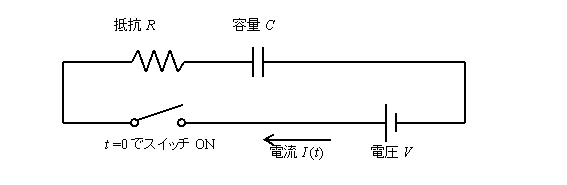
�����ŁA�d��V�͊��m�ł���A��RR�Ɨe��C�����m�ł����āA�������������ʂ��狁�߂邱�Ƃ��l���܂��B�d���̎��ԕω��������ő��肵�A���̐}�̂悤�Ȍ��ʂ�����ꂽ�Ƃ��܂��B
��قǂ̗��_������R��C�ɓK���Ȓl����荞��œd���̎��ԕω��̃O���t��
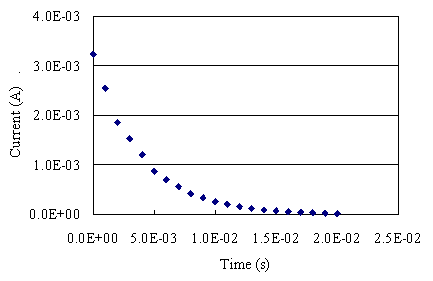
�`���ƁAR��C�̒l�̈Ⴂ�ɂ���Ă��܂��܂ȃJ�[�u��`�����Ƃ��ł��܂��B���̂��Ƃ�\�����̂��A����2�̐}�ł��B
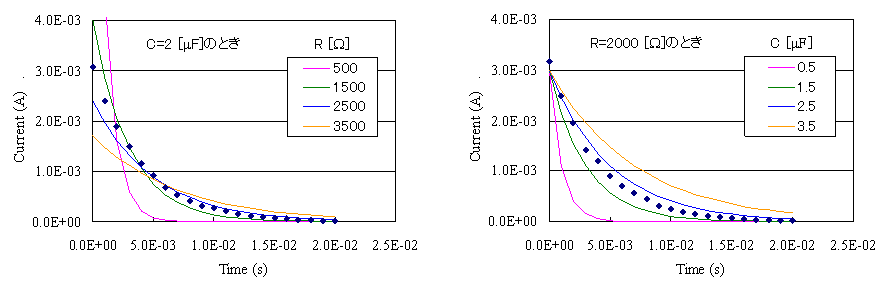
�����������̒��ł��A�K��R��C�̒l��p���ăO���t��`���A�������ʂƈ�v����J�[�u��������͂��ł��BR��C�̒l�����߂�Ƃ�����Ƃ́A�������ʂ̋Ȑ��ƈ�v����R��C�̒l��T���o���Ƃ�����ƂƓ����ł��B�����Ńt�B�b�e�B���O�̎�@�ł���ŏ����@�̏o�ԂƂȂ�܂��B
�@�@�����œ���ꂽ�J�[�u���A�ŏ����@��p���ė��_���Ƀt�B�b�e�B���O������ƁA���}�̂悤�ȃt�B�b�e�B���O���ʂ���ƂƂ��ɁA���m��R��C��m�邱�Ƃ��ł��܂��B
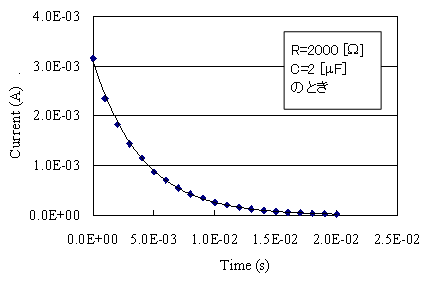
�ŏ����@�̐��w�I����
�ŏ����@�i�ŏ�����@�j�͋ߎ��Ȑ��i�t�B�b�e�B���O�J�[�u�j��ۂɁA�����Ƃ��悭�g���鐔�w�I��@�ł��B�ȉ��ɁA���w�I���������܂��B�����ł͊ȒP�̂��߂�1�̃f�[�^�_��2�̕����ʂ���\���������̂Ƃ��܂����A3�ȏ�̏ꍇ���������l�����܂��B
n�̃f�[�^�_��(x1, y1), (x2,
y2), ���,
(xn,
yn)�Ƃ��A�����f�[�^�_���t�B�b�g�����y = f (x)��������ꍇ���l���܂��B�ŏ����@�ł͂��̖��O�̒ʂ�A
![]()
���ŏ��ɂȂ�悤��y = f (x)�����߂���@�ł��B�����ŁAf
(x)�̒��Ɋ܂܂�Ă���萔��k�P, k2, ���,
km�Ƃ���ƁAS���ŏ��ɂȂ�悤��k�P, k2,
���,
km��T���o���Ƃ������ƂƓ����ł��B�Ⴆ�A�ꎟ��y =k1 x�{k2�Ƀt�B�b�e�B���O���������ꍇ�ɂ́A
![]()
�ɂ�����S���ŏ��ɂȂ�悤��k1 ��k2�����߂邱�ƂɂȂ�܂��B
S���ŏ��ɂȂ�̂͋ɏ��l�����Ƃ��ł��̂ŁA�X����0�ł��邱�Ƃ���A1����m�܂ł̂��ׂĂ̐���j�Ɋւ��Ď��̎������藧���܂��B
![]()
����@
�����ŁA
![]()
����A
�Ƃ����ƍ��ӂ́A

�ƂȂ�܂��Byi�͒萔�ł��邱�Ƃ���kj�ł̕Δ�����0�ł���A����Ɍv�Z��i�߂�ƁA
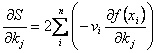
�ƂȂ�܂��B����ć@�����A
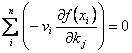
�������A����ɇA����������ƍŏI�I�Ɏ��̎��������܂��B
![]()
1����m�܂ł̂��ׂĂ̐���j�Ɋւ��Ă��������S���ŏ��ɂȂ�悤��k�P, k2, ���,
km�����߂�ꂽ���ƂɂȂ�܂��B
�t�B�b�e�B���O�ɂ͌v�Z�\�t�g�E�F�A���g���̂���ʓI
���̂悤�Ȍv�Z�͏ꍇ�ɂ���Ă͔��ɔώG�ł����A����ɂ͉�͓I�ɂ͉������߂邱�Ƃ��ł��Ȃ��ꍇ������A��v�Z�ōs�����Ƃ͂��܂茻���I�ł͂���܂���B�����ŁA���ԂƎ�Ԃ��Ȃ����߂ɁA�ŏ����v�Z���s���Ă����\�t�g�E�F�A�𗘗p���邱�ƂɂȂ�܂��B
�t�B�b�e�B���O�v�Z���������\�t�g�E�F�A
�����ł́A���ɔώG�ȍŏ�����v�Z���ȒP�ɍs���Ă����\�t�g�E�F�A�ɂ��ďЉ�܂��B
�����ŏЉ��RSquare�͍ŏ����v�Z��p���A���肳�ꂽ�f�[�^�Ƀt�B�b�e�B���O����ߎ��Ȑ������߂Ă����\�t�g�E�F�A�ŁA���̂悤�ȓ���������܂��B
1.
���`�������łȂ��A�w���A�ΐ��A�O�p���A�t�O�p���A����ɂ�����g�ݍ��킹�����ւ̃t�B�b�e�B���O���\�ł��B
2.
���������āA���K���z�i�K�E�X���z�j�ւ̃t�B�b�e�B���O���\�ł���A����ɐ��K���z�̕����s�[�N���d�˂��킳�ꂽ��Ԃ�g�`�����i�s�[�N�����j���邱�Ƃ��\�ł��B
3.
�t�B�b�e�B���O�̌��ʂ��ȈՃO���t��Ŋm�F���邱�Ƃ��ł��邤���A���̃f�[�^�ƃt�B�b�e�B���O���̑��ւ̋�����\���w���ł��鑊�W��R^2�����邱�Ƃ��ł��܂��B
4.
��ʍʼn����ɕ\�������X�e�[�^�X�o�[�̎w���ɏ]���đ����i�߂Ă䂭�����ŁA�ȒP�Ƀt�B�b�e�B���O���ʂ邱�Ƃ��ł��܂��B
5.
�T���v���t�@�C�������Ă���A�K�E�X�t�B�b�e�B���O��g�`�����̕��@��̌����邱�Ƃ��ł��܂��B
�g�����̐��������������ǂ����B
�\�t�g�E�F�A�̃_�E�����[�h
���̃{�^�����N���b�N�����Vector�̃T�C�g����\�t�g�E�F�A���_�E�����[�h���邱�Ƃ��ł���T�C�g�փW�����v���܂��B
|
�ŏ����@�̗��p�� |
�ŏ����@���g���čH�w��̖�����͂���������Љ�܂��B�i�ꕔ�A�ŏ����@�Ƃ͊W�Ȃ����̂��܂܂�Ă��܂��B�j
���₳�ꂽ���̏�ɒu����Ă�����M���ꂽ���̗̂�p�Ȑ�����A2�̕��̊Ԃ̔M�`�B�W�������߂܂��B
��R�E�R���f���T�E�R�C���̒���ڑ��ɒ����d������������ꍇ
���w�I�ɋ�������͂������ʂ�������܂��B�������������ꍇ�������Ȃ�������ƁA�ʔ������ʂ������܂��B
�H�w��Ŗ��ɗ������N���f�ڂ��Ă��܂��B
|
|
�͂�WebSite