�͂�WebSite
|
��R�E�R���f���T��R�C���̒���ڑ��ɒ����d������������ꍇ �i1/2�y�[�W�j |
�����ł́A�������������������Ƃɂ��A��R��R���f���T�E�R�C���̒���ڑ��ɒ����d������������ꍇ�̋�������͂��܂��B
�d���̎��ԕω����v�Z����
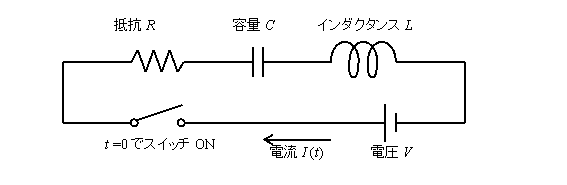
��̐}�̂悤�ȉ�H���\�������ꍇ�̓d���̎��ԕω����v�Z���邱�Ƃ��l���܂��B����t =0�ŃX�C�b�`��ON�����ꍇ�A��H�ɗ����d��I
(t)�͂ǂ�Ȏ��ԕω�������ł��傤���B
���̖����������߂ɂ́A��R�A�R���f���T�A�R�C���̂��ꂼ��̗��[�ԂŔ�������d���~�����d���d���ɓ������Ƃ������Ƃ𗘗p���܂��B���Ȃ킿�A����t�̂Ƃ��ɃR���f���T�ɗ��܂��Ă���d�ׂ�Q(t)�Ƃ��āA
![]()
�ƂȂ�܂��B�����Q(t)�́A
![]()
�ł��̂ōŏI�I�ɁA
![]()
�������܂��B����I
(t)�Ɋւ��������������������A��H�ɗ����d���̎��ԕω���m�邱�Ƃ��ł��܂��B
����������������
�@����t�Ŕ�������ƁA
![]()
�������܂��BI (t)=Aexp(g t)�Ƃ����ƁA�A����莟�̓����������������܂��B
![]()
����������āA
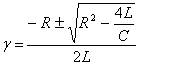
�������܂��B���������āA���̔����������̉��́A�������̒������ł��邩���ł��邩�ɂ���Ď��̃y�[�W�̂悤�ɏꍇ�����ł��܂��B�i�����ɂ͕������̒����[���̏ꍇ�����݂��܂����A�����ł͊������܂��B�j
�b�@�g�b�v�y�[�W�֖߂��@�b
�͂�WebSite