�͂�WebSite
|
��R�E�R���f���T��R�C���̒���ڑ��ɒ����d������������ꍇ �i1/2�y�[�W�j |
�����ł́A��قǂ̔������������������Ƃɂ��A��R��R���f���T�E�R�C���̒���ڑ��ɒ����d������������ꍇ�̋�������͂��܂��B
(1) R�Q���SL/C�̏ꍇ
���̏ꍇ�A�������̒��͐��ƂȂ�܂��B������������2�̉������ꂼ��

�Ƃ����ƁAI (t)�͎��̂悤��2�̉��̐��`�����ŕ\����邱�ƂɂȂ�܂��B
![]()
�����ŁA����t =0�̂Ƃ��ɂ͗����d��I (t)=0�ł���̂ŇB�����A2=�|A1�ƂȂ�܂��B����āA
![]()
�������܂��B���������t =0�̂Ƃ��ɂ̓R���f���T�ɂ͓d�ׂ����܂��Ă��Ȃ��̂ŁA
![]()
�ł��B�C�D�����@���ɑ������t=0�̂Ƃ��ɂ��čl�����A1�����̂悤�ɋ��߂��܂��B

������C���ɑ�����Đ�������ƍŏI�I��I (t)�����߂��܂��B

����̃O���t��`���Ɖ��̂悤�ɂȂ�܂��B
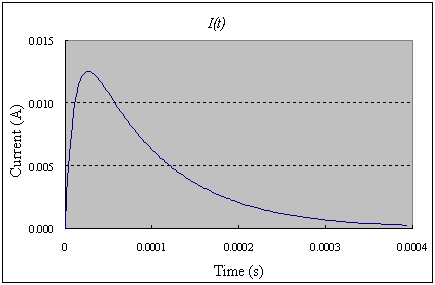
V=15[V]�AL=10[mH]�AC=0.1[mF]�AR=1[kW]�̂Ƃ��̐��l�v�Z���ʂł��B�d���͈�U�㏸�����̂��A��������Ƃ����ߒ������ǂ�܂��B
(2) R�Q���SL/C�̏ꍇ
���̏ꍇ�A�������̒��͕��ƂȂ�܂��B������������2�̉������ꂼ��
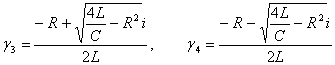
�Ƃ����ƁAI (t)�͎��̂悤��2�̉��̐��`�����ŕ\����邱�ƂɂȂ�܂��B
![]()
�����ŁA����t =0�̂Ƃ��ɂ͗����d��I (t)=0�ł���̂ŇF�����A3=�|A4�ƂȂ�܂��B����āA
![]()
�������܂��B���������t =0�̂Ƃ��ɂ̓R���f���T�ɂ͓d�ׂ����܂��Ă��Ȃ��̂ŇD�������藧���܂��B
�D�G�����@���ɑ������t=0�̂Ƃ��ɂ��čl�����A3�����̂悤�ɋ��߂��܂��B
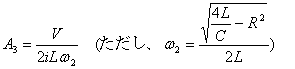
������G���ɑ�����Đ�������ƁA

����̎����������Ƃ�ƍŏI�I��I (t)�����߂��܂��B
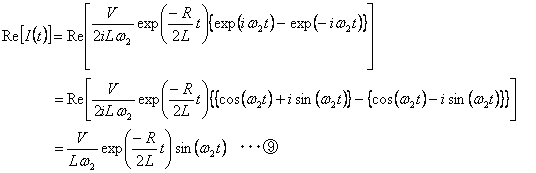
����̃O���t��`���Ɖ��̂悤�ɂȂ�܂��B
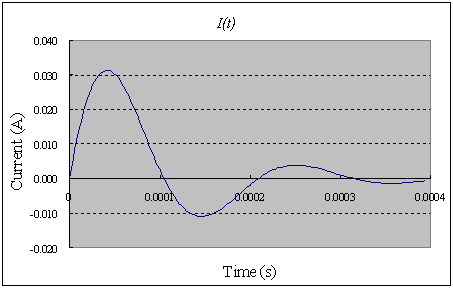
V=15[V]�AL=10[mH]�AC=0.1[mF]�AR=1[kW]�̂Ƃ��̐��l�v�Z���ʂł��B�d���͐U�����Ȃ��猸������Ƃ����ߒ������ǂ�܂��B
�b�@�g�b�v�y�[�W�֖߂��@�b
�͂�WebSite