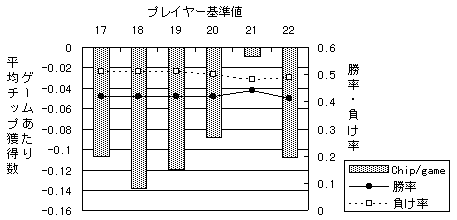
図1 : バリュー中央値利用タイプの対戦成績
5,000ゲームからなる予備試行の結果である。各αタイププレイヤーは、現在のカード合計と次に引きうるカードの中央値との合計を計算し、それが基準値以下であるかぎりヒットする。勝率、負け率は、プレイヤーとディーラーがいずれもブラックジャックでなかったゲームに限ってのデータをとった。
最終的に、基準値を21とするプレイヤーが獲得チップ数・勝率・負け率のいずれにおいても、最良の成績を収めた。
以下の三タイプを設定した。α、β、γの順に能力は劣ってくる。
以下の三種の推論を設定する。A,B,Cの順に情報処理に柔軟性が加わる、つまり推論が精緻になると考えてよいだろう。
各推論について、上記α、β、γの三タイプのプレイヤーをおのおの配する。 つまり合計で9種類の戦略プレイヤーを設定した。
以下で戦略A、B、Cの詳説を行なう。
この型のプレイヤーは、次に引きうるバリューの中央値(つまりシューの残りカードの中央値)を計算し、それと現在のカード合計との和が一定の基準値以下である限りヒットを続ける。例えば基準値を21に設定すれば、そのふるまいは「バストする確率が1/2を超えるまでヒットを続ける」と換言できる。
この基準値は、一見したところ21が最もふさわしいように思われる。ただしカード合計が22以上になればプレイヤーは無条件で負けになる以上、やや低めに設定した方が良いようにも思われる。ここでは最適な基準値を求めるため、予備試行として17,18,19,20,21,22の各基準値をとるαタイププレイヤー6人をディーラーと共に5,000ゲーム戦わせ、対戦成績を見た。結果は以下のようになった。

図1 : バリュー中央値利用タイプの対戦成績
5,000ゲームからなる予備試行の結果である。各αタイププレイヤーは、現在のカード合計と次に引きうるカードの中央値との合計を計算し、それが基準値以下であるかぎりヒットする。勝率、負け率は、プレイヤーとディーラーがいずれもブラックジャックでなかったゲームに限ってのデータをとった。
最終的に、基準値を21とするプレイヤーが獲得チップ数・勝率・負け率のいずれにおいても、最良の成績を収めた。
以上の結果より、αタイププレイヤー(Aα)のとる最適な基準値を21とする。つまりAαプレイヤーは、現在のカード合計と、残りカードの中央値の和が 21 以下である限りヒットする。
βタイププレイヤー(Aβ)についても同様に予備試行を行い、最適基準値20を得た。
γタイププレイヤー(Aγ)は、1デック全体のカード中央値が約 6.54なので、「14以下なら一律にヒット、15以上なら一律にステイ」という戦略をとることになる。
このタイプのプレイヤーは、カード合計から期待される経験的な配当額を参照する。そしてヒットする場合/ステイする場合各々での配当期待値を計算・比較し、より高い値のオプションを選択する。
プレイヤーは、自分のカード合計が12以上20以下の場合、ヒット/ステイそれぞれでの配当期待値を比較することになる。ただし、もし一枚ヒットしたあとの合計がまだ20以下だったなら、さらにその時点でのヒット/ステイそれぞれの配当期待値の比較も必要になる。(場合によっては、二枚ヒットした方が配当期待値が高くなるため。)
つまり、現在のカード合計値をにらみつつプレイヤーが行なうべき計算は
I : 今のままステイしたときの配当期待値 Es
II - (1) : 一枚ヒットしたときの配当期待値 Eh1
III - (2) : 二枚ヒットしたときの配当期待値 Eh2
の三つとなる。(三枚以上ヒットした時の配当期待値はあえて無視する。)
II の (1) と (2) を比較して高い方をII全体の値Ehとし、その上でEsとEhを比較する。
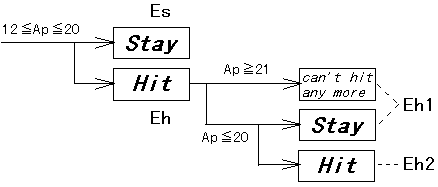
図2 : プレイヤーのカード合計と選択肢
図中のApは、プレイヤーのその時点でのカード合計を示す。
プレイヤーはカード合計が12以上20以下の場合、まずその時点でステイする場合の配当期待値Esと、ヒットする場合の配当期待値Ehを計算する。ただし、一枚ヒットした時点でまだ合計が20以下の場合はまだヒットする可能性があるので、ヒットを一枚で止めた場合の配当期待値Eh1と二枚ヒットした場合の配当期待値Eh2をまず別々に計算し、高い値の方をEhとして採用する。それからEsとEhを比較し、より高い値のオプションを選択する。
なお、二枚ヒットした時点でなおまだ合計が20以下の場合、さらにEh3以下が計算できる。しかし筆者が試算したところ12≦Ap≦20である限り、常にEh3はEh1、Eh2の両方を下回った。(つまり値が採用される可能性はない。)Eh4以下も同様である。したがってこのケースではEh3以下を無視する。
まず、10000ゲームからなる予備試行で得られたデータより、最終的なカード合計ごとの配当の平均値を求めたところ、以下の表1の結果を得た。
| カード合計 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22〜 |
|---|---|---|---|---|---|---|---|---|---|---|
| 平均配当 | -0.84 | -0.82 | -0.75 | -0.80 | -0.39 | 0.11 | 0.71 | 1.25 | 1.87 | -2.00 |
10,000ゲーム中プレイヤー・ディーラー共にブラックジャックでなかった場合に限り、6人のプレイヤーの最終的カード合計とその時の配当を記録・集計し、それをもとに最終的カード合計から期待される配当を計算した。最終的カード合計が17以上になると、ほぼ直線的に期待される配当が伸びることがわかる。なお、最終的カード合計が21の場合でも期待される配当が2にならないのは、ディーラーと同着で追加配当が得られないケースのためである。カード合計が12以下のデータは得られなかった。
この表1の値をもとに、図2のEs、Eh1、Eh2が以下のように計算できる。
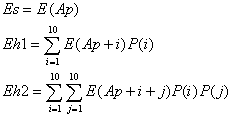
Ap : プレイヤーの現在のカード合計
P(i) : 次にiのバリューを引く確率
E(a) : カード合計aから期待される配当(表1による)
Eh2においては、 Ap+i < 21 が条件
プレイヤーは以上の式1〜3の結果、Es≧Eh1かつEs≧Eh2であればステイが有利と判断し、 Es<Eh1あるいはEs<Eh2ならばヒットが有利と判断することになる。
なおこのプレイヤーの一般的ふるまいを見やすくするため、便宜的にシューに丸々1デック残っている場合にBαプレイヤーが計算する配当期待値をプロットしてみた。
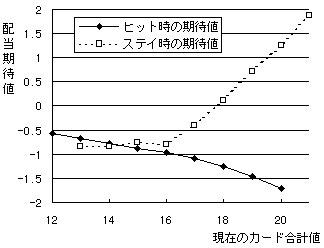
図3:各カード合計時に、ヒット/ステイすることによる配当の期待値。 (Bαプレイヤーの計算)
一般的傾向を見るため、便宜的にシューに丸々1デック残っているものと仮定している。(無論、現実には無いケースである。)ステイ時の期待値は先の表1の値を用い、ヒット時の期待値もそれを元に計算している。( 12 でステイした場合のデータは得られなかった。また 21 の時にはもうヒットできない。)
この場合、Bαプレイヤーは手持ちのカード合計値が14以下のときはヒットし、15以上の時はステイするであろう。
グラフではカード合計値が14から16の時ちょうど谷間になっており、ここがヒットするのもステイするのも難しい、いわゆる「危険地帯」であることを示している。
Bγプレイヤーは、図3の結果を一律に採用する。つまり「14以下のときはヒットし、15以上の時はステイ」となり、結果的にAγプレイヤーと全く同じふるまいをすることになる。
次へ(C型推論 : アップカード利用型)
(C) 1996 Nakamura Masaaki