前へ

Ｃ型推論 ： アップカード利用型

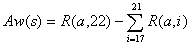
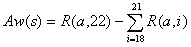
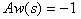
　ディーラーが唯一公開するアップカードは、彼の手の内を読む重要な手がかりといえる。 このタイプのプレイヤーは、ディーラーのアップカードから経験的データに基づき彼の手を評価し、ヒット時／ステイ時の各々について総合評価を行なう。

　まず予備試行の結果、ディーラーのアップカードとその最終的なカード合計との対応は、以下のようになった。

　10,000ゲームからなる予備試行の結果である。表側がディーラーのアップカードのバリュー（エースは一律１の行にまとめた）、表頭がそのゲームにおけるディーラーの最終的なカード合計を示している。
　アップカードのバリューが2以上６以下の時、ディーラーが際立ってバストする割合の高いことがわかる。またエースのバストする割合の低さ、ブラックジャックになる割合の高さも目を引くところである。

　プレイヤーは以下の表３に基づいて、ディーラーの手の評価を行なう。（プログラム実行時の負荷を減らすため、表２を簡略化したものである。）

　表側がディーラーのアップカードのバリュー、表頭がディーラーの最終的なカード合計を示している。プレイヤーはディーラーのアップカードを見て、（ブラックジャックでない限り）この表にある確率でディーラーの最終的なカード合計が定まると考える。

　例えばディーラーのアップカードが２、プレイヤーのカード合計が19だったとする。ディーラーの最終的なカード合計が未だ分からないとしても、上の表より勝負の見込みを計算できる。すなわちディーラーが17,18,バストだった時はプレイヤーの勝ち。19だった時は引き分け。20,21ならディーラー側の勝ちである。それらの見込みは、表であてはまる各値を合計することで求められる。順に、勝てる見込みは0.64(= 0.12 + 0.12 + 0.40)、引き分けの見込みは 0.12、負ける見込みは 0.24(= 0.12 + 0.12)となり、この条件ではかなり高い見込みで勝つことがわかる。
　このアップカード利用型プレイヤーは、総合評価として勝てる見込みと負ける見込みとの差を用いる。（引き分けの見込みも考慮に入れるため。）すなわちこの場合ならば0.64 - 0.24 = 0.40がその総合評価にあたる。

　まず以下の定義を行なう。

• Aw(s) : プレイヤーの最終的なカード合計が s の時、ディーラーに勝てる見込み。(0≦Aw(s)≦1)
• Ad(s) : プレイヤーの最終的なカード合計が s の時、ディーラーに負ける見込み。(0≦Ad(s)≦1)
• A(s) : プレイヤーのカード合計sの総合評価。A(s) = Aw(s)-Ad(s) で求められる。(-1≦A(s)≦1)
• R(t,u) : ディーラーのアップカードが t の時に、ディーラーの最終的なカード合計が u になる見込み。表３の数値をそのままあてはめる。ディーラーがバストした場合は、一律に合計を 22 とする。

アップカードのバリューが a の時、Aw(s) は以下のようにして求められる。

● s < 17 の場合 ：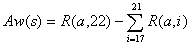
● s = 17 の場合 ：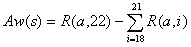
● 17 < s < 21 の場合 ：
● s = 21 の場合 ：
● 21 < s の場合 ：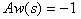

　Ad(s)についても同様の計算が行なえ、こうして A(s) が計算できる。そしてこれより、まず現在のカード合計 s でステイした場合の総合評価 As(s) が行なえる。

　次に、プレイヤーがカード合計 s からさらに一枚ヒットした場合を考える。　i のバリューのカードを引く確率を P(i) とすると、ヒット後に勝てる見込み Awh1(s) は以下のように求められる。

( s < 21 )

　一枚ヒット後、s+i < 21 だった場合は、さらにもう一枚ヒットできる。こうして二枚目をヒットしたあと勝てる見込み Awh2(s) は以下のように求められる。

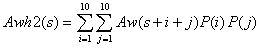
( s + i < 21 )

　同様にして、ヒットした場合に負ける見込み Adh1(s), Adh2(s) が各々計算され、総合評価 Ah1(s), Ah2(s) も求められる。

　プレイヤーは Ah1(s) と Ah2(s) のいずれを採用するか、（一枚ヒットし終った時点で）自由に選択できる。したがって、より高い値を取る方を、ヒット時の総合評価 Ah(s) として採用する。

　以上より、ステイ時の総合評価 As(s) と、ヒット時の総合評価 Ah(s) が求められた。プレイヤーは、より高い総合評価を下したオプションを選択する。

　この型のプレイヤーが一般にどのようにふるまうかを見やすくするため、仮にシューに丸々１デック残っているとした場合の、Ｃαプレイヤーの評価傾向をプロットした。

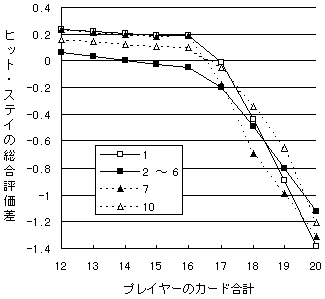
図４ ： アップカードによる、プレイヤーのヒット／ステイの評価の変化 （Ｃαプレイヤーの計算）

　凡例枠内の数字は、アップカードのバリューを示す。 一般的傾向を見るため、便宜的にシューに丸々１デック残っているものと仮定している。（現実には無いケースである。）まずアップカードのバリューが１から10の値をそれぞれとった時、先の表３の値を用い、プレイヤーのとりうるカード合計各々におけるヒットとステイの総合評価（ Ah(s) および As(s) ）を計算した。さらに両者の差を求めてプロットしたのがこのグラフである。ここでの値がプラスである限り、プレイヤーはヒットの方が有利と判断する。
　グラフより、アップカードのバリューが２〜６の場合は早めにステイしてディーラーのバストを待ち、逆にバリューが大きいかエースの場合は、積極的にヒットして勝ちを奪いに行くというパターンが見られる

　Ｃγプレイヤーは、図４をもとにした下の表に基づいて、ヒット／ステイの選択を行なう。

　表側がディーラーのアップカード、表頭が現在のプレイヤーのカード合計である。先の図４の結果をもとに作成した。単純に、図４における値がプラスならヒット、マイナスならステイを選択する。例えばディーラーのアップカードが７ならば、そのゲームにおいてプレイヤーは16以下でヒット、17以上でステイする。
　Ｃγプレイヤーはこの表によって、図４でＣαプレイヤーが示したのと同様、ディーラーのアップカードを見つつ「ステイするタイミングを遅らせる（＝ 強気に攻める）」あるいは「早めにステイする（＝ 守りに入る）」の戦法を使い分ける。ただし残りカードを参照せず、ゲーム中は一貫した判断をする。

対戦方式

　以下のように対戦を組んだ。

• ディーラー、Ａα、Ａβ、Ａγ、Ｂα、Ｂβ、Ｂγ ： 5,000ゲーム
• ディーラー、Ｂα、Ｂβ、Ｂγ、Ｃα、Ｃβ、Ｃγ ： 5,000ゲーム
• ディーラー、Ｃα、Ｃβ、Ｃγ、Ａα、Ａβ、Ａγ ： 5,000ゲーム

つまり、各プレイヤーとも合計10,000ゲームをこなした。その上で、各々の

1. 獲得チップ数
2. ブラックジャック回数
3. 勝ち回数
4. 引分け回数
5. 負け回数
6. バスト回数

を集計した。ただし 3 〜 6 は、ディーラー・プレイヤー双方でブラックジャックが起こらなかった場合に限りカウントした。

次へ（対戦結果、考察）

課題レポート類

(C) 1996 Nakamura Masaaki