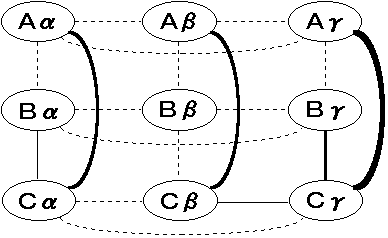
図5 : 情報収集能力と推論能力の違いによる成績の有意差
点線 = 有意差・有意傾向なし。 細実線 = 有意差。
太実線 = 強い有意差。Aγ→Cγ間はかなり強い有意差。
図の右上から左下にかけて、戦略が高度になってゆくとみてよい。
各プレイヤーごとに10,000ゲームの総成績を集計し、以下の表5を得た。
| Player | Aα | Aβ | Aγ | Bα | Bβ | Bγ | Cα | Cβ | Cγ |
|---|---|---|---|---|---|---|---|---|---|
| Chip | -1017 | -1313 | -1268 | -1034 | -1081 | -999 | -376 | -872 | -323 |
| BJ | 371 | 348 | 349 | 345 | 342 | 361 | 428 | 344 | 388 |
| Win | 3896 | 3826 | 3841 | 3927 | 3907 | 3943 | 3987 | 3936 | 3987 |
| Even | 793 | 829 | 825 | 777 | 810 | 733 | 789 | 856 | 914 |
| Lose | 4579 | 4627 | 4619 | 4572 | 4568 | 4591 | 4421 | 4491 | 4335 |
| Bust | 1205 | 1854 | 1252 | 1157 | 1088 | 1289 | 1408 | 1492 | 1941 |
各プレイヤー10,000ゲームの戦績である。表頭はプレイヤーの種類、表側は上から順に獲得チップ数、ブラックジャック回数、(ブラックジャックの時を除いた)勝利回数、引分け回数、負け回数、バスト回数である。
そして各プレイヤーの勝敗傾向を見やすくするため、表5より勝利回数と負け回数のみを抜き出し、その合計で両者をわり、ブラックジャックでなく、かつ引分けでもなかったときの勝率 p と負け率 q を求めた。( p + q = 1 )
| Player | Aα | Aβ | Aγ | Bα | Bβ | Bγ | Cα | Cβ | Cγ |
|---|---|---|---|---|---|---|---|---|---|
| Win + Lose | 8475 | 8453 | 8460 | 8499 | 8475 | 8534 | 8408 | 8427 | 8322 |
| 勝率 | 0.460 | 0.453 | 0.454 | 0.462 | 0.461 | 0.462 | 0.474 | 0.467 | 0.479 |
| 負け率 | 0.540 | 0.547 | 0.546 | 0.538 | 0.539 | 0.538 | 0.526 | 0.533 | 0.521 |
表5をもとにした、各プレイヤーの勝率と負け率を示す。
α、β、γの各情報収集タイプとも、A→B→Cの順に成績が上がっている。またA、B、Cの推論型別にみると、いずれもβタイプが一番成績を落としている。
加えて各情報収集タイプ/推論型別に勝率と負け率を集計したところ、以下のようになった。
| 情報収集タイプ | 推論型 | |||||
|---|---|---|---|---|---|---|
| α | β | γ | A | B | C | |
| Win + Lose | 25382 | 25355 | 25316 | 25388 | 25508 | 25157 |
| 勝率 | 0.465 | 0.460 | 0.465 | 0.455 | 0.462 | 0.473 |
| 負け率 | 0.535 | 0.540 | 0.535 | 0.545 | 0.538 | 0.527 |
表5をもとにした、各情報収集タイプ/推論型別の勝率と負け率を示す。
情報収集タイプについて見ると、αタイプとγタイプがほとんど同じ勝率をあげ、βタイプのみが成績を落としている。推論型別では、A→B→Cと順当な成績上昇が見られる。
さらに表6-1、6-2を元に、α・β・γ間、A・B・C間の成績の有意差を、適合度のχ2検定で検証した。
当初の設定より、情報収集能力に関しては γ→β→α の順に高度になり、推論能力に関しては A→B→C の順に高度になる。二者間の比較においては、より低い能力のプレイヤーの勝率・負け率を理論確率として設定し、それをもとにもう一方(より高い能力設定プレイヤー)の観測度数(勝ち回数と負け回数)に有意な違いが出ているかどうかを見た。
まず、情報収集能力差による違いは以下のようになった。
| A | B | C | 全体 | |
|---|---|---|---|---|
| γ→β | 0.07 | 0.04 | 4.88** | 2.89* |
| β→α | 1.72 | 0.00 | 1.71 | 2.62 |
| γ→α | 1.11 | 0.04 | 0.81 | 0.01 |
* p < .1.
** p < .05.
いずれも自由度は1である。
各推論型ごとにみる限り、Cγ→Cβ以外には、有意傾向はみられない。 Cγ→Cβ間の有意差についても、当初の設定とは裏腹に、成績が良かったのはγのほうである。 また A、B、Cのデータを総計した検定では、γ→β間に有意傾向がみられ、β→α間もあと少しで有意傾向になるところである。
次いで、推論能力差による違いは以下のようになった。
| α | β | γ | 全体 | |
|---|---|---|---|---|
| A→B | 0.19 | 2.40 | 2.21 | 4.01* |
| B→C | 4.98* | 1.25 | 9.74** | 13.92*** |
| A→C | 7.10** | 7.10** | 21.1*** | 32.78*** |
* p < .05.
** p < .01.
*** p < .001.
いずれも自由度は1である。
各情報収集タイプごとにみると、A→B間ではいずれのタイプでも有意傾向はみられず、B→C間ではαタイプで有意差、βタイプで強い有意差がみられた。A→C間ではいずれのタイプでも強い有意差が認められた。全体を総計した検定では、A→B間で有意差、B→C間、A→C間でかなり強い有意差がでた。
以上の表7と表8の結果の概略を図示すると、以下のようになる。

図5 : 情報収集能力と推論能力の違いによる成績の有意差
点線 = 有意差・有意傾向なし。 細実線 = 有意差。
太実線 = 強い有意差。Aγ→Cγ間はかなり強い有意差。
図の右上から左下にかけて、戦略が高度になってゆくとみてよい。
推論型別に見ると、いずれもβタイプが一番成績を落としている。しかしCγ→Cβ間に有意差が見られた外は、いずれの組み合わせにも有意差・有意傾向は無かった。
A型においてβタイプの成績が芳しくない点は、Aβプレイヤーが他二タイプに比べ、かなり高い割合でバストした為と考えることができる。どうやら予備試行で設定した基準値が高すぎたようだ。βタイプの場合、計算するバリューの中央値はたいがい5から動かない。(バリュー10以上がシューの過半数を超えれば、一気に10になる。半々ならば7.5。)一方αタイププレイヤーの計算する(正確な)中央値は、ゲーム中たいがい6から7の間に収まる。つまりβタイププレイヤーは、次に引くカードのバリュー中央値を実際より1〜2程度小さく見積もる傾向にある。よってαタイプと比較してこの点を補正すれば、βタイプの最適基準値は19ないし20ということになる。 つまり今回の20という最適基準値が本当に適当であったかどうかは、追試の余地があるかもしれない。
B型は χ2値を見る限り、三者殆ど同一の成績とみなしてよさそうだ。
C型はβタイプがγタイプに比べ、有意に成績を落としている。しかしγタイプよりさらに優秀であるはずのαタイプとは、有意傾向さえ出ていない。従ってこの有意差は単なる誤差である可能性があると思う。Cβタイプのみにこの種の有意差が出たことは、説明が難しい。
なおCγプレイヤーのバスト回数の多さには、目を引くものがある。引分け回数の多さとも考え合わせると、Cγプレイヤーの最終的カード合計は常に大きいものだったと思われる。これは以下のように説明できるだろう。すなわち、Cγプレイヤーがヒットを止める基準値の平均的な値 Tm は、
| Tm = | 10 Σ i=1 |
S(i) P(i) |
S(i) : アップカードのバリュー i でステイする基準値。(表4に基づく。)その値以下ならヒットする。
P(i) : アップカードのバリュー i が出現する確率。)
で示すことができる。仮にシューに丸1デック残っているものとしてこれを計算すると、Tm = 14.92 となり、アップカードを参照しない他のγタイププレイヤー(Aγ、Bγ)の基準値 14.0 よりも高めになる。つまりそれだけステイするタイミングが遅く、カード合計も大きくなったことが推測される。
ただし、バスト回数の多さにもかかわらずCγプレイヤーの成績は決して悪くない。実際には、勝率・チップ獲得額ともに、全プレイヤー中トップである。バスト回数を抑えて好成績を収めたプレイヤー(例えばCα)は、自らのバストを抑えてディーラーのバストで稼ぐ、いわば守りの勝ち方をしたのに対し、Cγプレイヤーは積極的にヒットしてディーラーと競り合う、いわば攻めの勝ち方をしたと一般に言えるだろう。ただし数字の上では、両者の成績に有意差・有意傾向は出なかった。
全体を総計した検定結果をみると、βタイプが他二タイプより成績を落とし、γタイプとの間に有意傾向を見せた。しかし、この有意傾向はCタイプでγ→β間に生じた有意差に負うところが大きく、全体としてはα、β、γの三者間に殆ど成績の相違が見られなかった、と言ってよいだろう。情報収集能力に関して対極にあるγ→α間においてすら、成績分布は偶然のぶれの範囲内に収まってしまった。これは本シミュレーションで、精密なカードカウンティングが必ずしもゲーム展開の有利な材料とはならなかった、という事を示している。
カードカウンティングが有効でなかった理由として、今回カードをシャッフルするタイミングを早めに設定したことが考えられる。先に記したルールにより、カードはゲーム開始時28枚以下のとき、52枚に戻してシャッフルする。1ゲームでプレイヤーが使うカードはたいがい2〜4枚の内に収まるので、残りカードは平均して20枚前後でシャッフルされることが多かった。これはカードカウンティングが効果を現すには、少し厳しい条件だったかもしれない。
ただし10,000というゲーム数は充分な試行数といってよく、これで有意差・有意傾向がほとんど見られなかったことは興味深い。カードカウンティングの有効性はカードゲーム全般で言われる事だが、少なくともブラックジャックでは単なる骨折り損に過ぎない可能性が示された。
各情報収集能力タイプごとに見ると、A→B間にはいずれも有意傾向が見られなかったが、A→C、B→C間には殆どのケースで有意差が見られ、C型推論が有意に好成績をあげたことが見て取れる。
全体を総計した χ2検定では、さらにC型推論の優位性が明らかになる。またここではB型推論にも若干の優位性がみられる。
各戦略の情報利用の柔軟性についてまとめると、以下のようになるだろう。
| A | B | C | ||
|---|---|---|---|---|
| 変数 | シューの残りカード (*) | ○ | ○ | ○ |
| 現在のカード合計 | ○ | ○ | ○ | |
| 現在のアップカード | - | - | ○ | |
| 定数 | カード合計からの配当期待値 (表1) | - | ○ | - |
| アップカードからの最終カード合計の見込み (表3) | - | - | ○ |
(*) γタイプのプレイヤーは、これも定数とみなす。
A型とB型との比較をするならば、言うまでもなく「カード合計からの配当期待値 」(表1)という 定数を利用する 点でBが有利である。これによりB型プレイヤーは、A型よりも微妙なヒット/ステイの判断を行なうことができるようになった。(シューの中身を把握しているα、βタイププレイヤーは、特にそうである。)しかしα、β、γの各タイプ別ではAB間に有意傾向は出ず、全体の総計でようやく有意差が見られた。つまり表1の利用にはさほどの効果が見られなかったといえる。
一方C型は、表1の値をさらに「現在のアップカードのバリュー」と「アップカードから予想される、ディーラーの最終カード合計の見込み(表3)」の二つの要素に分解し、前者を 変数として その場ごとに再計算している。つまり状況への対応の柔軟性という点で、より優れた方法をとっている。χ2検定による対戦成績の分析(表8)は、これが他の二つの推論型に比べ、有意に効果的だったことを示している。
情報収集能力別に見ると、αタイプとγタイプではA型・B型両方に対し、βタイプではA型に対し、有意差を示した。また全体を総計した分析では、A型・B型両方に対し 0.1% 水準のかなり強い有意差が出た。
以上の結果は、ディーラーのアップカードを参照し、ゲーム毎に「強気に攻める/守りに入る」の戦略を使い分けるC型推論の有効性を示している。
次へ(現実への適用)
(C) 1996 Nakamura Masaaki