正二十面体の面を延ばすと、非常に複雑に互いに交わります。

上図はicocelに同梱の解説図です(色は元の図にはありません)。
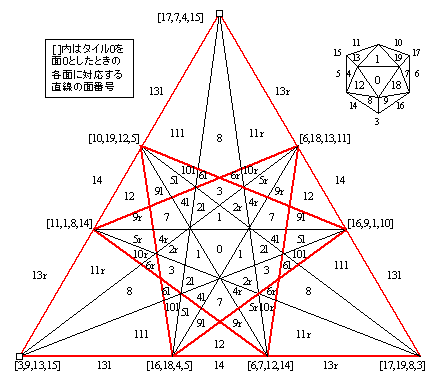
まず、真ん中の0の番号が付いた逆三角形は、元の正二十面体の面の一つです。他の面の延長との交わりは直線で表されています。[
]内の数字は面番号で、右上の正二十面体の図の番号と同一です。たとえば、0番面の上辺は1番面との境で、左右の[
]内に1があるのは1番面との交わり、との意です。左上の長い直線(□が端に付いているもの)は0番面と15番面の延長の交わりです。対称面とは平行で交わりませんから、結局、18本の直線で交わることになります。
切り取られた面はregion(本プログラムでは「タイル」)と呼ばれています。最も内側の0番タイルは元の正二十面体の面(face)そのものです。すぐ外側に1番タイルが3つあります。タイル番号と面番号(本プログラム特有)は関係ないことに注意ください。1番タイルは二等辺三角形です。
2番タイルは不等辺三角の左右対称のペアが3枚ずつあります。左右を区別するため、rとlの文字が付いています(オリジナルでは字体で区別される)。
3番タイルは凧形四辺形です。以下、14番までタイルに番号が付いています。13番と14番は上図の赤い線を延長してできる、外側のかなり大きな三角形です。
タイルで囲まれた空間は、「セル」と呼ばれています。セルはまるで玉ネギのように層になっていて(ずいぶんとげとげのような気もしますが…)、まず中心部に元々の正二十面体があり、Aと名づけられています。次の階層はbと呼ばれ、Aに被せるとBと呼ばれる立体になります。以下、セルの階層はc, d, e, f, g, hと続き、それぞれC, D, E, F, G, Hと呼ばれる立体が構成されます。
b, c, d, hは完全に表面を覆ってしまい、外から見ると立体B, C, D, Hと区別が付きません。e,
f, gは2種のセルからなり、それぞれ、e1, e2, f1, f2, g1, g2と名づけられています。さらに、f1には左右対称のペアがあり、本プログラムではf1rとf1lとして区別されます(オリジナルでは字体で区別される)。
e, f, gはそれぞれ二種あるので、片方だけ選ぶと穴が開いてしまいますから、外から中へ入ってゆくことができます。そのために、正二十面体の星形は変化に富んでいるのです。
添え字の数字は大変巧妙に付けられていて、星形を考える場合は必ずe1-f1-g1またはe2-f2-g2の系列で現れます。その理由は自明ではありません、icocelの表示をながめながら理由を考えてみると面白いと思います。
左右非対称の立体はf1rまたはf1lの片方を選ぶと作られます。この場合、f1rを仲介として1系と2系が混じることがあります。
徹底的な探索の結果、正二十面体の星形は58種ある、ということになり、元の正二十面体と合計して「59の二十面体」という本(英語です)にまとめられました。本プログラムicocelでは、そのすべてを見ることができます。
タイルとセルの関係は自明ではありません。幸い、「59の二十面体」に構成が載っています。詳しくは、オリジナルの本を取り寄せるのが最良ですが、icocelに同梱のReadMe.txt、ReadMeD.txtにも要約が載っています。
2002年7月20日 岡田好一