開平法
基本の考え方
展開
はじめに単純な展開で説明します。 次の式が成り立ちます。
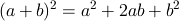
この式を用いると2桁の平方が各位の数を用いて計算できます。 たとえば67の平方の場合は67を60+7として次のように計算できます。
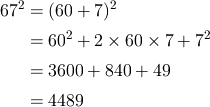
最初の展開式は次のように一般化できます。
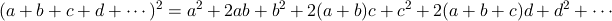
開平と展開
開平する実数を
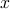として
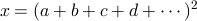
が成り立つとします。 このとき
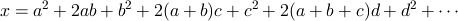
が成り立ちます。 開平法ではこの展開式をもとにして各位の数を求めていきます。
倍根法
考え方
開平する数に対して倍根の除算と平方減を繰り返す開平法です。 開平法の基本になります。
展開式
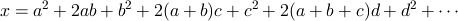
をもとにして考えます。
倍根が
、
、
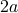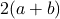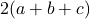…平方減が
、
、
、
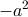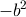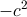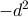…に相当します。
そろばんによる計算例
4489の開平を例に説明します。
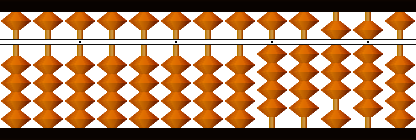
開平する数を小数点の位置から2桁ずつに区切り、最高位2桁44の平方根6を初根として立てます。
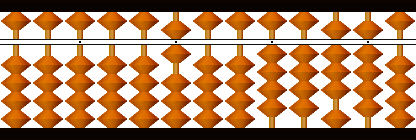
初根6の平方36を引きます（平方減）。
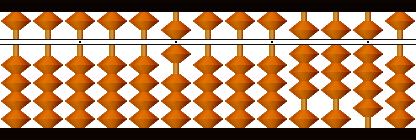
初根6の2倍12（倍根）をおきます。
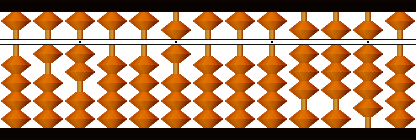
残り88を倍根12で割り、商7を次根として初根のとなりにおきます。
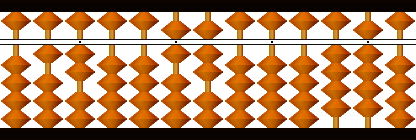
次根7の平方49を引きます（平方減）。
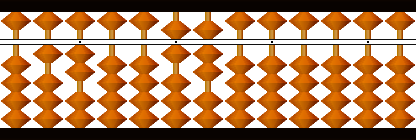
次根7の2倍14を倍根に加えます。
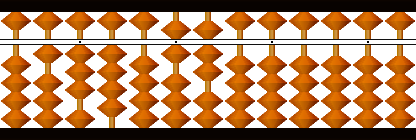
4489の平方根が67とわかります。3桁以上の場合はこの繰り返しです。
半九九法
考え方
開平する数に対してはじめに平方減を行い、半分にしてから根の除算と半九九減を繰り返す開平法です。 はじめに平方減を行わない方法もあります。 慣れると倍根法よりも早いといわれています。 半九九とは九九の半分の数のことです。 たとえば5の半九九は12.5です。
展開式
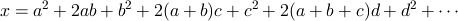
の右辺第1項を左辺へ移項します。
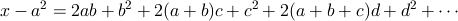
これがはじめの平方減です。
次に両辺を2で割ります。
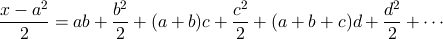
半九九法はこの式をもとにして考えます。
根が
、
、
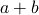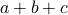…半九九減が
、
、
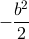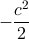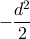に相当します。
倍根法が除算のために倍根を計算して保持しなければならないのに対して、半九九法は根（求める平方根）そのもので除算を行えばよいため効率的です。
そろばんによる計算例
倍根法と同様、4489の開平を例に説明します。
開平する数を小数点の位置から2桁ずつに区切り、最高位2桁44の平方根6を初根として立てます。
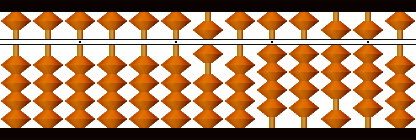
初根6の平方36を引きます（平方減）。
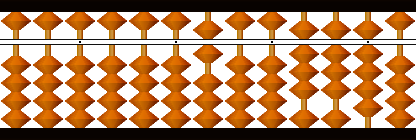
残りを下位から半分にしていきます。
9→4.5
8→4
8→4
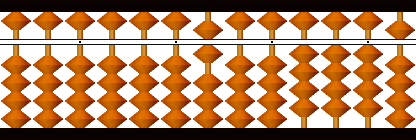
残りを初根6で割り、商7を次根として初根のとなりにおきます。
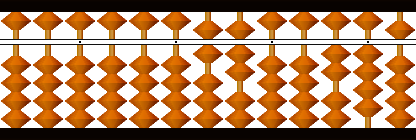
次根7の半九九24.5を引きます（半九九減）。
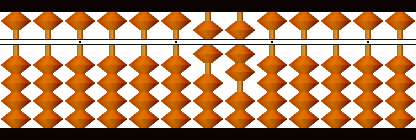
4489の平方根が67とわかります。3桁以上の場合はこの繰り返しです。