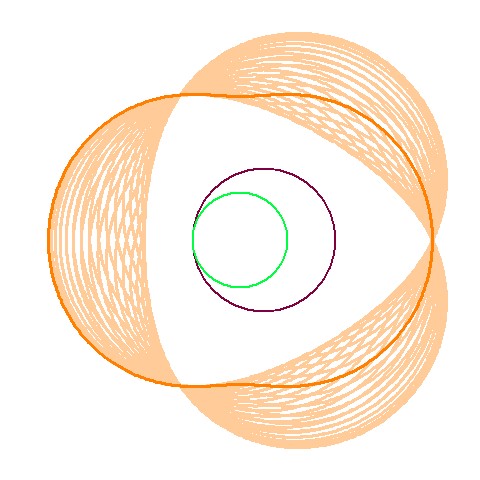
ロータリーエンジンを描く
ロータリーエンジンとエピトロコイド曲線
ここではローターとローターハウジングを描くことにします。 ローターハウジングはエピトロコイド曲線(epi trochoid)です。 エピトロコイド曲線は固定された基円に外接して回転する、転円に固定された点が描く軌跡の事です。 ローターは転円に内接したまま基円を回転させたときの、基円に固定したエピトロコイド曲線の内包絡線となります。 ロータリーエンジンでは基円と転円の半径の比が2:3となります。 いずれの曲線も複雑なもので人力で描くのは大変です。 そこで今回は関数グラフソフトであるFunctionviewを用います。
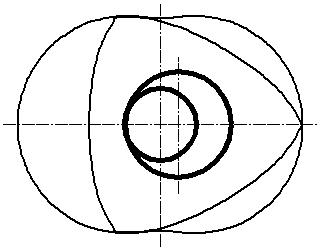
記号を以下のように定めます。 円Aが基円、円Bが転円で点Cで円Aと接しています。 円Aの半径がp、円Bの半径がqです。 点Pは円Bに固定されています。 回転方向は左回りを正とします。
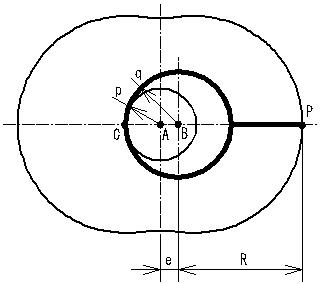
ローターハウジングを描く
下図はエピトロコイド曲線を描く途中で、点Cが円Aのまわりを180°回転した位置にきています。 このとき円Bは円Aに対して60°回転しています。 これは円Aと円Bの半径の比が2:3だからです。 すなわち円Bの半径が無限大な場合に円Bは円Aに対して180°回転するところを、滑らず回転する事でさらに-120°回転しているのです。 180°と120°はちょうど半径の逆比になっています。 点Cが円Aのまわりを1080°回転したところで円Bは円Aに対して360°回転し、点Pは元の位置に戻ります。 ローターハウジングはこの点Pの軌跡になります。
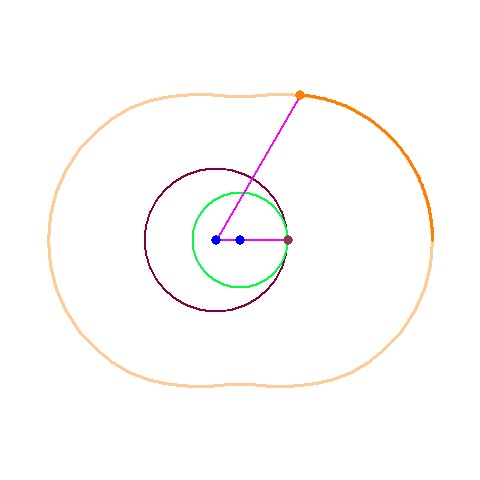
ローターを描く
先ほどとは逆に円Bを固定し円Aを回転させます。 このときエピトロコイド曲線を円Aに固定したまま回転させます。 下図はエピトロコイド曲線の内包絡線を描く途中で、点Cが円Bのまわりを-120°回転した位置にきています。 このとき円Aは円Bに対して60°回転しています。 これらは先ほどと似た関係になっています。
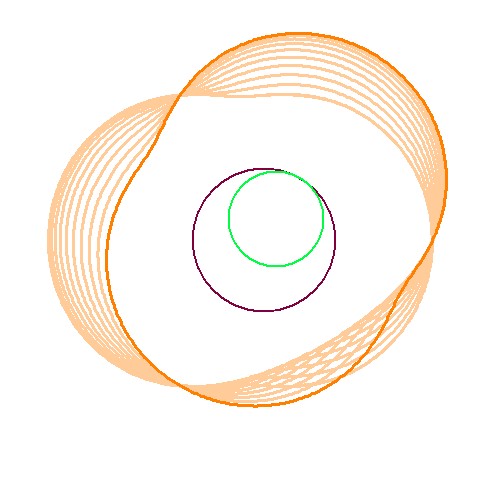
下図では点Cが円Bのまわりを-360°回転して元の位置に戻ってきています。 上図の3倍回転したわけで、円Aは円Bに対して180°回転しています これは上図で右下部分の包絡線が完成している事からも分かります。 ローターが一回転する間には上図の3倍の回転を必要とするはずです。 ここで右下部分の包絡線が完成したという事はちょうど一回分の出力があったことになります。 つまりローターが一回転する間に3回の出力行程があることになります。