あなたも LoTTer ? Part2
| まえおき |
| LoTT の歴史 (1) Jean-René Vernes |
| LoTT の歴史 (2) Larry Cohen |
| LoTT の歴史 (3) Matthew Ginsberg |
| 問題点 |
| 自分流の LoTT 分析 |
| Ginsberg の研究を追試する |
| ２本立ての分析 |
| 細かい注意 |
| スート 対 スート |
| ノートランプ 対 スート |
| LoTT は HCP に依らず成立する |
- おや，また LoTT の話が続くのですか ?
―― はい。これまで ちょっと気にかかっていたことが ありました。
そこで，ソフトウェアを一つ書いて 調べました。その結果 得られた内容を ここに書こうと思います。 およそのことは既に (前篇に) 書いたのですが， ここできちんと報告しましょう。 - 気にかかるとは，どんなこと ?
―― その前に， LoTT の歴史をざっと復習しておきましょう。
- そもそも，ブリッジというのは，モーム (W.S.Maugham，1874-1965) が何か有名な言葉を言ったらしいから，ずいぶん古い
歴史を持つような印象を受けますね。
―― 今の形式のコントラクトブリッジが成立したのは，ものの本によると, 1925 年です。そして 1940 年代には，ポイント･カウント法の導入により, ブリッジは急速に普及しました。
LoTT が提唱されたのが 1966年。 今から 約 50年前のことです。今となっては，どちらも昔のことと言えるでしょう。
Larry Cohen が強調しているように，ポイント･カウントと LoTT は，どちらも 今のブリッジに 欠かせない要素です。
LoTT の歴史を辿ると，3 人の名前が挙がります。
この 3 人が LoTT に果たした役割は，Jean-René Vernes, Larry Cohen, Matthew Ginsberg. (1966) (1992) (1996)
発見･提唱， 普及， 検証
と言えるでしょう。LoTT の歴史 (1) Jean-René Vernes (1966)
「合計トリック数」という革新的な概念に目をつけたのは，この人でした。 ブリッジは，双方が取るトリック数の 差 を争うゲームです。したがって， トリック数の 和 が意味を持つなどとは，誰も想像できません。
Vernes は，この合計トリック数について，次の法則を発見し，これを 「合計トリック数の法則」(the Law of Total Tricks, LoTT, la Loi des Levées Totales) と 呼びました (原文)。
[1] スート 対 スート の場合
合計トリック数 ＝ 双方の切り札の合計枚数
[2] ノートランプ 対 スート の場合
合計トリック数 ＝ スート 側の切り札の枚数 + 8, 7, 6.
ここで右辺に書かれている 3 個の数値は，スート側がサイド･スートに ボイド，シングルトン，ダブルトン をそれぞれ持つ場合に対応します｡
原著では，LoTT 公式 [2] が上のような見やすい数式ではなく，場合分けをした表として与えられており，複雑な印象を与えます。
これらの法則の発見の仕方が演繹 (推論) によるものと期待して, 私は Vernes さんの本を € 31.37 で 取り寄せたのですが，期待に反して，それは帰納によるものでした。つまり，10 年間にわたる世界選手権戦のハンド記録を丹念に調べて，上の法則が 統計的に 成り立つことを確かめたのです (この「統計」という修飾語は，Vernes 自身が使っています)。
今の世の中ならば，居ながらにしてハンド記録を収集したり, PC を使ってデータ処理をすることは可能でしょう。でも，1960 年には, もちろん，PC はおろか，電卓も ありませんでした。そういう中でのこれだけの作業は，想像を絶するものがあります。それだけ, LoTT に深い関心を抱いていたのでしょう。
さらに，これに加えて，Vernes は,「安全な代の規則」
｢味方の切り札の合計枚数に相当する代まで安全に競り合うことができる｣
も発見しました。この規則は，競り合いのビッドで非常に重要ですが, 本稿ではこれには触れず，法則 (LoTT) だけに注目します。
LoTT の歴史 (2) Larry Cohen (1992)
Vernes の著書は 今 読んでも十分説得性がありますが，フランス語で書かれたのが致命的でした。 このため，長い間 日の目を見ることがありませんでした。
結局のところ，LoTT に最初に注目したのは Marty Bergen でした。そして，Bergen が Larry Cohen と知り合うようになってから LoTT が次第に普及し，遂には Cohen の 2 冊の著書によって世界中に LoTT が知られるようになりました。
この著書では，法則 と 規則 のあいだの関係が チャート により明確化されました。
これについて，Vernes の著書には全く説明が無く，法則と規則のあいだの関係が きちんと説明されずに残っていました。チャートのロジックは，この間の橋渡しとして重要な役目を果たし，LoTT を普及する上で大きな力になりました。
LoTT を理解して実際に応用するためには，
LoTT 公式, 規則, チャート
この 3 つを理解する必要があります。このため，現在では,「LoTT」という表現の中に，この 3 つが同時に含まれることが多いようです｡
ノートランプの場合について，Cohen は Vernes 公式 [2] を簡略化して
[3] 合計トリック数 ＝ スート側の切り札枚数 + 7
としました。ボイドやシングトンは，調整 (adjustments) として考えればよい という立場です。
LoTT の歴史 (3) Matthew Ginsberg (1996)
Vernes のように，実際にプレイされたハンドを調べる代りに，コンピュータを使って大規模な 統計的 検証を行ったのが，Ginsberg です。
彼は，ランダムに発生させた 446,841 個のディールに対して， 自らが開発したダブルダミー分析器を用いて，LoTT の検証を行いました｡ (ダブルダミー分析とは，すべてのプレイヤーが最善のプレイをすると仮定して， それぞれ何トリック取れるかを分析することを言います) 。その結果は，Vernes の発見を正確に 裏付けました。
その論文には，結果の数値だけが載っており，グラフは無いのですが，これを 私の手でグラフ化したものを， ここをクリック[別画面]してご覧下さい。
このグラフの縦軸と横軸は，それぞれ，LoTT 公式 [1] の左辺と右辺を意味します。 したがって，傾き 45° の斜め直線が 公式 [1] を表します。平均値を表す ×印が直線上によく載っている ことが分かります。
- ずいぶん良く合っているようですね，このグラフは。
―― はい。 縦の棒線が「エラー･バー」と呼ばれるもので， 平均誤差を表します。切り札の枚数が 20 以上だと誤差が大きくなりますが，これは，そういうディールのサンプルが少ない (頻度 Frequency が低い，稀にしか出現しない) ためです。
- 良く合っていて，問題無いように見えますが，ぼこさん，何か気にかかることでもあるんですか ?
―― はい。 ここから先は，私の気にかかる点を挙げて， 私なりに それをどう解決したかを説明していきましょう。要するに，Ginsberg の統計的検証を精密化したいのです。
細かいことまで挙げると キリがないので，大きな点を 2 つ挙げます。(1) 上のグラフは，確かによく合っています。でも，ここで 「切り札」として 何を採用しているかが問題です。 Ginsberg は 面倒なので，最長スートを 切り札としました。上の結果は，そうして得られたものです。つまり，LoTT 公式として
[A] 合計トリック数 ＝ 双方の切り札の合計枚数の代わりに[B] 合計トリック数 ＝ 双方の最長スートの合計枚数を採用しました。
このため，たとえば，4
と 4
が
どちらも可能で， の方が長い場合には，コントラクトがゲーム未満の 4 となり，切り札枚数として， の長さが採用されます。でも，これは
現実のブリッジのビッドに反します。
- 確かにそういうことになりますね。 上の結果は，LoTT 公式として [A] ではなしに [B] が
良く合うことを確かめたわけか …。
それで，2 番目の問題点は ?―― (2) ノートランプ (NT) に関して，次の 2 つの問題があります。
(2-1) NT の場合の LoTT 公式が未検証である。
(2-2) NT をビッドする可能性を排除して，全てのハンドがスートをビッドするとして取り扱った。
- そういう検証をするには，Ginsberg と同じ / または それ以上のソフトウェアを
開発する必要がありますね。
―― 有難いことに，Ginsberg は，自分の論文と同時に，717,102 個のディールと そのダブルダミー分析結果とを ライブラリ･ファイル (18 MB) として 彼のサイトに 残しました。
これを使えば，誰でも，自分流の LoTT 分析ができます。
- そうやって「ぼこさん流」の分析をなさるのは結構ですが，でも，
Ginsberg の結果と 比べることが 先決でしょう。
―― はい。その通りです。
何かの研究をする場合，これまでの他の人の結果を 再現できることが，まず第 1 に必要です。つまり，追試しなければいけません。
追試に当たっては，Ginsberg と同じ条件を設定します。すなわち，
(1) 双方とも，最長スートを切り札とする。
(2) ノートランプの可能性を，全く考えない。
たとえば，6NT できるハンドが スートでは 2 しか
できない場合，コントラクトを 2 として， の枚数を公式 [B] に当てはめる。
- いくらなんでも，それはちょっと乱暴な …。
―― 確かに乱暴ですが，さっきのグラフは，この設定で得られたのです。
ともかく，この設定で，私のソフトウェア (LoTTanalyzer) を実行して， Ginsberg の結果と比較しました (グラフによる比較では不十分なので，数値を比較します)。
左側は，Ginsberg の論文の値そのものです。 右側は，私の結果です｡ (ここで，サンプルのサイズが Ginsberg の 446,741 と合わないのが，不思議 です。Ginsberg が論文で使ったライブラリは，別物だったのでしょうか)LoTTanalyzer による Ginsberg の結果の再現 Ginsberg (total.ps.gz) LoTTanalyzer
( Ginsberg + Length Option)長さ ハンド
個数ずれの
平均値平均
誤差長さ ハンド
個数ずれの
平均値平均
誤差14 46,944 −0.15 0.63 14 75,608 −0.15 0.63 15 47,281 −0.14 0.64 15 75,592 −0.14 0.64 16 120,525 0.10 0.70 16 193,690 0.10 0.70 17 102,184 0.02 0.75 17 163,632 0.02 0.75 18 69,792 −0.01 0.83 18 111,997 −0.01 0.83 19 37,561 −0.22 0.87 19 60,416 −0.21 0.86 20 15,845 −0.50 0.99 20 25,545 −0.50 1.00 21 5,041 −0.89 1.20 21 8,123 −0.89 1.20 22 1,286 −1.31 1.48 22 2,035 −1.28 1.46 23 237 −1.78 1.83 23 396 −1.83 1.87 24 45 −2.22 2.27 24 68 −2.22 2.25 合計 446,741 −0.05 0.75 合計 717,102 −0.05 0.75 - とても良く合っていますね。ということは，追試は成功 …。
―― はい。驚くほど良く一致します。
なお，ここでは Ginsberg の追試をするため，HCP に制限を設けず，全てのディールを分析の対象としました。しかし，HCP の差が大きければ, 現実には，競り合いは発生しません。
そこで，以下の分析では，両者の HCP を 15〜25 HCP の範囲に限定します。このため，分析の対象となるディールが減少します。
- ２本立てというのは，多分 ノートランプを別扱いするということでしょう …。
―― さっきのような乱暴はやめて，NT の方が有利なら，そちらを選んでやりましょう。 つまり，ハンドを [Suit vs Suit] と [NT vs Suit] のどちらかに分類します。
ただし，NT で 5 トリックしか取れないような バランス･ハンドまで [NT vs Suit] に 分類するのは，どう考えても不自然です。そこで，2 つの条件をつけて分類します.
[1] NT コントラクトで 7 トリック以上取れる。
[2] NT でのスコア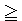
スートでのスコア
- ということは，つまり， …，たとえば，3NT と 4 が
どちらも可能なハンドは，4 と分類するし，3NT と 5 が
どちらも可能なハンドは 3NT に分類する。
―― それが，自然なビッド経過に合致します。
スートの長さではなしに，コントラクトの スコアを 基準にしてプログラムを作ると，上のような分類が可能になります。
こうして，717,102 個のハンドが 501,591 + 215,511 個に分別されます。 このように スコアを判断基準にすると，前に触れた例( 4 と 4 の
どちらも可能で の方が長い場合) では，4 が自然に選択されます。
細かい注意
プログラムを作ると，この他にも細かい注意が必要なことが分かります。
(1) 競り合いの結果，低いスコアのコントラクトを選ばざるを得ないことがあります。
たとえば，3 と 4
が どちらもできるハンドを考えましょう。
このとき，スコアの大きい 3 が自然なコントラクトです。
しかし，相手方が 4 をビッドすると，こちらは，4 に上がる (スコアは下がる) 必要に迫られます。このような変更は，一般に，LoTT 公式で採用される切り札枚数を変更します。
(2) 通常は，ペアのうちのどちらがディクレアラーになっても，取れるトリック数は同じ値ですが， ハンドによっては，これが違います。つまり，一般に，トリック数は，オープニング･リードがどこから打たれるかに 依存します。
このような場合，Ginsberg は，より多くのトリックを取れるプレイヤーをディクレアラーに指定します。 けれども，これは正しくありません。
LoTTanalyzer では，トリック数が異なる場合，ディクレアラーに次の条件を課しました。
[1] パートナーよりも長い切り札を持つ ( したがって，そのスートを最初にビッドする可能性が高い )。
[2] 切り札の長さが同じならば，より多くの HCP を持つ。
[3] NT の場合には，パートナーより多くの HCP を持つ。 - なんだか こまごましていて頭が痛くなりそう …。
―― プログラムを作りながら考えていくと，簡単そうに見えていた作業が複雑になっていきます。 でも，基本は，スコアを基準にして，なるべく自然なビッド経過に合わせたいのです。
- 早く結果の方を見たいですね …。
―― はい。では，二本立ての片方から …。
- これが，Suit-Suit の場合の結果ですね。
―― はい。 上に説明したように いろいろと工夫したのが，下表の右側の数字です。
左側は，さっきと同じ Ginsberg の数字です。ここでは，切り札枚数により分けずに， 全体について数字を挙げました。 ここで ずれ (deviation) と書いているのは，
ずれ ＝ 合計トリック数 − 切り札の合計枚数
です。 Ginsberg の場合には，もちろん
ずれ ＝ 合計トリック数 − 最長スートの合計枚数
です。これをすべてのディールについて平均したものが，Average deviation (ずれの平均値) です。Ginsberg と LottAnalyzer の結果を比較 Ginsberg
(total.ps.gz)LoTTanalyzer
(Standard)+1 トリックのずれ 22.4% 31.5% 0 トリックのずれ 40.0% 38.8% −1 トリックのずれ 24.5% 14.9% ずれの平均(tricks) −0.05 +0.37 平均誤差(tricks) 0.75 0.79 標本サイズ 446,741 389,908 - +1 トリックの ずれ というのは，過大 / 過少のどちらなのかな ?
―― LoTT が期待するよりも，実際に取れるトリックが多いということですから， LoTT の評価が過少だという意味です。
- この 2 つの結果を どういうふうに比較するんですか ? 私は統計に詳しくありませんから …。
―― 統計データを見るときには，データの ばらつき具合に注目することが大切です。
統計から出るのは あくまでも何かの平均です。平均として何かの結論が出たとしても，データの ばらつきが大きければ，それを平均しても， あまり意味がありません (統計学の言葉を使えば，有意でない)。それに対して，ばらつきが小さければ，(たとえば，何かの 直線，曲線の上にデータ点が良く載っていれば)，そこから得られる結論は有意です (大いに意味がある)。 - ぼこさん，なんだか，統計の先生みたい …。
―― もうちょっとだけ続けると …
このばらつきを表すのが，ここでは， 平均誤差です。 その定義は 簡単です｡「ずれ」の絶対値を すべてのディールについて平均したものが，平均誤差です。 絶対値を平均するので，+ にずれても − にずれても，平均誤差は大きくなります。 - それで，その 平均誤差のところを見ると，左では 0.75, 右では 0.79 トリックと
なっていますね。これを，統計の立場から どう読むのですか ?
―― 2 つの異なる結論を比較する際には，そのばらつきを比較します。 ばらつきの小さい方が信頼性が高い。大きい方が信頼性が低い。この判断基準は， 後にも出てきます。
今の場合は，左の 0.75 の方が 右の 0.79 より小さいので，左の方が少しだけ信頼性が高いと言えます。 でも，0.75 と 0.79 はほとんど同じ数値ですから，両者の信頼性はほぼ同等と考えてよいでしょう。 - なるほど，そういうふうに考えて統計分析の結果を読むわけか …。
―― そういうわけで，この比較に関する限り，私の努力は，あまり報われませんでした。
- どういうことですか ? ぼこさん。
―― 上にも書いたように，左では NT を完全に無視して，どのハンドもスートで ビッドすると仮定している; 切り札の選定にも不自然さがある ―― こういう欠点を 克服すれば，何かばらつきの小さい (もっと信頼性の高い) 結論が得られるのではないか … というのが， この作業に手を染めたきっかけです。
あっ，ちょっと脱線気味ですね。 - でも，ぼこさんの「おもい」は分かるような気がします。
それで，両者の信頼性が同じ程度だということにして，ここから得られる結論は どうなるのですか ?
それから，左側の場合のグラフは，さっき見せてもらいました。
右側の方も同じようなグラフにすると，どうなのですか ? 数字よりも，グラフの方が分かりやすいですからね。―― では，両方のグラフを並べて見ましょう。
グラフの縦軸と横軸の意味は，さっき説明しました。ただし，この図に書き込まれているように， 左では，横軸に Total Length (最長スートの合計枚数) を取り，右では，横軸に Total Trumps (切り札の合計枚数) を取っている ―― これが，大きな違いです。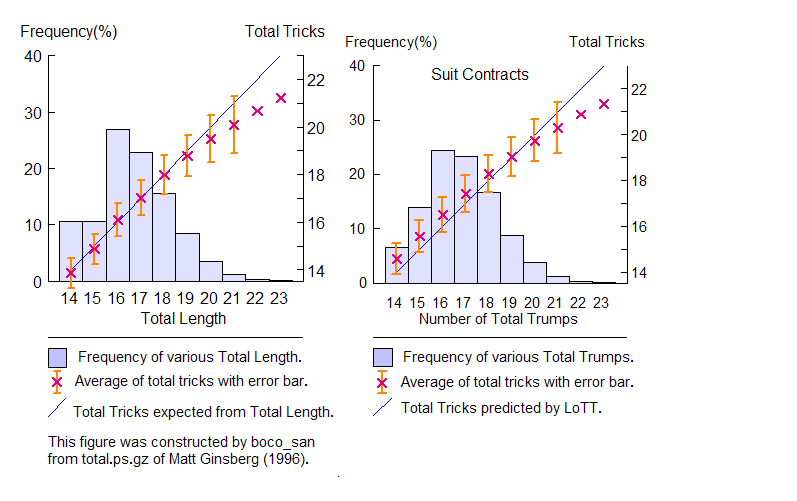
この 2 つのグラフは，それぞれ異なる結果を主張します。 - そのどちらも，信頼性が同程度なのですね。
―― はい。その通りです。
左側については，さっき説明しましたが，繰り返すと，× マークが傾き 45° の直線上に非常によく載っていることから分かるように，
LoTT 公式として [B] を使えば (使えれば) ,《平均的に見て》 調整の必要は全くありません。 - ここで，《平均的に見て》という注釈が入ったのは，なぜですか ?
―― さきほど説明したように，統計分析の結果というのは，平均だけを主張します。 つまり,「平均として調整を要しない」という表現の意味は，プラスに調整することもあれば， マイナスに調整することもありうる ―― でも，それを何回もすると，平均はゼロである … という 意味です。
- えっ，なんだか，私が漠然と思っていたのとは違うような …。
―― でも，統計というのは，本来そういうものなのです。人口の統計でも, 経済の統計でも …。
- じゃぁ，一回一回の調整の大きさは，どのくらいにすればいいんですか ?
―― これは統計的な分析ですから，いちいちのハンド･ビッド状況については， 何も言うことができません。上の表から分かることは， 公式 [B] を出発点とすれば，全く補正しないハンドが 40.0%， +1 の補正を必要とするハンドが 22.4%， −1 トリックの補正を必要とするハンドが 24.5% の確率で，それぞれ現れます。
- 右側も，これと同じように読めばよいのですね。
―― はい。右の場合には，普通の LoTT 公式 [A] を出発点として 判断する。
そのとき，+1 トリックの補正を必要とするハンドが，−1 トリックの補正を 必要とするハンドの 約 2 倍出現する。そこで，《平均的に見て》 +0.37 の補正が 必要になる。+2 以上とか −2 以下の場合は，この表では省略されています。 - これまでに,「補正 (corrections)」とか「調整 (adjustments)」という言葉が何度も出てきましたが，
Larry Cohen が言っている「調整」との関係は, どうなのでしょうか ?
―― 答は (ちょっと物理屋さんの用語をお借りして) 《相補的》complimentary です。つまり，互いに補いあって，どちらも意味を持ちます。
Cohen は，その 2 冊の著書の中で，adjustments の必要性を強調しています (これは， LoTT の創始者である Vernes も同じです)。 ハンド例を挙げて，いろいろの 正負大小の調整理由を述べています。ハンド毎にひとつひとつ調整の必要性を判断します。 その話が細かくなると，ちょっとついて行けないような印象も受けます。
一方，Ginsberg や私の分析では，調整理由は不明ですが， 統計的に見て, どういう頻度でどういう調整をするのがよいかを教えてくれます。
たとえば，右側の場合 (すなわち，本来の LoTT 公式 [A] を額面通りに使う場合)，+1 の調整を要するハンドは，−1 の調整を必要とするハンドの 2 倍現れる。 39% のハンドでは，調整を要しない。これらは《統計的に確実な》ことです。このような数字は，Cohen の分析からは得られません。
以上が，Suit-Suit の場合について得られた結果です。
次に，ノートランプの場合に話を進めましょう。
- ノートランプの場合の LoTT 公式は，はじめのところで説明がありました。
[C] 合計トリック数 ＝ スート側の切り札枚数 + 7これが Cohen の本に書かれている公式です。
ところが，LoTT を発見した Vernes が最初に言ったのは，[D] 合計トリック数 ＝ スート側の切り札枚数 + 8, 7, 6.―― はい。 ここで 右辺に 3 個の数値が書かれているのは，スート側がサイド･スートに ボイド， シングルトン，ダブルトン をそれぞれ持つ場合に対応します。
- それで，たぶん前篇に書いてあったと思うんですが，このボイトとかシングルトンは，ディクレアラー，ダミーのどちらでもよい …。
―― はい。Vernes は，はっきりと そう書いています。
ダミーに ボイド，シングルトン があれば，ラフ により トリック数が増える。 ディクレアラーに ボイド，シングルトン があっても，トリック数は 増えない … それにも拘らず，上の LoTT 公式には この両方を含めてカウントします。 - それで，ぼこさんのソフトウェアを使うと，この 2 つの LoTT 公式のどちらが良いか
分かるんですね。
―― 分かったのですが，どちらも，あまり良くない結果です。
そこで，Vernes の公式 [D] にちょっと手を加えて，[E] 合計トリック数 ＝ スート側の切り札枚数 + 9, 8, 7.としてみました。つまり，右辺に 1 を加えたのです。私のソフトウェアでは，これを "Modified Vernes Formula" と 呼んでいます。 - それでは，3 通りの LoTT 公式 [C, D, E] を比較できるわけですね。
その結果は，どうなりますか ?―― さっきも説明したように，平均誤差を見る必要があるので，グラフではなしに， 数値の比較をしましょう。
ここでは，さっき説明した手順に従って，ノートランプのディールだけを抜き出して集計しました。 また，双方の HCP の範囲を 15-25 HCP に限定しました (実際には，この限定は不要なのですが)。Results of LoTTanalyzer for Notrump Contracts Law Formula Cohen [C] Vernes [D] Modified Vernes [E] +2 trick deviation 13.5% 21.5% 5.0% +1 trick deviation 32.5% 40.8% 21.5% 0 trick deviation 37.3% 25.4% 40.8% −1 trick deviation 11.4% 5.9% 25.4% Average Deviation 0.62 tricks 0.95 tricks 0.05 tricks Average Error 0.87 tricks 1.09 tricks 0.73 tricks Sample Size 145,140 145,140 145,140
HCP があまりにも違うと，競り合いは発生しないと考えたからです。 - さきほどの統計の考え方に従って，真っ先に 平均誤差 (Average Error) を読むと，
0.87，1.09，0.73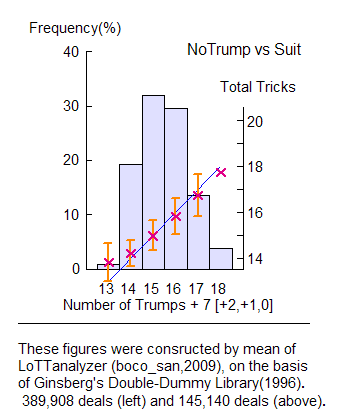
だから，公式 [E] の信頼性が一番高い … ぼこさんの努力が報われましたね｡―― はい。そういう結論が出て，ほっとしたところです。
右のグラフは，[E] の場合です。
このグラフから，公式 [E] を使えば 《平均として》補正を必要としないことが，分かります。
念のために書き加えておくと，[E] を使って補正を必要としないハンドは, 確率 40.8% で 発生します。[E] から +1 トリックの補正を必要とするハンドは，確率 21.5% で発生し， −1 トリックの補正を要するハンドは，それとほぼ等しい確率 25.4% で発生する … と いうのが，ここでの結論です。
サンプルのサイズが非常に大きいので (145,140個) これらの確率の数値は 非常に正確だと考えてよいでしょう。得られた平均誤差についての補足
(1) NT の場合，[E] について得られた平均誤差は 0.73 トリックです｡ これを，Suit の場合の表と比べてみると，Suit vs Suit では， 0.79 トリックとなっていました。両者の数字がほぼ等しいので，どちらの結論も同程度の 信頼性を持つと考えられます (この結論は，プログラムの作者をかなり 安心させました)。
(2) Vernes の公式 [D] が最も悪い，という結果になったのは，意外であり， 残念でした。なぜなら，前にも書いたように，Vernes は 10 年間にわたり累積された 一流プレイヤーのハンド記録を分析して，この公式 [D] を導いたからです。
この齟齬の原因は，サンプルの大きさにあります。ハンド記録をもとにする場合， ひとつのディールが Open Room では NT でプレイされ，Closed Room では スートで プレイされる必要があります。
そういうディールは，現実には，Suit vs Suit に比べて 遥かに少ない。Vernes の記述によると，Suit vs Suit では 340 個の ディールを分析できたのに対して，NT vs Suit では，上のようなディールが 73 個 しかありませんでした。それらを 切り札の枚数と，ボイド，シングルトン，ダブルトンに 従って細分すれば，統計の意味が非常に薄くなります。
統計的分析では，サンプルの大きさが非常に重要です。
(3) ただし，Vernes は，NT での分析の平均誤差が大きくなる原因として， ノートランプ･コントラクトそのものを挙げています。
一般に ノートランプのディクレアラーが取ったトリック数を 一流のプレイヤーについて 統計的に調べると，0.90 トリックの ばらつき があり，スートの場合の 0.52 トリックより大きいことを見つけた，と報告しています。
(4) これらの数値 (0.90, 0.52) を信頼すれば，どんな LoTT 公式も
◇ スートの場合には，ほぼ 1/2 トリック
◇ ノートランプの場合には，ほぼ 1 トリック
の誤差を常に含み，それ以上の細かい議論はあまり意味を持たないことになります。 - それで，結論としては，ノートラの場合，LoTT 公式として [E] を
使えばいいんですね ?
―― いいえ。私の結論は，そうではありません。
- ?? だって，[E] の信頼性が一番高いんでしょう ?
―― はい，それは その通りです。 でも ブリッジのビッドを実践する立場から考えると，それではあまりにも単純すぎる (機械的すぎる)。
私のお勧めは，Cohen 公式 [C] です。これは簡単な形をしています。
それに 7 という数字は 何となく覚えやすい。ノートランプの場合には，これを原点にして考える。 そして，状況に応じて，補正を加える。そのとき，[E] のようなことも 頭の中にチラッっと思い浮かべる (ときには，自信を持って +2 トリックの補正を加える) … それくらいが ちょうどいい。
ブリッジのビッドというのは，何かのシステムや公式に頼って機械的にするものでは ありません (LoTT が普及し始めた頃は，この認識に欠けることがあったように思います)。 Cohen がその著書で強調しているように，LoTT は一つの道具であって，これをうまく 使えるかどうかは，各人の判断 (judgement) にかかっています。主題が LoTT だからと言っても， 判断がキーポイントであることに変わりはありません。 - そういう立場だとすると，スートについての結論は ?
―― 同じように考えます。
基本は LoTT 公式 [A] です。 これは，単純で記憶しやすい。
スートの場合には，これを原点にして考える。 そして，状況に応じて，補正を加えます。そのとき，[B] のようなことも 頭の中にチラッっと思い浮かべる … それくらいが ちょうどいい。 - でも，そうすると，ぼこさんのこれまでの作業が，全部水の泡になってしまう。
―― なってしまうかどうかは，これを読んだ人がどう考えるかに依るでしょうね。
最後に，LoTT が HCP に依らないことを検証します。
この点は，誤解されやすいようで (私自身も，当初は誤解していました)，外国の ホームページやブリッジの本にまで，そのような記述が見られます。
その原因は，LoTT の創始者である Vernes の本を 読み間違える人がいるためでしょう。 Vernes が HCP について言及しているのは,「安全な代の規則」を説明している箇所です。 そこには，この 規則(Règle) の成立要件が 次のように書かれていて
1º les force en honneurs ne doivent pas être réparties trop inégalement entre les deux camps, de préférence entre 17 et 23 points H, à la rigueur entre 15 et 25;
2º la vulnérabilité doit être égale ou favorable. (p.45)
この誤解を解消するには，《統計的検証》が手っ取り早い。そこで，LoTTanalyzer の 中に HCP を制限する機能を付加して，実際に検証してみました。
その結果は簡単明瞭で，LoTT が HCP に依らず成立することは明白です。
Result of  LoTTanalyzer (for suit contracts)
under the Four Requirements for HCP | ||||
| HCP range | 0 − 40 | 15 − 25 | 17 − 23 | 0-14, 26-40 |
| +2 trick deviation | 9.7% | 9.5% | 9.3% | 10.2% |
| +1 trick deviation | 31.5% | 31.5% | 31.5% | 31.0% |
| 0 trick deviation | 38.4% | 38.8% | 39.2% | 37.0% |
| −1 trick deviation | 15.2% | 14.9% | 14.9% | 16.0% |
| Average Deviation | 0.36 tricks | 0.37 tricks | 0.36 tricks | 0.34 tricks |
| Average Error | 0.79 tricks | 0.79 tricks | 0.78 tricks | 0.82 tricks |
| Sample Size | 506,581 | 389,908 | 280,383 | 116,673 |
最右列には，非常に極端な場合として， (15
25 HCP) を除外して，双方の HCP が極端に違う場合を調べました(この機能は，配布されている LoTTanalyzer には ありません)。実際には HCP が
こんなに違うと，競り合いは起こらないはずですが，そういう場合にも，LoTT が
同様に成り立つことが, この表から分かります。
本稿で使用したソフトウェア LoTTanalyzer (および ViewDDLib) は，トップページからダウンロードできます。 直近のバージョンでは，それまで英語対応だったのを，ほぼ全面的に日英両言語対応としました。