


 あなたも LoTTer ?
あなたも LoTTer ?




- 「ロット」の話は,交流ラウンジでも,激しい競り合いの後で,時たま感想に出ることがありますね。
―― はい。どの代まで安全に競り合えるかを判断するときに,
この法則 ( 合計トリック数の法則, the Law of Total Tricks, LoTT ) は,
役に立ちますから …。 - でも,ブリッジのビッドは,覚えることが沢山ありすぎる。
初級者の私も LoTT を理解しなくちゃいけないんでしょうか ?―― これは,ちょっとお答えしにくい質問です。
この法則を普及させた Larry Cohen さんによると (1992),LoTT は基本的な (Fundamental) 概念であって,初心者 (Novice) に対しても絶対に教える必要がある ・・・ と書いています。
現在のビッドのシステムでは,ポイント・カウント法 (A=4, K=3, … と数えるやり方) がビッドを考える上で無くてはならない道具ですが,競り合いの状況では,LoTT がこれと同じような意味で重要になるのです。もちろん,LoTT の発見者である Vernes さん (1966年) も同様のことを言っています。
なので,ぼこもこの頃,交流ラウンジで LoTT という言葉をときどき口にするようになりました。ぼこも "LoTTer" になってしまったのかも知れない。 - ほんとの初心者にも必要なんですか ?
―― いえ,いくらなんでも それはちょっと …。
ポイント・カウント法に頼ってビッドを一通りできるようになることが,何と言っても基本です。それができるようになって,競り合いのビッドに関心を持つようになったら,LoTT の学習を始めればよいと思います。
- それで,その LoTT とは,どういう法則なんですか ?
その法則を知っていると,どういう いいことがあるんですか ?―― それをうまく書けるかと思って書き始めてみたのですが,これがなかなかむずかしい …。
書き始めて,困っているところです。 - そんな無責任な …。
―― 申しわけありません。それで,下に参考になりそうな本とか URI を書き並べて, ごまかそうとしているんだが …。
まだ,LoTT そのものについての説明はうまく書けそうにないのですが,でも,私が LoTT を学習しながら感じたことを 書いてみましょう。
少しは参考になるかも知れないですから。[1] LoTT については,インターネットのあちこちのサイトで短い説明を見ることができます。 私もそういうのを眺めたり,あるいは,下に書いてある「25」の本を 読んだりしました。
そういう短い説明を読んでも,ぜんぜん分かった気がしない。 こういうのは,初めての経験でした。ブリッジのビッドに関することだったら, 書かれていることについて 自分なりに考えれば,それなりに分かるのが普通です。
でも,LoTT ばかりは,そうはいきませんでした。結局,Cohen さんの 2 冊の本を読みました。 それでやっと,おぼろげながら理解できたような感じがして,自分でも少しは使えるかな,という気持ちになりました。
ついでにきちんと調べてみたいと思って,Vernes さんの 1966 年の本もフランスから航空便で取り寄せて読みました。
ほんとのところは,自分がどこまで理解できているのか まだ理解できていないのですが,でも,なんだか奥が深いように思います。
[2] さっきあなたがおっしゃった 2 つのことが重要です。 繰り返すと
(A) LoTT とはどういう法則か.この 2 つです。
(B) LoTT をどう使うか.理屈の上から言えば,(A) をまず理解して, その上に立って (B) 応用する,というのが筋道ですが,どうも そういうふうにスッキリとはいかない。
(A) と (B) の間を おろおろと行ったり来たりしながら,だんだんと理解を深める,というやり方しか無いようです (何を言っているのか全然分からないかも知れないが)。 - じゃぁ,(B) の「使う」という点だけから言うと …。
―― それは (とりあえずは) 簡単です。よく言われるように
という Vernes さんの ルールを使います。(C) You can safely bid to the level equal to the number of trumps held by your side.
味方の切り札の合計枚数に相当する代まで安全にビッドできる。
これを「安全な代のルール (Rule for the Safe Level) 」と呼びます。
後にだんだん説明するように,LoTT がこのルールを保証します。
たとえば,味方がスペードで合計 9 枚の切り札を持っていれば,(競り合いの局面で) 9 トリックまで … すなわち 3 まで安全にビッドできる ・・・ ということです。
まで安全にビッドできる ・・・ ということです。
LoTT の安易な学習法として,(C) を鵜呑みにして実際に使うことをお勧めします。 それで結構うまくいく場合が多いはずです。そしたら,どうしてなのか ? と自分で考えて,本などを読んでみましょう。 うまくいかなかったら,どうしてなのかな ? と考えて,本などを読んでみましょう。無責任な言い方に聞こえるかも 知れないけれど,このやり方が一番良いようです。
でも,結局のところは,(C) だけではだめで,(A) をホントに 理解するところまで行かないと, 真の意味での応用はできません。
さきほど「行ったり来たり」と言ったのは,そういう意味です。私もまだ修行中の身なので,今日のところはこれくらい …。
読んでいただけそうなのが書けたら,ここに載せましょう。 - あっ,ちょっと待って下さい。
「安全にビッドできる」って,どういう意味なんですか ?
スペードが 9 枚あるからといっても,点数が 足りなければ,3 は
ダウンすることだってあるはず …。
は
ダウンすることだってあるはず …。
―― 簡単な例を挙げましょう。
これは,Vernes さんの本 (第 2 章) に載っています。
West の 1 オープンに North が 1
オープンに North が 1 オーバーコールしました。
オーバーコールしました。
このとき,West のハートと North のスペードは,それぞれ何枚でしょうか ?West North East South 1 
1 
3 
3  ?
?
- 5 枚メジャーだから,West のハートは 5 枚以上です。
North は,オーバーコールしたから, スペードを 5 枚以上持っている。―― そうですね。
そこへ,East が 3 をビッドしました。
をビッドしました。
3 は,リミット・レイズとも サイン・オフとも 取れますが,今はそれを問わないことにして,ここで South が 3
は,リミット・レイズとも サイン・オフとも 取れますが,今はそれを問わないことにして,ここで South が 3 をビッドするか / パスするか,というのが問題です。
をビッドするか / パスするか,というのが問題です。
- どう考えるのですか ?
―― もしも競り合いが無ければ (East がパスしていれば),ポイント・カウントを 重視してビッドします。South は,10 pts もあれば,キュービッド 2
 もできるでしょう。
もできるでしょう。
でも,今は East が 3 をビッドして,競り合っています。 W-E 側には,20 pts くらいは あるでしょう。
をビッドして,競り合っています。 W-E 側には,20 pts くらいは あるでしょう。
このような競り合いでは,ポイント・カウントは問題ではなく,切り札の枚数が重要でます。パートナーの 5 枚と自分のスペードの枚数を合わせて,合計 9 枚あれば 3 をビッドします。8 枚以下ならパスします。
をビッドします。8 枚以下ならパスします。
- ずいぶん単純な判断基準なんですね。
ブリッジのビッドは複雑な約束事が多いから,そんなに単純な話を聞くと, びっくりします。―― 私も,最初に これを目にしたときには,本当に驚きました。
その驚きの延長で,これを書いています。
このルール [C] によれば,競り合いの状況では,手の強さを忘れて,切り札の枚数だけで判断します。 - でも,3
 をビッドして,良い手ならメイクするかも知れないけれど,
悪い手ならダウンするはず …。ポイント・カウントを無視して 3
をビッドして,良い手ならメイクするかも知れないけれど,
悪い手ならダウンするはず …。ポイント・カウントを無視して 3 をビッドするというのは,
何だか分かりませんが …。
をビッドするというのは,
何だか分かりませんが …。
―― たしかに,ダウンする場合もあります。
でも,こちらがダウンするのは,相手の手が良い場合です。
そういうときには,相手の方に,もともと 3 とか,あるいは 4
とか,あるいは 4 がある。
がある。
バル / ノンバルにも依りますが,そんなら自分たちで 3 コントラクトを買ってダウンする方が,「損が少ないので得」という考え方です。
コントラクトを買ってダウンする方が,「損が少ないので得」という考え方です。
これが,「安全にビッドできる」という言葉の意味です。
- 北ブリッジ倶楽部のウェブサイト,中級室「トータルトリック」
- Karen Walker さんのウェブサイト (リンク切れ)
初級者のために,LoTT そのものの説明を避け,上のルール [C] に基づく競り合いビッド法を説明しています。
ちなみに,Karen Walker さんは,ACBL の機関誌 "Bridge Bulletin" に寄稿することもあり, そのホームページは 充実しています。 - 山田和彦さんのウェブサイト:"ときには役立つオークション講座"
第 4 回「パーシャル・コントラクトの競り合い」 (リンク切れ) - Barbara Seagram & Marc Smith: "Bridge 25 Ways to Compete in the Bidding" (Master Point Press, 2000) pp.220, $19.95
この本の第 24 章 (pp. 205-212) では,LoTT を要領良く説明しています。練習問題もついています。 - Peter Cheung さんのウェブサイト
LoTT がどのくらいよく成り立つかをコンピュータを使って統計的に調べた結果が見られます。 - Paul Lanier さんのウェブサイト (リンク切れ)
マッチポイントでの LoTT の応用を丁寧に説明する講座 "Law of Total Tricks at Match Points" がありましたが,今はアクセスできません。 - Jean-René Vernes: "Bridge Moderne de la Défense" (L'Édition le Bridgeurs,
第 4 版,1987,初版 1966) pp.195, €11.37
LoTT の発見者である Vernes さんの著書です。(品切れ)
フランス語のハンディキャップもあって,Cohen さんの著書の蔭に隠れがちです。 そこで,その主要部分である第2章全部を,私が 日本語に翻訳しました (2015年7月)。 - Jean-René Vernes: Bridge World,
1969年 6 月に掲載。
上記著書 (第 2 章) の英語抄訳です。(リンク切れ) - Larry Cohen: "To Bid or Not to Bid: The LAW of Total Tricks" (Natco Press, 1992) pp.286, $12.95
LoTT を普及させたベストセラーです。 - Larry Cohen: "Following the Law: The Total Tricks Sequel" (Natco Press, 1994) pp.173, $12.95
Amazon.com の読者書評によると,LoTT を実際にビッドに生かすには,前の本だけでは不十分で,こちらの本も必要だ と書かれています。ていねいに読めば,前の 1 冊だけで十分ですが,こちらも読めば理解が深くなるでしょう。 - Larry Cohen: "Larry and the Law", three articles
in Better Bridge, Vol. 9 (2004/2005), for intermediate players,
#1,
#2,
#3 (PDF).
LoTT の適用について,分かりやすい 3 つの例を示していて,読みやすい。(リンク切れ) 3 篇を一括ダウンロードする. - Colin Ward:
OKbridge Mentoring, Kaleidoscope Series, Lesson 4,「LOTT versus "Got More, Bid More"」
LoTT に基づくビッドの考え方と「強い手では強くビッドする」という従来の考え方を対比させて LoTT を解説しています。 "LOTTer" という言葉は,ここから借用しました。
大変面白い内容ですが,読みづらいので, 組み直しました。⇒ - Matt Ginsberg: "On the Law of Total Tricks" Bridge World (1996 Nov).(リンク切れ)
コンピュータによりダブルダミー解析を行い,LoTT の正しさを裏付けた研究です。 私が HTML 化したファイルを,どうぞ。⇒ - Anders Wirgren: Discussing the Law of Total Tricks
LoTT が破れる場合を詳しく説明しています。したがって,LoTT にどのような問題点があるかを知ることができます。 - Mike Lawrence & Anders Wirgren: "I Fought The Law of Total Tricks" (2004) $17.95. 上のサイトで購入できます。
- おゃ,「続き」を書いていただけるんですか …。
―― はい。
はじめに予定していたことは,あらかた書き終えました (2004 年 1 月) 。
ほんとの初心者の方にもお読みいただけるように,丁寧に書いた積もりです。
でも,そんなに分かりやすい話ではありませんから, ゆっくり読んで下さるよう,はじめにお願いしておきます。 - それでは,そもそも LoTT とは,どういう法則なのですか ?
―― それは,簡単です。
合計トリック数 = 切り札の合計枚数という法則です。
上の例の場合について言うと,仮に
W-E が を合計 8 枚,
を合計 8 枚,
N-S が を合計 9 枚
を合計 9 枚
持っているとすると, 右辺は
切り札の合計枚数 = 8 + 9 = 17
となる。
一方,左辺の「合計トリック数」は,Jean-René Vernes (ジャン-ルネ ヴェルヌ) が 1966 年に考案した全く 新しい概念です。
West-East が を切り札としてプレイをしたときに取れるトリック数と
North-South が
を切り札としてプレイをしたときに取れるトリック数と
North-South が  を切り札としてプレイをしたときに取れるトリック数の和です。
を切り札としてプレイをしたときに取れるトリック数の和です。
「この両辺の数値が等しい」と LoTT は主張します。
このように,合計されたトリック数について成り立つ法則なので,これを,
合計トリック数の法則
(La Loi des Levées Totales,The Law of Total Tricks) ,
略して LoTT と呼びます。上に挙げた著書の中で,Vernes さんがこの法則を提示しました。この法則で重要なのは,あくまでも,トリック数の合計について成り立つ,ということであって, どちらの側が何トリック取れるかについては,何も言っていません。
- 「自分たちが何トリック取れるか」ということと LoTT とは関係無いんですね ?
―― はい,関係ありません。
- 関係ないんだったら,それがビッドと どう関係してくるんですか ?
―― この法則から,どの代まで安全にビッドできるかが分かるのです。
たとえば,上の例について言うと
この場合に,仮に切り札の合計枚数を 17 とすると,合計トリック数が 17 のはずだから,West North East South 1 
1 
3 
3  ?
(A) W-E に 2というのが,この 法則 の教えるところです。
?
(A) W-E に 2というのが,この 法則 の教えるところです。 (8 トリック) しかなければ,N-S の 3
(8 トリック) しかなければ,N-S の 3 (9 トリック) はメイク。
(9 トリック) はメイク。
(B) W-E に 3 しかなければ,N-S は 2
しかなければ,N-S は 2 しかできない。
しかできない。
(C) W-E に 4 があれば,N-S は 1
があれば,N-S は 1 しかできない。
しかできない。
ここで両方ともバルだとして (C) の場合を考えると, 相手側が 4 を作ると −620 点となる。
一方, 3
を作ると −620 点となる。
一方, 3 X で
2 ダウンすると −500 点になる。
X で
2 ダウンすると −500 点になる。
ですから,3 までビッドして,ダブルされても損はありません。
までビッドして,ダブルされても損はありません。
これが,「安全にビッドできる」という表現の意味です。 - もっと分かりやすく比較できないのですか ?
―― 得点と失点の比較を分かりやすくするため,Cohen さんが,チャートと呼ぶ表を考えました。いまの場合には,この表が上のようになります。合計トリック数 17 の場合のチャート 双方ともバル N-S play 3 
W-E play 3 
N-S Tricks N-S 得点 W-E Tricks N-S 得点 (A) 9 +140 8 +100 (B) 8 −100 9 −140 (C) 7 −200 (3  )
)10 −170 (3  )
)
(C') 7 −500 (3  X)
X)10 −620 (4  )
)
- うーんと, …。さっきの説明は (C') の場合ですね。この表の一番下の行にあります。
それでは,3 が 1 ダウンする (B) の場合には …。
が 1 ダウンする (B) の場合には …。
1 ダウンすると,−100点。 それで,もしも 3 をビッドしないと,
をビッドしないと,
W-E の 3 が
ジャストメイクして,−140点。
が
ジャストメイクして,−140点。
結局,どの場合にも (どの行を見ても), 3 をビッドする方が得ということですか.
をビッドする方が得ということですか.
―― はい。その通りです。
LoTT を理解するには,こういうチャートを自分で計算して作ってみることをお勧めします。Cohen さんの 本でも,演習問題になっています。
ただ眺めるだけでなく,実際に自分で表を作ると よく分かります。 - はい。でも …。実際にビッドするときに,こんな表をいちいち作っては いられませんね。
―― それは,もちろん,その通りです。
でも,こんなふうだということが大まかに理解できていれば,実際のビッドには困りません。
話が次へ進む前に,ここで再確認しておきましょう。
味方 (N-S) が合計 9 枚の切り札を持っているとき, 9 トリック (すなわち 3 の代) まで安全にビッドできます。つまり,さっきの「安全な代のルール」が成り立っています。
- それで,その法則は,どのくらい正確に成り立つんでしょうか ?
―― Vernes さんがこの法則を初めて見つけて提唱したときには,沢山のハンドについて自分で調べて,この 法則がよく成り立つことを確かめました。
- 沢山って,どのくらい ?
―― 1953〜1963年の世界選手権戦の公開された ハンドを 2444 個調べたと書かれています。とにかく,1966 年といえば,コンピュータはとても高価で, パソコンなんて無い時代でした。ハンドをひとつひとつ調べるという 根気の要る手作業をなさったようです。
その 2444 個の中で,両方の側が異なるコントラクト (上の例ならば,同じディールを 3 と 3
と 3 ) でプレイした 340 個に
ついて調べてみると,LoTT からのずれが ±1 トリックの範囲に
納まっているのが 272例 (80%) ありました。
) でプレイした 340 個に
ついて調べてみると,LoTT からのずれが ±1 トリックの範囲に
納まっているのが 272例 (80%) ありました。
すなわち,1 トリックの誤差を許容すれば,80% の場合について LoTT は 成り立ちます。
また,誤差の (絶対値の) 平均は 0.93 トリックでした。 - 1 トリックの誤差は,大きなようにも見えますが …。
―― 1 トリックをどの程度の大きさと見るかは,人によって違うでしょうね。
これを何かと比較する必要があります。
Vernes さんは,これをプレイヤーの腕のばらつきと比較しました。
世界選手権級の上手なプレイヤーが 同一のハンドを同一のコントラクトでプレイした結果を比較すると,平均して 0.52 トリックの ばらつきが ありました。
したがって,1 トリックの誤差は有意 (significant) です。 - 「有意」って … ?
―― あぁ,それは統計で使う用語です。この場合だったら,
「 1 トリックの差は,無視できない誤差である」
という意味です。
つまり,LoTT は,いつでも厳密に成り立つのではなくて,1 トリック程度の誤差が あると思わなければいけない … ということです。
Vernes さんが 340 個のハンドについて調べた結果は,次の通りです。
(1) LoTT は,27.6% の場合に +1 トリックだけずれる (過少評価する)。
(2) LoTT は,33.2% の場合に正しい (的中する)。
(3) LoTT は,19.1% の場合に −1 トリックだけずれる (過大評価する)。
(4) ずれの平均値は +0.275 トリックである。
(5) 平均誤差は 0.93 トリックである。
〔 誤差 = |ずれ| (すなわち,"ずれ" の絶対値) が Vernes さんの定義です〕
このように,約 1 トリックの誤差を避けられない法則なので,Vernes さんは
"合計トリック数は,
切り札の合計枚数に近似的に等しい (approximativemant égal)"
と表現しました。
ところが,Cohen さんの受け止め方は これとは違っていて
"合計トリック数は,
どんなハンドでも切り札の合計枚数に等しい (on any deal equal)"
と表現しました。Cohen さんは,自分の経験から,LoTT が非常によく成り立つと考えたのでしょう。
その後,Wirgren さんは,上記の "どんなハンドでも" という部分,すなわち, "近似的に" を 切り捨てたことに鋭い批判を加えました。
そのためかどうか分かりませんが,Cohen さんの 2 冊目の本には,
"近似的に (approximately)" が 追加されました。
- そもそも,なぜ,そういう法則が成り立つのですか ?
―― そぅそぅ。LoTT の議論では,そこが一番のポイントです。
「なぜ,LoTT が成り立つか ? 」
あるいは
「どういう前提の下で,LoTT は成り立つか ? 」
ところが,Vernes さんの本には,そういう説明が無いのです。 - えっ ? 全然無いんですか ? 説明が …。
―― びっくりなさるかも知れませんが,そういう理論的な説明は全く書かれていません。
「実際に成り立っていることを 統計データに基づいて検証する」のが重要という考えのようです。 理論的な説明を何か考えているはずだと思って,フランス語の著書をわざわざ (航空便で €31.37) 買って読んだのですが,期待外れでした。
まぁ,法則というのは,定理とは違って,証明を必要としない。 だから,よく成り立っていればそれでいいのですが …。そういうわけで,ここは,自分で考えるしかありません。
Cohen さんの本にも, 理路整然とした説明は全く書かれていないのですが ( これにもがっかり ) , でも,ノートランプの場合の説明 (第7章) から敷衍すると, LoTT が成り立つ理由を,次のように説明できそうです。[a] 議論の出発点を固めるために,切り札無しの場合から始めます。
ノートランプ・コントラクトです。
その場合,カードがほぼ均等に配られていると仮定すると, どちらかが 7 トリックを,他方が 6 トリックを取る。この場合の合計トリック数は,もちろん 13 です。[b] 次に,( やはり,カードがほぼ均等に配られているとして ) スート・コントラクトを考えます。 カードの分布がすべてのプレイヤーについて 4-3-3-3 のバランス・ハンドで, HCP が均等に分かれているとします。
この場合, どちらの側も,切り札の枚数は 7 枚です。したがって,
切り札の合計枚数 = 7 + 7 = 14
です。
次に,取れるトリック数のほうを考えると,どちらの側がコントラクトを勝ち取ったとしても, 余分の ( 刈り上げに使った後に残る ) 切り札 1 枚をラフに使えるので,手の強さが均等ならば, どちらがコントラクトを勝ち取っても 7 トリックを取れます。したがって,
合計トリック数 = 7 + 7 = 14
となります。この場合,LoTT は確かに成立します。[c] ここで,切り札の枚数分布だけは固定して,カードを入れ替えます。
切り札の枚数が同じなら,どういう入れ替えでも構いません。
カードを入れ替えると,どちらかが取れるトリック数が増えます。
でも,その分だけ相手側の取れるトリック数が 減ります。したがって,合計トリック数が 14 であることに変わりはありません。
ここが,LoTT の一つのポイントです。カードを入れ替えると,取れるトリック数は それぞれ変化しますが,でも,合計のトリック数は不変なのです。
現実には,この不変性はいつでも保たれるとは限らず,例外があります。
しかし,LoTT は,この ( カード交換に対する合計トリック数の ) 不変性を 基礎として成立します。[d] ここから更にカード交換を行い,切り札の枚数を変更します。
切り札を 1 枚ふやすと,ふえた切り札はラフに使えるので,取れるトリック数が 1 だけふえます。 つまり,LoTT は,7 枚目以降の切り札がすべてラフに使えることを前提として成立します。
ここに,LoTT の第 2 の特徴が現れています。切り札の枚数が重要だということです。[e] さらに一つ付け加えると,ここでは,ラフで取れる/取られるトリックを除いて, カードの取れ方は, 「攻め」に回っても「受け」に回っても同じだと考えています。つまり,ディクレアラーの立場で勝てるカードは, 同じプレイヤーがディフェンスに回っても,同じように勝てると仮定しています。
たとえば,ディクレアラーがフィネスで取れるカードは,ディフェンスに回っても同じようにフィネスで取れます。 - 上の説明は,ぼこさんが考えた説明なのですか ?
―― はい,そうです。どこかで誰かが上のようなことを書いてあるはずだと思うのですが, ひとつも見たことがありません。 LoTT に厳しい目を向けている Wirgren さんも,LoTT が成り立つ理由をきちんと書いたものは無いと言っています。 そして,さらに,理論的な説明ができないのだから,合計トリック数と切り札の合計枚数とは無関係である ( There is no connection. ) とまで主張しています。
- ぼこさんは,どう考えているのですか ?
―― 私は,いまのところ,次のように考えています。
LoTT は, 1 トリックの誤差を許容すれば,かなりよく成り立ちます。
ですから,LoTT が成り立つ大まかな理由を ひとまず上のように考えて理解しましょう。成り立つ理由を理解できれば, どういう場合に成り立たないかも理解できるはずです。
現実にある程度よく成り立っている法則なのですから,なぜ成り立つのかを考えることから, 議論が始まるはずだと思います。
- 「法則」というけれど,いつでも厳密に成り立つ法則ではないのですね ?
―― たしかに,数学の定理や物理の法則とは違います。
「例外なく成り立つ法則」ではありません。
法則からずれる場合もある。
実際に使うには,どういうときにどうずれるか,も重要です。
この「ずれ」を 予測して折り込むことを,Vernes さんは 補正 (corrections) と呼び,Cohen さんは 調整 (adjustments) と呼んでいます。 - どういうときにどうずれる,ということがあるのですか ?
―― はい。
- どんな … ?
―― それがちょっと単純な話ではありません。Cohen さんが 2 冊目の本を書いた理由の一つが, それをきちんと説明して,LoTT を使いやすくしたかったからです。
いくつかの要因があります。[1] はっきりしているのは,ダブル・フィットがある場合です。 この場合には,プラスにずれます ( 合計トリック数を過少評価します ) 。
Vernes さんによれば,これは最大の要因であり,1 トリックくらいの過少見積もりになります。 一方,Cohen さんによると,これは,2 番目の要因です。
上の説明から分かるように,サイド・スートについて,LoTT では,HCP の大小により カードの勝ち負けが自然に決まると考えています。
「長さ」で勝つことは,考慮に入っていません。 このため,切り札以外にも長いスートがあると,合計トリック数が切り札の合計枚数より多くなります。ただし,ダブル・フィットについて,Vernes さんは「双方に 8 枚以上のダブル・フィットがあるときに +1 トリック と考える」と言っています。
すなわち,2 重のダブル・フィットがある場合です。 Cohen さんもこれに追随して,Vernes さんの著書の当該部分をなぜか引用せずに,「2 重」を強調しています。
実は,ここで「2 重」ということを ことさらに強調する必要はありません。 なぜなら,「1 重」のダブル・フィットは存在しないからです。
後の方の確率の計算で分かるように,片方に 8 枚のダブル・フィットがあるときには,他方の側には 必ず 9 枚以上のフィット または 8 枚のダブル・フィットがあります。[2] ディフェンス向きのカードは,マイナスの要因になります。
たとえば,相手方の強いスートに (切り札でも サイド・スートでも) Q J x とか Q x x を 持っているとき,この Q は,防ぎには利きますが,攻めには利かないので ( x x x でも, 3 枚目をラフできるので) ,合計トリック数を減らす要因になります (後のハンド例を参照して下さい)。 私は,このようなカードをカメレオンと呼んでいます。立場によって,勝ち負けが変わるからです。
Cohen さんは,これを補正の第 1 要因としています。
一方,Vernes さんはこれを補正の第 2 要因に挙げて,その重要性は,普通に思うより遥かに小さいと述べています (原文)。[3] 切り札の枚数が 10 枚とか 11 枚のような場合に,ただそれだけで単純に喜ぶのは危険です。 いくら二人で切り札を沢山持っていても,サイド・スートが止まらないと, 相手側が頭からサイド・スートの勝ち札を取ってしまうので,切り札が有効に使えません。
LoTT は 切り札で切れることを前提にしているので,切り札が多い場合には, ボイドやシングルトンが無ければ, 合計トリック数は予測より少なくなります。つまり,ハンドの形 (カードの枚数分布) が 重要です。この点は,上に述べた「理由」から よく理解できます。
このようなハンドの実例は,私のソフトウェア LottAnalyzer と ViewDDLib を組み合わせると, 沢山見られます。 合計トリック数が 20 を越えると,LoTT が過大評価することを具体的に理解できます。[4] これ以外に考えられる補正としては,「逆ラフ」があります。
逆ラフ (Adverse Ruff) とは,ディフェンダ側が ラフによりトリックを勝ち取ることです。逆ラフは,ディフェンダの持っている切り札が弱くて少ない場合にも 起こり得ます。これが起きると,当然,合計トリック数は減ります。
もともと LoTT では,ディクレアラーが切り札を使ってラフにより多くのトリックを取るものと想定しており (逆刈りは,想定の範囲内ですが), 逆ラフは 想定外です。 実戦家である Cohen さんも 逆ラフには当然気づいているはず (そういう例が本には載っている) なのに, この補正には全く触れていません。オークションの最中に 逆ラフを予測することが 不可能だからでしょう。[5] LoTT からのずれについては, Wirgren さんの研究があります。
詳しくは,上のリファレンスを参照して下さい。これによると,Cohen さんの本の中の説明以外にも,いろいろの要因があることが分かります。
一つの重要な要因は,サイド・スートのコントロールです。たとえば,強くて長いでも,そのためには, と弱い
と弱い  がサイド・スートの場合,
がサイド・スートの場合, を使って
を使って  の負け札を消そうとします。
の負け札を消そうとします。
 のコントロールが必要です。ディクレアラーが
のコントロールが必要です。ディクレアラーが  Kxx を持っていれば,
Kxx を持っていれば, の負け札は 1 トリックで済みます。けれども,ダミーが
の負け札は 1 トリックで済みます。けれども,ダミーが  Kxx を持っていたのでは,
Kxx を持っていたのでは, を全部取られることもあり得ます。つまり,どちらがディクレアラーになるかによって,取れるトリック数に差が出ます。こういうことは,LoTT では全く考慮されていません。
を全部取られることもあり得ます。つまり,どちらがディクレアラーになるかによって,取れるトリック数に差が出ます。こういうことは,LoTT では全く考慮されていません。
[6] Cohen さんがその 2 冊の著書で強調しているのは,「ハンドの純粋さ (Purity) 」によるプラスの調整です。 向かい合った味方同士のハンドを合わせて, ひとつの長いスートに A K Q J がそろっているようなハンドは「純粋 (Pure)」であって,沢山のトリックを取れます。 Cohen さんは,これを第 1 の補正要因と主張します。
けれども,ふたりのハンドが Pure であるかどうかは,ハンドを開いてみて初めて分かることです。 ビッドの段階で分かるのは,カードの枚数だけなので,このような基準は "To Bid or Not To Bid" には 役に立ちません。ひょっとして,Vernes さんとの違いを強調するために,これを先頭に置いたのかも 知れませんが,少なくとも,頻繁に発生する補正要因ではありません。
1996年, ブリッジ・ソフトウェア GIB (Ginsberg Intelligent Bridge Player) で その名も高い Matthew Ginsberg さんは,自慢のダブルダミー分析器を用いて LoTT がどのくらい よく成り立つかを調べ,その結果を Bridge World (1996 Nov) に "On the Law of Total Tricks" と 題して公表しました。この論文は,上記リファレンスから入手できます。
446,741 個のディールから得られた主な結果は,次の通りです。
(1) LoTT は,22.4% の場合に +1 トリックだけずれる (過少評価する)。
(2) LoTT は,40.0% の場合に正しい (的中する)。
(3) LoTT は,24.5% の場合に −1 トリックだけずれる (過大評価する)。
(4) すれの平均値は,−0.05 トリックである。
(5) 平均誤差は,0.75 トリックである。
そして,結論として,次のように述べています。
provided that the trump lengths combine to 20 cards or fewer, the Law of Total Tricks will lead you to correct decisions approximately 70% of the time.
ただし,仔細に見ると,違いがあります。
平均誤差は,それぞれ 0.93 トリック (Vernes), 0.75 トリック (Ginsberg) です。 後者の方がサンプル数が圧倒的に多いので,ばらつきが小さいことは理解できます。
一方,ずれの平均値は,
+0.275 トリック (Vernes),−0.05 トリック (Ginsberg) です。
すなわち,Vernes さんの結果によれば,LoTT は合計トリック数を過少評価するので, 平均としては,プラスの補正が必要です。
けれども,Ginsberg さんの結果によれば,補正の平均はほぼ 0 です。
両者の違いについて私が考えたことを,本稿の末尾に記載します。
- 片方の側がノートランプの場合,LoTT はどうなるのですか ?
―― スート・コントラクトと NT コントラクトが競り合う場合ですね …。
その場合の説明は,Cohen さんの 1 冊目の本 (第 7 章) に書かれています。 結論は,こうです。合計トリック数 = 切り札の枚数 + 7 - なぜ,そうなるのですか ?
―― もともと NT コントラクトの場合には,どちらの側が ノートランプのディクレアラーになったと しても,合計トリック数は 13 です。
ここでは,強いカードが HCP によって勝つことを想定しています。
長さにより勝つことは,想定していません。
そこで 片方が切り札を持ってプレイすると, 切り札のある側は,前の説明から分かるように, 7 枚目 以降の切り札をラフに使います。 その結果,合計トリック数は
13 + ( 切り札の枚数 − 6 )
となります。これが,上の公式です。(注) Vernes さんの公式は,上と少し違い,
合計トリック数 = 切り札の枚数 + 8, 7, 6です。右辺の 3 個の数字は,スート・コントラクト側の最も短い サイド・スートの 長さによって
ボイドのとき 8, シングルトンのとき 7, ダブルトンのとき 6
とします。
つまり,シングルトンがあるとき,両公式は一致します。
ここで,サイド・スートの長さは,ディクレアラー,ダミーを問いません。すなわち, ディクレアラーがシングルトンを持つ場合でも,ダミーがシングルトンを持つ場合と同様に,+7 と 数えます。この点は,Vernes さんの慧眼と言えるでしょう。ところが,最近の私の統計分析によると,Vernes 公式に 1 を加えた
合計トリック数 = 切り札の枚数 + 9, 8, 7これが最もよく成り立つことが分かりました。この公式は,ダブルトンの場合に Cohen 公式に一致します。これについては,本稿の末尾で触れます。 - この場合にも,「補正」は ?
―― 長いスートが LoTT では考慮されていない,という点は,NT でも同じです。
NT コントラクトは,必要最小限のストッパと長いスートでメイクすることがよくありますが, その場合には,合計トリック数に対して,プラスの補正を考える必要があります。 - 上の Cohen さんの公式で,ボイドやシングルトンは,どう補正するのですか ?
―― 上の本は,ボイドに +1 トリック,シングルトンに +½ トリックを与えています。ビッド例も載っています。
- ぼこさんの公式は,それより大きな補正をするんですね ?
―― はい。補正の理由を自分なりに考えて,+1, +½ ではなしに,+2, +1 と 補正するのが良いと思うようになりました。そして,統計的結論がこれを支持することが分かりました。
- NT のコントラクトと競り合うとき,上の法則をどんなふうに使うのですか ?
―― 片方が NT を目指すと,状況は かなり変わります。
荒れたハンドで,双方が 4 とか 5 の代の スート・コントラクトを激しく競り合うような場合には, 合計トリック数が 20 以上ということもあります。
けれども,片方が NT の場合には, 上の式から分かるように,合計トリック数がそんなに大きくなりません。 せいぜい 2 とか 3 の代の競り合いになります。つまり,合計トリック数が,もともと少ないのです。 - 話を具体的にして,1NT オープンに対して競り合う場合には ?
―― 1NT オープンに対して,もしも合計 8 枚の切り札を持っていれば,
上の式から
合計トリック数 = 7 + 8 = 15
となるので,2 の代で安全に競り合うことができます。 - 合計トリック数 15 という数字から,なぜ 2 の代で安全に競り合える と言えるのですか ?
―― LoTT に頼って正確な議論をするためには,いつでも,「チャート」と呼ばれる表を作って,得点と失点を比較検討します。
合計トリック数が 15 の場合のチャートは Cohen さんの本には載っていないので,自分で作ってみると,下のようになります.合計トリック数 15 の場合のチャート 双方とも ノンバル We play in 2 
They play in 1NT Our Tricks Our Score Their Tricks Our Score 9 +140 6 +50 8 +110 7 −90 7 −50 8 −120 6 −100 9 −150 - この表の読み方は ?
―― 相手の 1NT にあなたが 2
 オーバーコールしました。
オーバーコールしました。
 は,あなたの側に 8 枚あります。
は,あなたの側に 8 枚あります。
このとき,合計トリック数は,相手方のカードとは無関係に,15 です。
この場合の得点と失点が,このチャートのようになります。
2 がジャストメイクすれば +110 点です。
この場合,もしも 2
がジャストメイクすれば +110 点です。
この場合,もしも 2 を
ビッドしなければ,相手方の 1NT がジャストメイクするので,−90 点となります。
を
ビッドしなければ,相手方の 1NT がジャストメイクするので,−90 点となります。
- でも,2
 がダウンすることも ありますね。
がダウンすることも ありますね。
―― はい。もしも 1 ダウン なら −50 点 (ダブルがかかって 1 ダウンなら −100 点) です。
でも,2 をビッドせずに相手に 1NT を取らせると 2 メイクして,−120 点 …。
をビッドせずに相手に 1NT を取らせると 2 メイクして,−120 点 …。
これが,LoTT から言えることです。つまり,ダブルを掛けられてダウンするとしても,ノンバルならば 2 をビッドする方が
得です。
をビッドする方が
得です。 - じゃぁ,2
 が 2 ダウンする場合には ?
が 2 ダウンする場合には ?
―― その場合には,話は簡単です。
2 が 2 ダウンすると,この表から分かるように,−100 点。
もしも ダブルが掛かって 2 ダウンなら −300 点。
が 2 ダウンすると,この表から分かるように,−100 点。
もしも ダブルが掛かって 2 ダウンなら −300 点。 - ずいぶん大きな損ですね。
―― 一見 そう見えますが,2
 が 6 トリックしか取れなくて, 2 ダウンするなら,LoTT により
が 6 トリックしか取れなくて, 2 ダウンするなら,LoTT により
15 − 6 = 9
つまり,相手は 9 トリックを取って,3NT がメイクするはずです。
3NT をメイクすれば,相手は 400 点。
だから,2 ダウンの −300 点でも, こちらは大成功です。 - なるほど …,切り札がこちらに 8 枚あるならば … ですね。
―― はい。
- LoTT を使う考え方は,よく分かりました。
デュプリケートのブリッジだから,仮に失点があったとしても, 「失点が少なければ得」ということなんですね。―― はい。その通りです。
それが「安全にビッドできる」という表現の意味です。
そして,この場合にも,「安全な代のルール」は成立しています。
8 枚の切り札で 8 トリック ( 2 の代 ) まで安全にビッドできます。 - 考え方は分かりました。でも,実際のビッドは ?
私ひとりでハートが 8 枚なんてことは ほとんどありえませんから …。―― はい,その通りです。
実際には,6 枚のしっかりしたスートがあれば, 1NT に対して,2 の代でオーバーコールします。 残りの 7 枚の分布は分かりませんが,そのうちの 2 枚をパートナーに期待します。
正確な確率計算によると,あなたが 6 枚持っているスートに パートナーが 2 枚以上を持つ確率は,76.3 % です。 つまり,ほぼ 4 回中 3 回の割合で,この期待が当たります ( リンク先の 表の「自分の枚数」= 6 の行を見ましょう )。
- ここまでで,「安全な代のルール」
味方の切り札の合計枚数に相当する代まで安全にビッドできる。というのが役に立つことが分かりました。
その説明では,「チャート (#1, #2) 」というのを使って確認しました。
ここで分からないのは,LoTT と上のルールのあいだの関係です。
このルールは,LoTT を使って「証明」できるのですか ?―― 大上段に証明することは できません。
もともと,このルールは,Vernes さんが LoTT を前提として経験的に発見しました。 つまり,上で 2 つの例についてチャートで確認したのと同様に, いろんな代のいろんな競り合いについて沢山調べました。その結果として, 上のルールが成り立つことを見出したのです。そして,このルールについて,次の 3 条件を挙げています。以上の 3 つです。ただし,これらの条件は,Cohen さんの本では完全に無視されてしまったので,条件を未だ知らずにルールを使っている人は多いでしょう。- このルールは,スモール・スラムまでの全ての代で成り立つ。
- このルールが成り立つためには,両者の手の強さが余りにも不均衡であってはならない。
できることなら (de préférence) 17〜23 HCP のあいだ,
いざという時には (à la rigueur) 15〜25 HCP のあいだ。 - バルネラビリティーは有利または同等の状況でなければならない。 不利な (味方がバルで,相手がノンバルの) 状況では, 味方の HCP が相手と同等 (または ほゞ同等) でなければならない。 (原文)
- ということは
( ルールが LoTT を前提にしているのだったら ) …。
LoTT と上のルールとは同じものだと 考えてよいのですか ? ―― まぁ,そう考えても大きな間違いはありません。実際に役に立つのは, LoTT そのもの よりも,「安全な代」を知ることなので,同じと思っている人が多いように見受けられます。LoTT を 定理 (Theorem) とするなら,このルールは,定理の系 (Corollary) です.ただし,両者は別物です。これを明確に認識するには,次の 2 点を指摘すれば 十分です。
(理系の人には,この言い方が分かりやすい)(1) LoTT は,バル / ノンバルとは無関係に成立する。実際のビッドでは,上の 3 条件が言うように,バルネラビリティも HCP も考慮する必要があります。
(2) LoTT は,双方の HCP とは無関係に成立する (下記参照)。 - 上のルールは,LoTT に基づいて Larry Cohen さんが考えたのかと思っていましたが …。
―― よくそう誤解する人がいます。でも,そうではありません。
上のルールも Vernes さんが LoTT と同時に提唱しました。
Vernes さん自身は,このルールを "la Règle de Sept à Douze" と名づけました。
英語にすると, "Rule of Seven to Twelve" です。 つまり,スモール・スラムの代までの競り合いに有効なルールだという意味です。でも,非常によく使われているルールの割りには,締まりの無い (失礼!) 名前なので,この名前は使われずに,名無しさんのままになっています。
英語では,"Rule of Security","Law Protection","Distributional Security (Sécurité Distributionelle)",あるいは もっと締まりのない "LAW's Competitive Guideline" などが使われています。
「安全な代のルール (Rule for the Safe Level) 」は,私の命名ですが,分かりやすいと思います。 - スモール・スラムと HCP の範囲とは重なっていないように見えますが …。
―― そうですね。そこは疑問に思っています。ここでは,書かれていることをそのまま紹介しました。 後は,自分で考えるしかありません。
ほんとは,Vernes さんが,自分の考えをもっとはっきりと (主観的でもいいから) 説明してくれると面白かったのですが …。
この人は,統計学に関心があるらしくて, ブリッジ統計学者と呼ぶのがいいのかも知れません。とにかく,データに基づいて主張できることだけを,主観をまじえずに 書いていますから。でも,だからこそ,LoTT の信頼性が高いんでしょうね。
- さっき ちょっと言いそびれたことが …。
―― どんなことですか ?
- [ルールの条件] ひとつ前の節で,「安全な代のルール」には,3 つの条件があるということでした。
条件 A と条件 C は,このルールを使うときに,たぶん必要なのでしょう。
問題は,HCP に関する条件 B です。
この条件 B は,
[1] もともと LoTT の成立条件として必要だ.
[2] LoTT とは無関係であって,このルールのために必要だ.
この 2 つのうちの どちらが正しいのでしょうか ?―― うむ,これは鋭い質問です。
実は,私も はじめのうちは,その区別がつかず,ごっちゃにしていました.
正解は,[2] LoTT と HCP とは無関係に成り立つ, です。 断言します。 - [断言の理由] どうして そう断言できるのですか ?
―― 詳しいことは,ハンドの例を挙げて考える必要があります。
でも,ここでは,2 つの証拠を提示しましょう。
1 つの証拠は,コンピュータを使ったダブルダミー解析です。
そのために,私はLoTTanalyzer という ソフトウェア を作成しました。
これを使って,(Matthew Ginsberg さんが用意して下さった) 717,102 個のディールについて調べた結果は,次の通りです。
約 50万個のディールについて得られた結果です。LoTTanalyzer により得られた結果 (NT を除く)
HCP の範囲 0〜40 HCP 15〜25 HCP 17〜23 HCP +2 トリックの外れ 9.7% 9.5% 9.3% +1 トリックの外れ 31.5% 31.5% 31.5% 0 トリック,的中 38.4% 38.8% 39.2% −1 トリックの外れ 15.2% 14.9% 14.9% 外れの平均値 0.36 トリック 0.37 トリック 0.36 トリック 平均誤差 0.79 トリック 0.79 トリック 0.78 トリック ディール個数 506,581 389,908 280,383
ごらんのように,HCP を無制限にしても (0〜40),2 通りに制限しても, LoTT の成立状況は,全く同じです。とくに注目すべきは,「ばらつき (平均誤差)」が等しいことです。
すなわち,LoTT は HCP と無関係です。
これは,明確な証拠です。
- 2 番目の証拠は ?
―― これは,「証拠」とは呼べないかも知れませんが,Vernes さんという人は, 言葉を選んで注意深く 本を書いています。
LoTT の説明のところでは,HCP などという言葉は現れません。
上の条件のところで,初めて HCP が登場します。
この書き方から,LoTT と HCP を無関係と考えていることは明白です。
もしも,何か関係有りと思っているのでしたら (Vernes さんの ことですから,そういう データ を持っていれば),そう書いたはずです。 - ぼこさん,入れこんでますね。 …かなり。
―― そうかも知れない。でも,ほんとに偉い人だと思います。
だって,(1) 何の役に立つのか分からない「合計トリック数」なんていう奇想天外な概念を思いつき,(2) LoTT を発見し, さらに (3) それをルールに定着させる ――
これを 1966 年までに独力で なさったのですから。 - それでは,3 番目の証拠は ?
―― それは,困りますね (笑)。
条件 B は,あまりにも無理な競り合いを戒める意味です。
このルールだけに頼った場合,切り札がたくさんあると,それだけの理由で高い代まで競り合います。 でも,手の強さが不足していれば,損することがある。それを戒めるのが,条件 B です。
LoTT そのものは成り立っていますが,相手方が取るトリックがずっと多くて, 味方がそれほどトリックを取れないと,こういう羽目に陥ります。North 双方とも バル  A 4
A 4
 K 8 6
K 8 6
 J 8 5 3
J 8 5 3
West  K 9 8 3
K 9 8 3
East  K Q J 8 7 5 3
K Q J 8 7 5 3
 10 9 6 2
10 9 6 2
 J 9
J 9
 Q 7 4
Q 7 4
 Q 9 6
Q 9 6
 10 4
10 4
 6
6
 J 10 4 2
J 10 4 2
 —
—
 A 10 5 3 2
A 10 5 3 2
 A K 7 2
A K 7 2
 A Q 7 5
A Q 7 5
South 右の場合を調べましょう。
まずは,切り札の枚数から。 - W-E は,スペード 11 枚。
N-S は,ハート 8 枚。
切り札の合計枚数
= 11 + 8 = 19.―― その次は,それぞれ何トリック取れるか。
- W-E は,7 トリック (ちょっと少ない,目算外れ)。
一方,N-S は, と
と  に
負け札が 1 枚ずつあるので,11 トリック。
に
負け札が 1 枚ずつあるので,11 トリック。
したがって,合計トリック数 = 7 + 11 = 18.―― この場合,LoTT は 1 トリックの過大評価ですが,まぁほぼ成り立っていると言えるでしょう。 少なくとも,狂ってはいません。
ここで,N-S の 5 に対して,W-E が 5
に対して,W-E が 5 をビッドするかどうか …。
をビッドするかどうか …。
- もしもパスして,5
 をメイクされると,5×30 + 300 = 450 点。
をメイクされると,5×30 + 300 = 450 点。
でも,11 枚持っているから,「安全な ( はずの ) 代のルール」が守ってくれるはず …,だから 5 をビッド。
そこへ もちろんダブルが掛かって …。
をビッド。
そこへ もちろんダブルが掛かって …。
その結果は 11 − 7 = 4 ダウン。 −800 点 !―― ここで,双方の HCP を数えてみると,12 HCP と 28 HCP.
これは,Vernes さんが指摘する危険水域です。
本来ならば,安全な代のルールを使うべきなのに,「安全なはずの代のルール」を使ってしまった例です。 - なるほど。この例は,よく分かります。
強さが不足していれば,ルールを使っても無意味ですね。―― 話の続き具合がよいので,合計トリック数の推定に 話を進めましょう。 というのは,このようにハンドが開いていれば,切り札の枚数が分かりますが,実際に ビッドしているとき,合計枚数が何枚かは,推測するしかありません。
- そうですね。それは,どんなふうに …。
―― W-E と N-S の立場になって,それぞれ考えてみましょう。
W-E の方が (一見すると) 簡単です。West はジャンプして 3 をビッドします。
をビッドします。
それを聞いた East は,切り札が 11 枚あることを知ります。 かなり荒れたハンドなので,合計 11 × 2 = 22 トリックくらい あるかも ?,そしたら,5 までビッドしても
「安全な代のルール」が 守ってくれる … てなふうに考えるでしょう。
までビッドしても
「安全な代のルール」が 守ってくれる … てなふうに考えるでしょう。
- はい。
―― 一方,N-S は,8 枚の切り札を持っています。 ダブル・フィットなので,9 枚と数えると, 2 × 9 = 18 トリックくらいはありそうか …
そこへ West が 3 をビッドすると,
相手の枚数が 9 枚以上だと分かるので,合計トリック数を 19 〜20 に嵩上げして考えます。
をビッドすると,
相手の枚数が 9 枚以上だと分かるので,合計トリック数を 19 〜20 に嵩上げして考えます。
N-S の方は良い手なので,このように考えて問題無いのですが,
W-E は,上の段階で落し穴に 嵌まっているのです。 - たぶん,そうなのでしょうね。 11 トリックのはずが,7 トリックしか取れないのですから。
でも,どういう落し穴なんですか ? 嵌まらないための注意は ?
North 双方  A 4
A 4
ノンバル  K 8 6
K 8 6
 J 8 5 3
J 8 5 3
West  K 9 8 3
K 9 8 3
East  K Q J 8 7 5 3
K Q J 8 7 5 3
 10 9 6 2
10 9 6 2
 J 9
J 9
 Q 7 4
Q 7 4
 Q 9 6
Q 9 6
 10 4
10 4
 6
6
 J 10 4 2
J 10 4 2
 —
—
 A 10 5 3 2
A 10 5 3 2
 A K 7 2
A K 7 2
 A Q 7 5
A Q 7 5
South ―― 見やすいように,ハンドを再掲します。 4 つの手を開いて見れば分かるように,West の
 Q と East の
Q と East の  Q には
特徴があります。分かりますか ?
Q には
特徴があります。分かりますか ?
- どんな特徴が …。あっ !
そうか。 この 2 枚は,どちらも相手のコントラクト 5 では勝っている。
では勝っている。
でも,自分たちの 5 では,トリックを取っていない。
では,トリックを取っていない。
 Q は 2 回のフィネスで勝てる。
でも,これは屑札でもいい。ダミーでラフできるから …。
Q は 2 回のフィネスで勝てる。
でも,これは屑札でもいい。ダミーでラフできるから …。
―― その通りです。
このように立場が変ったときに勝ち負けが変化する ( カメレオンのような ) カードには,要注意です。 これらのカードは,合計トリック数を 下げる はたらきを持ちます。 ですから,単純に 22 トリックと数えるのは まちがいで, 22 − 2 = 20 トリックくらいと考える。そうすれば,5 をビッドするのは,
ちょっと危険かな … と。
をビッドするのは,
ちょっと危険かな … と。
East の判断材料としては,こんなに高い代の競り合いで シングルトンが無い,というのも危険の兆候です。 - 一般には,どういうカードが カメレオン なんですか ?
―― 上の例から分かるように,相手の強いスート (切り札を含む) に, Q x x がある場合です。もしも, 相手の切り札に Q J x を持っていれば,絶対に カメレオン。
こういうカードは,防ぎには有効です。しかし,攻めに回ったとき,カメレオンは,自分からトリックを 取るパワーがありません。〔パートナーはこのスートが短いので,3 枚目をラフできます〕。 そういうカードを持っているときには,合計トリック数を抑え目に評価します。
その場合,チャートを使った議論から明らかなように,「安全な代」は 当然 下がります。
- ところで,LoTT を上手に使うためには,ビッドの状況から切り札の枚数を判断する必要がありますね。
―― はい。あります。それは,とても重要です。
- それは,どうやって …。
―― 普通のビッドができれば,かなりの程度は分かるはずです。
上に引用したウェブサイトなどでも説明されています。
大事なことなので,Cohen さんの 2 冊の本でも,その極意が詳しく説明されています。
重複して書くのは意味が無いので,それについては省略したいのですが,基本的には,切り札の枚数が はっきり分かるようにビッドすることが重要です。 - どういうことですか ? …
―― たとえば,オークションが
と進んだ場合を考えましょう。West North East South 1 
1 
2 
2 
3 
?
このとき,North が 3 をビッド
するか / パスするか
という問題です。
をビッド
するか / パスするか
という問題です。 - どう考えるのですか ?
―― ポイント・カウント法に基づいて普通にビッドする場合には,
良い手なら 3 をビッドする
をビッドする
ことになるでしょう。
しかし,パートナーとのあいだで LoTT を重視する取り決めをしている場合には,ポイント・カウントを無視して, スペードの枚数だけで判断します。
North は,オーバーコール 1 で 5 枚以上のスペードを
保証しています。
South のサポート2
で 5 枚以上のスペードを
保証しています。
South のサポート2 は,3 枚以上を保証しています。
は,3 枚以上を保証しています。
そこで,North はスペードが 5 枚ならば パスを,コールします。
スペードが 6 枚ならば 3 を
を
- 良い手でもスペードが 5 枚しかなければパスするというのは,もったいないような気がしますが …。
―― ここでは,パスすることにより,「5 枚」をパートナーに伝えることが大切です。 もしもパートナーのスペードが 4 枚ならば, パートナーが 3
 を
ビッドしてくれるでしょう。
を
ビッドしてくれるでしょう。
North の手がちょっと良いからといって 5 枚のスペードで 3 を
ビッドすると,South はスペードの枚数を誤解するので,
LoTT に基づく判断を正確にできなくなってしまいます。
を
ビッドすると,South はスペードの枚数を誤解するので,
LoTT に基づく判断を正確にできなくなってしまいます。 - 他にも例はありますか ?
―― ひとつ,分かりやすい例を挙げましょう。 Q 7 3
Q 7 3
 9 8
9 8
 Q 10 2
Q 10 2
 A 9 6 4 3
A 9 6 4 3
( 8 HCP ) West North East South 1 
パス 1 
X パス ?
あなたは North にいて,この手を持っています。
右オポが 1 オープン。
オープン。
何もビッドできる手ではないので,パスしました。
すると,左オポが 1 をビッド。
をビッド。
これにパートナーがテイクアウト・ダブルを掛けました。 - それなら,一番長いクラブをジャンプしないで,2
 .
.
―― はい。問題は,その後です。
この 2 をビッドするとき,
次回に 3
をビッドするとき,
次回に 3 まで競り合う覚悟ですか ?
まで競り合う覚悟ですか ?
- あっ,そうですね。
パートナーのテイクアウト・ダブルは, と
と  の 2 スートに
それぞれ 4 枚を保証している。だから,
の 2 スートに
それぞれ 4 枚を保証している。だから, は 合計 9 枚ある。
は 合計 9 枚ある。
「安全な代のルール」に頼って,3 まではビッドできます。
まではビッドできます。
―― はい。
- それで,結局のところ,LoTT はどの程度 役に立つのでしょうか ?
―― それは,むずかしい質問です。
Vernes さんも Cohen さんも,LoTT を1つの "道具" として考えている。
"道具" ということの意味を理解してもらうために,4‐3‐2‐1 ポイント・カウント法と比較しています。
もともと,ポイント・カウント法の無かった時代のブリッジは,ハンドの評価が難しかったはずです。 でも,ポイント・カウント法が導入されて, ハンド評価がしやすくなるにつれて, ブリッジのビッドは進化してきました。
LoTT もこれと同じだと言うのです。
LoTT という道具を使って どうビッドするのがよいかは,これから多くの人が考えていくべき課題であって,「我々は 皆,LoTT のパイオニアだ」と言っています。 - でも,LoTT は 常に成り立つとは限らない。
―― はい。いつでも厳密に成り立つとは限りません。
上の「補正」のところに書いたようなことがあります。
本来,LoTT は (切り札の枚数を変えずに) カードの入れ換えをしても,合計トリック数が不変なことが「売り」なのですが,実際には,変化することがあります。極端な場合には,同じハンドでも,どちらのプレイヤーがディクレアラーになるかによって,取れるトリック数が変わります。 - 常に成り立つとは限らないのだったら,あまり意味が無いのでは?
―― でも,ポイント・カウント法と比べると,よく分かります。
25~26 pts あれば 必ずゲームができる というわけではありません。
たとえば,
26 pts あったからゲームをビッドした … それなのにダウンした。
という場合,
ポイント・カウント法は不正確だ … ポイント・カウント法は止めよう !
ということにはならない。 - そうですね。
―― ここのところは,Cohen さんの受け売りをしているだけなのですが,
LoTT についても同じように考えましょう。
ポイント・カウント法が判断の一つの基準になっているのと同じ意味で,競り合いのビッドでは,LoTT を判断の基準として使いましょう。
これまで競り合いのビッドでは,判断基準が何も無かったのに比べたら, 状況はずっと改善されています。
ただし,その数字を鵜呑みにするのではなくて,成り立たなかったからというので文句を言うのではなくて,自分で判断するときの一つの大切な道具として取り入れましょう。 - うーん。なんだか,分かったような分からないような …。
―― それでは,LoTT をもっと身近に感じられるように,ウィーク 2 へ話を切り替えましょう。
- この「ウィーク 2 」というのは,普通の ウィーク 2 オープンのことですか ?
―― はい,そうです。たとえば, この手を持っているとき,いきなり 2 K Q 9 7 6 2
K Q 9 7 6 2
 9
9
 Q 10 8 4
Q 10 8 4
 7 3
7 3
( 7 HCP )  オープンします。
オープンします。
あるいは,右オポが 1 の代でオープンしたときには,ジャンプ して 2 オーバーコールします。
オーバーコールします。
- それは,よく知っています …。
でも,念のために,ウィーク 2 の条件を,ここで復習していただけませんか ?―― ウィーク 2 (あるいは,2 の代のジャンプオーバーコール) の基本要件は
- (1) 5 〜10 HCP を持っている。
- (2) 6 枚のしっかりしたスートを持っている。
( できることなら,A〜10 のうちの 3 枚を含む )
- (3) ほかに 4 枚のメジャースートが無い。
- (4) ボイドが無い。
- それで …,その ウィーク 2 のビッドが LoTT と関係あるんですか ?
―― はい。あります。
 K Q 9 7 6 2
K Q 9 7 6 2
 9
9
 Q 10 8 4
Q 10 8 4
 7 3
7 3
( 7 HCP )
あなたがスペードを 6 枚持っています。
このとき,残りの 7 枚が残りの三人に平均して 配られていると仮定すると,パートナーに 2 枚のスペードを期待できる。したがって, 味方に合計 8 枚のスペードを期待できます (すぐ下の 表(1) が示すように,この確率は 76.3 % です)。
ところで,味方に 8 枚のフィットがある場合,(後に示す表(2) から分かるように) 100 − 14.81 = 85.2% の確率で,相手方にも 8 枚以上のフィットがある。このとき,切り札の合計枚数は, 8+8=16 以上です。
ここで LoTT を適用するとどうなりますか ? - なんだか,「風が吹けば桶屋が …」というような話の進め方ですが …。
でも 一応そうだとすると, LoTT によれば,合計のトリック数が 16 以上になる。そこから先は,チャートを 作ってみないと分からない …。――「安全な代のルール」を適用すれば,チャートの必要はありませんが, 正確な議論には,合計トリック数が 16 の場合のチャートが必要です。
作ってみましょう。合計トリック数 16 の場合のチャート 双方ともバル N-S play 2 
W-E play 2 
N-S Tricks N-S Score W-E Tricks N-S Score 9 +140 7 +100 8 +110 8 −110 7 −100 9 −140 6 −200 10 −620 (4  )
)
- だったら,ここでは 断然 ウィーク 2
 をビッド!
をビッド!
結局,ここでの話はどういうことを ?―― はじめに書いた ウィーク 2 の条件 (2) は, LoTT を知らない人でも,「そうビッドするものだ」と 教えられて使っています。
でもなぜ 6 枚か, という理由を知らずに使っています。
LoTT を知ると,「6枚」の理由が,上のように理解できます。
- その話は,もっと高い代にも当てはまるのですか ?
―― はい。高い代のプリエンプトにも,当てはまります。
2 つの例を考えてみましょう。
はじめに,まず,この場合 …。 K Q 10 7 6 5 2
K Q 10 7 6 5 2
 8 4
8 4
 10
10
 9 4 3
9 4 3
( 5 HCP ) - これなら,もちろん,3
 をビッドします。スペードが 7 枚
ありますから。
をビッドします。スペードが 7 枚
ありますから。
―― はい。確かにそうですね。それで,さっきと同様に,切り札のフィット確率を調べてみましょう。 確率の表 (1) を見ると,パートナーが持つスペードの枚数は,
1 枚以上が 92.9%,であることが分かります。
2 枚以上が 66.7% (100 − ( 7.1 + 26.2 ) = 66.7).
上の行の確率 92.9% は,当然のことながら,ほとんど 100% です。
下の行の確率は,3 回に 2 回の割合で,合計 9 枚のフィットが発生することを示します。 - それだったら,「安全な代のルール」に従って,ほぼ安全に 3
 を
ビッドできる。
を
ビッドできる。
あぁ,なるほど,この場合にも ( ウィーク 2 のときと同様に ),安全な代のルールとフィット確率から,普通の プリエンプトをしてよいことが分かる。―― はい。さっきと同じように考えるなら,同じように もう一歩踏み込んで調べることができます。
味方が合計 9 枚のスペードを持っているとき,相手方の切り札の枚数は,どれくらいでしょうか ?
その答が,フィット確率の表(2) です。 - その表を見ると …。あちらの切り札は,少なくとも 8 枚ある。
―― しかも 8 枚の単純フィットの確率は全体の 1/4 (23.33%) に過ぎない。 残りは,8 枚のダブルフィットとか,9 枚以上のフィットです。
- それなら,切り札の合計枚数は最低でも 9 + 8 = 17 だから,
正確な議論のために,17 としてチャートを作ってみましょう。
―― はい。結論は既に見えていますが,この作業を実際にやってみると理解が深くなると思います。
合計トリック数 17 の場合のチャート 双方とも バル N-S play 3 
W-E play 3 
N-S Tricks N-S Score W-E Tricks N-S Score 10 620 (4  )
)7 +200 9 +140 8 +100 8 −100 9 −140 7 −200 10 −620 (4  )
)
- 確かに,結論は明瞭です。ここでも,「ルール」がプリエンプトを安全に
守ってくれることが分かります。
―― つまり,話は,さっきの ウィーク 2 と同様です。
上のような手で 3 とプリエンプトすることは,
初級者も 教えられて知っています。でも 7 枚の理由までは 教えてもらわなかったでしょう。
とプリエンプトすることは,
初級者も 教えられて知っています。でも 7 枚の理由までは 教えてもらわなかったでしょう。
「法則」と「ルール」,それに確率の知識を加えると,その理由を正確に理解できます。 - もうひとつの例とは ?
―― これも,よくご存じの例です。オークションが こんなふうに進みました。 パートナーが 1West North East South 1 
パス ?  で オープン,それを右オポがパスして,ビッドの順番があなたに回ってきた。あなたの手は,こんなふうです。
で オープン,それを右オポがパスして,ビッドの順番があなたに回ってきた。あなたの手は,こんなふうです。
 J 10 5
J 10 5
 J 10 7 3 2
J 10 7 3 2
 Q 5 4 3
Q 5 4 3
 4
4
( 4 HCP ) West North East South 1 
パス 4 
- これは 僅か 4 HCP の弱い手 …,でも ハートが 5 枚あって,クラブがシングルトン。
こういう場合には,絵札がぜんぜん無いときでも 4
 をビッドする … と習いました。
をビッドする … と習いました。
―― その理由も習いましたか ?
- 相手側が 4
 を見つける前に,先行してプリエンプトするのだと …。
を見つける前に,先行してプリエンプトするのだと …。
―― では,ここでも LoTT に基づいて判断してみましょう。
- それは,簡単ですね。「安全な代のルール」を使えば,4 の代まで安全に競り合えることが保証される。
こちらには切り札が 10 枚あることが,もう分かっているから。―― 確かにその通りですが,もう一歩踏み込みましょう。
こちらに切り札が 10 枚あるとき,相手の切り札は,最低,何枚でしょうか ?
7 枚でしょうか,それとも 8 枚,いや 9 枚以上 ?
この状況で,相手の切り札を何枚と想定するか ?LoTT に基づいて競り合うときには,常に これを自分に問い掛けます。
さきほど見た フィット確率の表(2) をもう一度 見ると,相手には 少なくとも 8 枚のダブル・フィットがある (22.68%)。 これは,単純な 8 枚フィットではありません。2 スートで 8 枚フィットがある。 ここで,Vernes さんも Cohen さんもダブル・フィットの場合に 正の補正を加えることを 思い出すと …。 - あぁ,分かります。ぼこさんが何を言いたいのか。
こちらには 切り札が 10 枚ある。相手には最低でも 8 枚ある。
だから,合計枚数は,10 + 8 = 18 枚。したがって,LoTT は 合計 18 トリックを 予測する。
ただし 8 枚だと想定しても,それはダブル・フィット。 そこで,プラスの補正をして,19 と考える。そう考えたとしても これは ミニマムに過ぎない。もっと大きいかも知れない。 でも,一応,合計トリック数を 19 として,チャートを作ってみましょう。
―― このチャートは,とても単純ですから,作るまでもなかったでしょうが, ここでも,4合計トリック数 19 の場合のチャート 双方とも バル N-S play 4 
W-E play 3 
N-S Tricks N-S Score W-E Tricks N-S Score 11 +650 8 +100 10 +620 9 −140 9 −200(x) 10 −620 (4  )
)
8 −500(x) 11 −650 (4  )
)
 とプリエンプトする理由がよく理解できたと
思います。
とプリエンプトする理由がよく理解できたと
思います。
最後に 3 番目の例を挙げます。
West North East South 2 
Pass ?
パートナーが 2 で
オープンしました。これに何と応えるかという問題です。
で
オープンしました。これに何と応えるかという問題です。
あなたの手は,こんなふうです。
ここで 何をコールしますか ? 競り合いは,まだ発生していません。 10 9 4 2
10 9 4 2
 J 8 7 3
J 8 7 3
 K 9 3 2
K 9 3 2
 4
4
( 4 HCP ) - そうですね …。これも僅か 4 HCP のとても弱い手。だから,3
 , … いや,
スペードが合計 10 枚あるから 4
, … いや,
スペードが合計 10 枚あるから 4 かな。
かな。
―― その判断は もうお任せします。
私自身について言うと,未だ LoTT について何も知らないとき,ビッドについては Mike Lawrence の本でいろいろ学びました。Lawrence は,上のような状況では, (たとえ絵札が全く無くても,切り札 5 枚とシングルトンがあれば) 直ちに 4 をビッドするよう TIP (秘訣) として教えています。
をビッドするよう TIP (秘訣) として教えています。
- 結局のところ,どういうことが言いたいのですか ? ぼこさん。
―― あっ,ごめんなさい。
LoTT とそれに関連したことを学んでしまうと,それまで専門家が TIP として教えてくれていたことが自明に見えてくる … と言いたかったのです。
- ちょっと LoTT から脱線になるかも知れませんが …,
上の説明では,私が切り札を 6 枚持っているとき,パートナーは平均すると 2 枚 持っているということでしたね。―― はい。
- 正確に確率を計算すると,どうなるのでしょうか?
―― この計算は 割合に容易なので,正確に計算してみました。その結果は,次のようになります。
計算の方法は別のページに 説明してありますので,計算式に関心のある方は,そちらをお読み下さい。《 確率の表 (1) 》 同一スートでの 自分の枚数とパートナーの枚数の相関 [ 数値は 発生確率(%) ] 自分の
枚数8 枚
以上のフィット
確率パートナーの枚数 0 1 2 3 4 5 6 7 8 9 10 11 12 13 0 1.2 0.1 1.5 7.4 18.7 27.5 24.8 13.9 4.9 1.0 0.1 0.0 0.0 0.0 0.0 1 3.4 0.2 2.6 10.6 22.9 28.6 21.6 10.1 2.9 0.5 0.0 0.0 0.0 0.0 2 8.5 0.5 4.1 14.5 26.7 28.1 17.7 6.7 1.5 0.2 0.0 0.0 0.0 3 18.1 0.8 6.4 19.2 29.6 25.9 13.3 4.0 0.7 0.1 0.0 0.0 4 33.7 1.5 9.6 24.2 31.1 22.2 9.1 2.1 0.3 0.0 0.0 5 54.4 2.5 13.9 29.2 30.6 17.4 5.4 0.9 0.1 0.0 6 76.3 4.3 19.5 33.4 27.8 12.1 2.7 0.3 0.0 7 92.9 7.1 26.2 35.7 22.8 7.1 1.0 0.1 8 100 11.4 33.8 35.2 16.1 3.2 0.2 9 100 18.2 41.1 30.8 9.0 0.9 10 100 28.4 46.2 22.2 3.1 11 100 43.9 45.6 10.5 12 100 66.7 33.3 13 100 100 - この表の見方は?
―― あなたが,
 を 6 枚持っているとします。
このとき,パートナーが
を 6 枚持っているとします。
このとき,パートナーが  を持つ確率は
を持つ確率は
2 枚の場合が 33.4 %
3 枚の場合が 27.8 %
4 枚の場合が 12.1 %
…
それで,合計 8 枚ならフィットがあると考えてこれらを合計すると, でフィットのある確率が 76.3 % と
なります。
でフィットのある確率が 76.3 % と
なります。 - この確率 76.3 % がかなり高いので,6 枚の良い
スートがあったら,パートナーに 2 枚以上を
期待してプリエンプトしてよい … ということなのですね。
―― はい,そうです。
自分で 6 枚持っていれば,4 回のうち 3 回はフィットがあります。
- うーん。
―― まだ何か ?
- Weak 2 や 3 以上の代のプリエンプトは,さっきのようなう説明だと,確かに自分の感じとつながってくるから,LoTT が身近に感じられるってことは,
それはその通りなんだけど。でも …。
―― でも ? LoTT というのがよく分からない ?
- いいえ。それはいいんです。とりあえず,LoTT がよく成り立つということらしいから …。でも,
なんだか話がずれてきているように思うんです。
―― どういうふうにずれて ?
- だって,はじめのところでは,LoTT は競り合いの状況で役に立つということでしたね。両方の側がビッドして
競り合ったときに,どの代までビッドするか … そのとき
味方の切り札の合計枚数に相当する代まで安全にビッドできるという「安全な代のルール」を使う …。
その根拠が LoTT と「チャート」でした。―― はい。その通りです。
- そこまでは一応分かったんだけど,でも,上のプリエンプトの場合だと,話が違う。
―― どう違う ?
- だって,たとえば,味方が切り札を 10 枚持っているから 4 の代でプリエンプトする。でも,このとき,
相手側に切り札が何枚あるかは 未だ分かっていませんね。
―― 確かに,まだ,分かっていません。
- もしも相手側も切り札を 10 枚持っていれば,LoTT に頼ってプリエンプトするのが正解でしょう。
でも,もしかして相手の切り札は 7 枚かも知れない。
そしたら,合計トリック数は
10 + 7 = 17
だから 4 の代でプリエンプトするのは損ですね。かといって,ここでパスすると相手の方が 10 枚フィットを 見つけてしまうかも知れない。プリエンプトというのは,その前にしないと意味がないものだし …。
ぼこさんの説明では,そこのところで確率の表とかいうのを持ち出してきて, …。―― LoTT を忠実に守ろうとすると,相手側の情報が確定していない段階では,ビッドの しようがないということですか … ?
- はい。そぅ,そういうことです。
LoTT は,両方の切り札の枚数が分かっていることが前提ですから。―― LoTT をよく理解なさっている …。
- そんなんじゃ,答になっていませんよ。ここから先はどう考えるのですか,LoTT の精神を活かすには ?
―― 実は,LoTT だけでは,ここで行き止まりなのです。考えようがありません。
- では,もうこれ以上どうしようもないと ?
―― いいえ,そうではありません。
これ以上考えるには,確率について理解していることが必要です。
たとえば,あなたが さっき言ったような場合,
こちらの切り札が 10 枚のとき,相手側の切り札が 7 枚の確率は ?
というような問題です。 - そうですね。それで,その確率はいくらなのですか ?
―― ゼロです。
- ほんとのゼロ ?
―― はい。数学でいうゼロです。
つまり,そういうことは絶対にありません。 - ということは,こちらに切り札が 10 枚あれば,相手側の切り札は必ず 8 枚以上,ということですか ?
―― はい,そうです。
- この表題の「切り札の偏りかた」とは,何枚の切り札がどういう確率で起こるか,ということでしょうか ?
―― はい。切り札の枚数の確率分布について計算した結果をお話ししたいと思います。
まずは,簡単な結果から …。《 確率の表 (4) 》 枚数 7 8 9 10 11 12 13 確率(%) 15.7 45.7 28.1 8.7 1.6 0.16 0.01 - この表の意味は,たぶん,私とパートナーの切り札の合計枚数は 8 枚のことが一番多くて,その確率が 45.7% ということなんですね。
―― はい。そうです。 8 枚というのがほぼ 5 割の確率で起こります。
その次に多いのが 9 枚で 30% 近い。 9 枚の確率は,7 枚の確率のほぼ 2 倍です。 - 10 枚フィットが 8.7% もあるんですね。ほぼ 11 回に 1 回の割合で 10 枚フィットがある。
これは予想外に大きいです。11 枚以上のフィットとなると,さすがにぐーんと減りますね。
―― はい。
- でも,この結果だけではあまり意味がありませんね。私たちに 8 枚フィットがあるときに,相手の側に
どういうフィットが起こりやすいとか …。
そこが問題なのではありませんか ?―― おっしゃる通りです。で,その意味での確率を計算しました。
その結果が下の表です。« 確率の表 (2) » 味方の切り札枚数と相手方の切り札枚数 との相関 (発生確率 %) [8d] = 8 + 8; [9d] = 9 + 8 & 9 + 9. 味方の
枚数相手方の枚数 7 8 8d 9 9d 10 11 12 13 Frequency 7 66.67 33.33 * * * * * * * 15.74% 8 14.81 66.67 * 18.52 * * * * * 35.41% 8d * * 32.11 47.57 * 19.03 1.30 * * 10.34% 9 * 32.43 24.32 36.04 * 7.21 * * * 20.22% 9d * * * * 55.99 33.50 9.66 0.82 0.02 7.88% 10 * * 22.68 16.80 30.45 23.43 5.85 0.75 0.04 8.67% 11 * * 8.48 * 48.16 32.10 9.67 1.49 0.09 1.58% 12 * * * * 41.00 41.17 14.94 2.69 0.19 0.16% 13 * * * * 24.30 48.60 22.08 4.64 0.38 0.01%
- この表の見出しで,8d とか 9d と書いてあるのは,どういう意味ですか ?
―― それは,ダブル・フィットです。 8d は,2 スートでの 8 枚フィットを意味します。 8 枚のダブル・フィット [8d] は, 9 枚フィット [9] と同等以上のパワーがあると考えて,この表では別建てで数えました。
それから,9d の欄には,[ 9枚+8枚] と [ 9枚+9枚] という 2 種類のダブル・フィットを 合算して集計しています。 - 星印 (*) は ?
―― それは,ありえない (不可能な) 場合です。
確率の値が正確に 0 になります。 - そぅですか。よく分かりませんが …。
最初に,味方が 7 枚フィットのところを見ると …,
相手の側には 7 枚か 8 枚のフィットしかない。
9 枚以上のフィットは 無いのですね。どうして そういうことになるのかな ?―― 具体的に考えてみましょう。
味方が最高で 7 枚のフィットしか無いのは,2 つの場合だけです。
あなたとパートナーのカードを一緒にして,4 スートでの枚数分布を調べると
(A) 7‐7‐6‐6
(B) 7‐7‐7‐5
この 2 通りしかありえません。 - うーんと。あっ,そうか。 8 枚は持っていないんだから。
それに全部で 26 枚なんだから,確かに この 2 通りしかありえない …。―― それで,このとき,相手の側が持っているカードの枚数分布は,どうなりますか ?
- それは,簡単です。上の裏返しになるから,13 の補数を取って
(A') 6‐6‐7‐7
(B') 6‐6‐6‐8
となる。だから,(A) の場合は,相手は 7 枚フィットで,(B) の場合は 8 枚フィットですね。―― はい。その通りです。
- だから,相手には 9 枚以上のフィットは ありえないというわけか …
なるほど。
それで,その 2 つの場合の確率の比が 2:1 になっているようですが,
正確に 2 : 1 なのですか ?―― はい。別のページで確率の計算方法を説明しています。
- では,次に,表 (2) で,こちらが 8 枚フィットの場合に進むと …,
相手には 11 枚フィットまで ありうる。ずいぶん違いますね。―― はい。こちらに 8 枚フィットがあれば,相手側には ほとんど確実に ( ほぼ 90% の確率で) 8 枚以上のフィットがあります。
面白いことに,全体として,こちらがよくフィットしていれば,相手もよくフィットしています。 つまり,カードの強さの分布はハンドによってまちまちですが,カードの枚数の分布は,かなり公平です。
競り合いのビッドを考えるときに,これは重要です。
LoTT に基づく判断が実際のオークションで有効なのは,このためです。 - でも,こちらの 8 枚フィットに対して,相手側には 10 枚フィット(4.3%) とか 11 枚フィット(0.3%) が
僅かな確率で起こりうる …。
その場合は,あまり,公平とは言えないように思いますが (^。^) …。
―― それは,こちらが単純な 8 枚フィット [8] ではなくて,2 スートで 8 枚フィットがあるダブル・フィットの場合 [8d] です。
[8] と [8d] では,状況にかなりの違いがあることが,この表から分かります。 - そうですね …。
こちらに 10 枚フィットがある場合は …。
―― それは,プリエンプトでオープンするような場合と関係してきます。
ひとつ非常に はっきりしているのは味方に 10 枚フィットがあれば,相手方にはということです。単純な 8 枚フィットではなくて,ダブル・フィットです。
最低でも 8 枚のダブル・フィットがある
10 枚フィットの場合には, この点をよく知っている必要があります。 - そのこと (相手方に 8 枚のダブル・フィットがあること) は,簡単に説明できますか ?
―― はい。簡単です。さっきの 7 枚フィットのときと同じように考えます。 こちらがどれかのスートに 10 枚を持っていると,相手側は,そのスートに
13 − 10 = 3 枚
持っています。さっきと同じように相手方の枚数分布を考えると,最高 8 枚のフィットの場合
3‐8‐8‐7
という分布しかありえません。これが,8 枚のダブル・フィットです。おまけに …。 - おまけに ?
―― おまけに,8 枚ダブル・フィットの発生確率は 22.7% です。 逆に言うと,77.3% の確率で,相手方の切り札は 9 枚以上あります(さっきの表を参照)。
- ということは,味方が切り札 10 枚の弱い手の場合には,合計トリック数は (確率から考えても) 多いと考えられるので,
相手方の切り札枚数が不明であっても,先んじて プリエンプトして損は無い,ということでしょうか。
―― はい。そう思います。
[付記] 実は,上のような表は,Cohen さんの 2 冊目の本の末尾 (p.148) に付録の ような形で載っていて, 1000 ディールでのコンピュータ・シミュレーションの結果が書かれています。
これが,最初の疑問への答えです。
また,Cheung さんのサイトには,もっと精度の高い数値が載っています。
でも,どちらも単純な 8 枚フィットと 8 枚のダブル・フィットを区別して いません。こちらに 10 枚フィットがある場合,相手側の 8 枚フィットは,すべてダブル・フィットなのです。
- この表題に書いてある「ましな」とは,どういう意味ですか ?
ぼこさん,まさか LoTT の改良版を提案なさろうとか …―― そんなに大それたことでは ありません。
細かい話なので,LoTT そのものを 勉強したい人は,この節を読み飛ばして下さい。 - でも,気になりますね。どういうことですか ?
―― これまで何度も出てきたように,
[A] 合計トリック数 = 切り札の合計枚数これが, LoTT 公式です。
これが どの程度よく成り立つかは,これまで説明してきました。
人により意見はさまざまですが,でも,上の公式がすべての土台です。
ところが,その後 Ginsberg さんの研究を読み,また,自分なりに LoTTanalyzer というソフトウェアを開発して,少し考えました。
その結論を書くと,上の公式よりも[B] 合計トリック数 = 最長スートの合計枚数この方が,ちょっぴりですが,正確だと気がついたのです。 - 普通は一番長いスートが切り札になるから,どちらでも同じではありませんか ?
―― 確かに,多くの場合,その通りです。でも たとえば,8 枚のNorth  A J 7 5 4 2
A J 7 5 4 2
 J 2
J 2
 K J 6 3
K J 6 3
West  J
J
East  10 6
10 6
 K 8
K 8
 Q 10 9 7
Q 10 9 7
 A K 5 4
A K 5 4
 10 9 8
10 9 8
 A 4
A 4
 A Q 7 5
A Q 7 5
 10 8 4 3 2
10 8 4 3 2
 Q 9 3
Q 9 3
 8 6 3
8 6 3
 Q 7 5 2
Q 7 5 2
 K 9 6
K 9 6
South  が切り札のときに
が切り札のときに  が 9 枚ということもありえます。
が 9 枚ということもありえます。
他のところにも出てきたハンドですが,例を挙げましょう。 - 取れるトリック数は …
N-S は, を切り札にして 8 トリック。
E-W は,
を切り札にして 8 トリック。
E-W は, または
または  を切り札にして 10 トリック。したがって,合計トリック数は,8 + 10 = 18 です。
を切り札にして 10 トリック。したがって,合計トリック数は,8 + 10 = 18 です。
―― そうですね。次に,切り札の枚数を数えると,N-S のスペードは 9 枚です。 E-W の自然なコントラクトは 4
 なので,
なので, の枚数 8 をこれに加えると,
の枚数 8 をこれに加えると,
[A] 切り札の合計枚数 = 9 + 8 = 17
となります。
一方,不自然なコントラクト 4 を仮定すると,クラブが 9 枚なので,
を仮定すると,クラブが 9 枚なので,
[B] 最長スートの合計枚数 = 9 + 9 = 18
となります。 この場合,公式 [A] と [B] では,右辺の数値が異なり,[B] の方が正確です。 つまり,サイド・スートに長いのがあれば,そちらの長さを採用すべきです。
実際,このハンドの場合, が長いお蔭で,4
が長いお蔭で,4 が成立します。
が成立します。
- でも,それは,前に出てきたダブル・フィットに場合に当たるから,
補正とか調整をすればいいですね。
―― おっしゃる通りです。
だから,この話は「細かい」と冒頭に断ったのです。
でも,「補正」とか「調整」という言葉が出てくるのは, 公式として [A] を土台にしているからです。 [B] を出発点にすれば,このディールについて 補正も調整も必要ありません。 だから,長いスートの枚数が確定していれば,[B] を使う方が妥当だと思うのです。 - そういうことなら,統計的に見て [A] と [B] のどちらの
公式が正しいのですか ?
―― ずっと前の節で Ginsberg さんのお仕事 (1996年) に触れました。
ランダムに発生させた 446,741 個のディールについて,コンピュータによりダブル・ダミー解析 した結果として得られたものです。
その研究で,"LoTT" として採用しているのは,実は [A] ではなく,[B] だったのです。 つまり,ハンドの中身を調べるのは面倒なので,一番長いスートを機械的に切り札と仮定して, LoTT 公式 [B] が非常によく成り立つことを確認なさいました。 - そうだったんですか …。
では,もしも 杓子定規に [A] を採用すると, どうなるのですか ?―― 上の議論から推測できるはずです。平均的に見て,[A] の方が大きな補正を必要とします。 したがって,[A] よりも [B] の方が,統計的に見て,精度が高いことは明らかです。
念のために,私のソフトウェア LoTTanalyzer を使って,これを検証しました。 詳しくは,続編をご覧いただくとして,ここでは,グラフによる比較を示しましょう。
2 つのグラフが並んでいますが,どちらも Ginsberg さんのダブルダミー・ライブラリを使って, LoTTanalyzer から 出力させたものです。
横軸は 切り札の合計枚数,縦軸は 合計トリック数 (赤い×印) です。
薄い青色の棒グラフは,頻度を表します。切り札の合計枚数が 20 を越える頻度は低いので,20 あたりからは,結果が信頼できません。したがって,誤差を表す縦の棒線 (エラー・バー) が 次第に長くなります。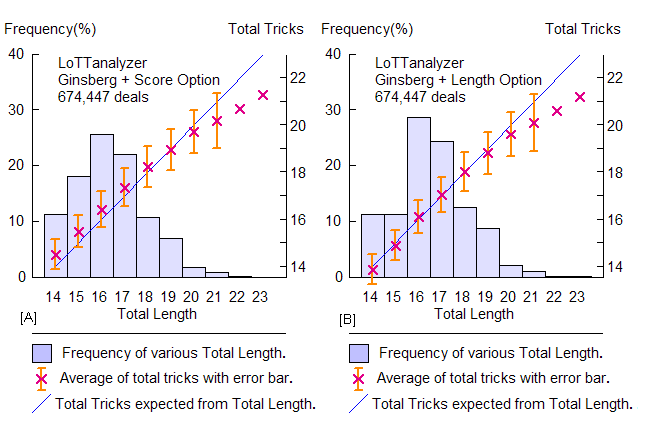
右側 [B] では,Ginsberg さんの流儀に従って,単純に,最も長いスートを切り札として選びます。
この場合,上のハンドでは, E-W のコントラクトが ( 不自然ですが,パート・スコアの ) 4 と
判定されます。そして,合計トリック数が,切り札の合計枚数に一致します。
と
判定されます。そして,合計トリック数が,切り札の合計枚数に一致します。
一方,左側 [A] では,なるべく自然なビッド経過に合うように, スコアを基準にして,コントラクトを判定します。
上のハンドでは,E-W のコントラクトが 4 と判定されます。
そして,合計トリック数は,切り札の合計枚数より 1 だけ大きくなります。
と判定されます。
そして,合計トリック数は,切り札の合計枚数より 1 だけ大きくなります。
これは,もちろん,長いサイド・スート ( ) がトリックを稼ぐからです。
) がトリックを稼ぐからです。
- 2 つのグラフを比べると,右側 [B] の方がよく直線に載っていますね。
―― はい。 この 傾き 45° の直線が LoTT 公式を表します。
ご覧のように,左 [A] は,トリック数を やや ( 0.4 トリック程度) 過少に見積もる傾向があり,その結果, 平均として プラスの補正が必要になります。この傾向は,Vernes さんの分析結果と良く一致します (プラスにずれる 方が,マイナスにずれるよりも多い)。
これに対して,右 [B] は トリック数を (統計的に見て) 正確に見積もるので, 平均的には,補正は不要です。つまり,ビッド経過からサイド・スートの長さについて何らかの情報が掴めるならば, [B] を出発点とするのが最善だ ―― というのが,ここでの結論です。
あるいは,Cohen さんの立場に立つ人に向けては,こういうことが言えるでしょう。 Cohen さんは,公式 [A] は あくまでも出発点であって, 場合に応じて それに 正または負の調整を加える必要がある――とお考えです。
そこでは,原点をゼロとしています。
しかし,LoTTanalyzer から分かったことは,公式 [B] の 原点は確かに 0 であるけれども,公式 [A] では, 原点が 0 ではなく,+0.4 トリックだということです。
したがって,何かの調整を考える際, 平均的には (負の調整よりも) 正の調整の方を 高い頻度で考えるのが妥当です。
単純に言うと,「迷ったときには,プラスの補正を!」ということになるでしょうか。 - [追記] 上のグラフで,切り札 (または 最長スート) の合計枚数が 20 を超えるあたりから,法則のずれは大きくなります。これは,"8枚以上のカードが独立にトリックを稼ぐ" という LoTT のメカニズムから理解できます。枚数が多くなると独立にラフすることはできず,切り札の "相討ち" が発生するからです。
- ノートランプの場合にも,「ちょっぴり増し」なのが 見つかったのですか ?
―― はい。その前に,ノートランプ (NT) の場合の LoTT 公式を復習しておきましょう。 片方が NT をビッドして,他方が 何かのスートをビッドした場合です。
現在 よく知られているのは,Cohen さんの本に載っている[C] 合計トリック数 = スート側の切り札枚数 + 7です。 けれども,NT についても,Vernes さんが自分の公式[D] 合計トリック数 = スート側の切り札枚数 + 8, 7, 6を 最初に考案しました。ここで,右辺に 3 個の数字が書かれているのは,スート側が サイド・スートに ボイド,シングルトン,ダブルトンを持つ場合に対応します。 - この違いも Cohen さんは「調整」で対応するつもりなのでしょうね。
―― はい。そうです。
- それで,ぼこさんのソフトウェアを使うと,何が分かるのですか ?
たとえば,このどちらの方が優れているか …―― 結論を言うと,どちらも だめなのです。
- 駄目って …。どのくらい駄目なのかな。
―― どちらも平均して 1 トリック程度過少評価します。したがって,[C], [D] を額面通りに使うことはできません。
- だったら,額面通りに安心して使える別の公式があるといいですね。
―― はい。それを私が見つけました。と言っても,大きな違いは無いのですが,Vernes さんの公式の右辺に 1 だけ加えます。
[E] 合計トリック数 = スート側の切り札の枚数 + 9, 8, 7自分自身 びっくりしたのですが,これが実によく解析結果と一致します。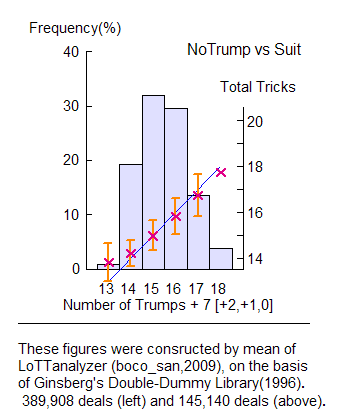
- 公式 [C], [D] の場合の解析結果はどうなのですか。
―― それは かなり悪いので,ここには示しません。
興味がおありでしたら,LoTTanalyzer をダウンロードして,自分でお確かめ下さい。 -
さっきのスートの場合には,わずかな正の補正 (0.4) を考えるということでしたが,ここでは,ずいぶんまた強烈な補正を …。
―― はい。
「ノートランプに対しては,積極的にオーバーコールするのが有効だ」
ということの 《統計的》 裏づけが,ここで得られました。
念のために この結果を正確に表現しておきましょう。
スート側が,サイド・スートに ボイド,シングルトンを持つ場合,公式 [C] による以上に大きな合計トリック数を期待できる。したがって,どちらの側も 安全な代を高く見積もることができる。 - でも,それって Cohen さんが言う調整と同じことでは ?
―― Cohen さんも,きっとあなたに同意なさるでしょう。
でも,その「調整」の中身を考えておきましょう。 - それは,簡単な話でしょう。ボイドやシングルトンがあれば,スート側は
ラフにより トリックを稼げる …。
―― はい。その通りです。
ただし,その場合,その裏返しとして,NT 側は長いスートを持ち, 走る可能性が高くなる。つまり,スート側に ボイドやシングルトンがあれば,NT 側にも ビッドの余地が大きい。 公式 [E] は,この 2 つの事情をうまく取り込んでいると考えられます。[補足説明] NT 側が 長いマイナー・スートで走ることは よくあります。
しかし,私の解析では,NT 側の持ち札の長さを一切調べていません。
したがって,上のグラフでは,横軸に NT 側の長さを考慮していません。