15 ‐17 HCP と 16 ‐18 HCP での 1NT オープンの頻度比較
© boco_san ( ぼこさん 2010 - 2012 ) メイリオ印刷
| いきさつ |
| 結論 |
| 得られた結果の説明 |
| 付録: 確率の計算方法 |
| 付録: 移行の時期 |
| 付録: 確率の計算方法 (2) |
|
付録: 確率の計算方法 (3)
ゲームのある手は 6 回に 1 回 |
いきさつ
1NT オープンは，かつては，16 -18 HCP が標準でした。 しかし，いつの頃からか，これが 15 -17 HCP に変更されて，現在に到っています。 手許の本を比べてみると，この移行の時期は，1980 年代だったことが分かります。
これについて，2009 年 9 月に 「かずちゃんのホームページ」の掲示板で お尋ねしたところ (#690)， 三人の方から 興味深いお答えをいただきました。
同じ頃，Yahoo! のブリッジ･テーブルで，同じ質問を bridge_ski さんにしたところ， 1NT オープンの機会が 30% くらい増える という話でした。
この「30% 増える」という話は，私の耳にずっと残り，いつの日か 自分の手で確かめたいと思っていました。 けれども，この確率の計算は，非常に難しそうで (そもそも どうやって手をつけたらよいのか 皆目分からない) ， 実際，WEB で検索しても，そんな確率は見当たりません。この件は，しばらく忘れていました。
一方，LoTT (合計トリック数の法則) について考えると，切り札のフィットする確率が重要であることに 気づき，その確率の計算に取り組みました。こちらの方は, 考えやすいので，なんとかケリがつき， そこで あらためて (確率計算に慣れたので) 表記の 1NT オープンに取り組みました。
結 論
お急ぎの向きのために，結論から始めます。2 種類のハンド
(A) 15 -17 HCP のバランス･ハンド
(B) 16 -18 HCP のバランス･ハンド
を比較すると，前者が後者の 1.371 倍 多く現れます。つまり，ぶりさんから教えて もらった 30% より少しだけ大きくて，37.1% であることが分かりました。
ここで バランス･ハンドと呼んでいるのは，通常の定義，すなわち，3 種類
[4333], [4432], [5332]
のカード分布を意味します。
ここから先は，上の結果について立ち入って説明します。
詳しい (数学的な) 説明は，付録に回します。
なお，上のように (正しく) バランス･ハンドに限定せずに，シングルトンやボイドを持つハンドも含めて，HCP の大きさだけで
(a) 15 -17 HCP のすべてのハンド
(b) 16 -18 HCP のすべてのハンド
を単純に比較することもできます。これは無意味な比較ですが，(a) は (b) の 1.387 倍 多く現れます。 この数値は WEB 上で 38% として 既に知られています｡
結局のところ，バランス･ハンドに限定しても/しなくても，結論にあまり変わりが無い ことが分かりました。
得られた結果の説明
これは要するに，表題に書いたように，15 ‐17 HCP のバランス･ハンドで 1NT オープンすると，16 ‐18 HCP の場合に比べて，頻度がどのくらい増加するか という問題です。
ひとりのプレイヤーに 13 枚のカードを配る組み合わせは，
52C13 = 635,013,559,600 通り
あります。
これを単純に HCP に従って 0 〜37 HCP (上限は，40 HCP ではありません) に分類することもできますが， それだけでは，上の問題の答になりません｡
1NT オープンでは，手の形を上の 3 種類のバランス･ハンドに限定する必要があります。 これらのバランス･ハンドは，上記の 6350 億通りのうちの 47.6 % を占めます (13 枚のカードの形は全部で 39 通りあるので，バランス･ハンド 3 種類だけで 全体の半分を占める ―― というのは，ちょっと意外です)。
ほぼ 2 回に 1 回の割合でバランス･ハンドが来るので，バランス･ハンドでのオープニング･ビッドは重要です。
そういう訳で，ここでは，6350 億通りのハンドを，その «形» と «HCP» の両方により 分類して，その個数をカウントしました。 そして，得られた結果を，2 つの巨大な表
(1) ハンドの個数
(2) ハンドの発生確率 (単位は ‰ = 1/1000)
として まとめました。それぞれ，クリックしてご覧下さい。
どちらの表も，38 行 × 39 列 = 1,482 個の欄から成ります。
表 (1) は，手の形と HCP ごとに，場合の数を数えた結果です。これらの総計は， 表の右下にあるように，6350億 です。
これらの個数を それぞれ 単純に 6350 億で割ることにより 発生確率が得られ，その結果が 表 (2) に示されています。
この表 (2) で，0 と書かれている欄は，確率の数値が 0.001 % 未満であって 0 ではない ことを意味します。いっぽう，空欄は，確率が厳密に 0 であること (すなわち，そういう場合は絶対に無い) ことを意味します。
分割が非常に細かいために それぞれの確率の数値が小さくなるので，単位を % ではなく， ‰ にしました。したがって，その総計は 表の右下にあるように 1000 となります。
| HCP | [4333] | [4432] | [5332] | 合計 | % |
| 15 | 0.469 | 0.958 | 0.688 | 2.115 | (A) 15 ‐17 合計 4.866 |
| 16 | 0.355 | 0.723 | 0.518 | 1.596 | |
| 17 | 0.259 | 0.523 | 0.373 | 1.155 | (B) 16 ‐18 合計 3.550 |
| 18 | 0.180 | 0.363 | 0.256 | 0.799 |
ただし，こちらの表では，確率の単位を ‰ ではなく % にしました。
この抜き出された表から，
(A) 15〜17 と (B) 16〜18 の 発生頻度の比 4.866 / 3.550 = 1.371 が得られます。
結論として， (A) により 1NT オープンすると，(B) による場合よりも 37 % だけ その機会が増えます。平たく言うと，(A) 15 〜17 HCP で 4 回 1NT オープンする間に， (B) 16 〜18 HCP では 3 回しか 1NT オープンできません。
この違いの原因は，15 HCP と 18 HCP で発生確率が非常に異なるためです｡
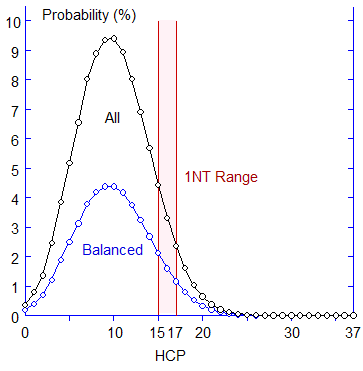この状況は，グラフで見ると よく分かります。
右のグラフは，全ハンド (黒)，バランス･ハンド (青) の発生確率を HCP により分類した結果です｡
さきほど述べたように，黒線は，青線のほぼ 2 倍です。 また，40 HCP を 4 人で分けるので，どちらの曲線も，10 HCP あたりに 山を持ちます。
15 〜18 HCP の範囲は この山の右裾にあるので，
18 HCP を捨てて 15 HCP の
場合を取り込むと， 確率が
かなり増えることが理解でき
ます。
| HCP | % | |
| 15 | 4.425 | (a) 15 ‐17 HCP 合計 10.097 % |
| 16 | 3.311 | |
| 17 | 2.362 | (b) 16 ‐18 HCP 合計 7.278 % |
| 18 | 1.605 |
結局， バランス･ハンドに限定しても しなくても，確率の比は ほとんど同じです。
付録: 確率の計算方法
ひとりのプレイヤーに (52 枚のカードの中から) 13 枚を配る方法は，
52C13 = 635,013,559,600 通りあります。
これらを
1. 手の形により分類する.
2. HCP により分類する.
このように 2 重に分類して ハンド個数を数え上げ，上の表 (1) を作成します。
表 (1) が得られれば，すべての数字を 52C13 で割ることにより，確率の表 (2) が得られます。
はじめに 手の形について考えると，[4333]，[4432]，…，[13,000] の 39 通りあります。
ここで，たとえば，[3424] のような分布を独立に考える必要はありません。[4432] の場合に
多重度 6 を掛ければ十分です。すなわち，この多重度は 4 スートの内容を入れ換えることに対応します。
次に，HCP により更に分類しますが，これが やっかいな作業です。
単純に HCP だけで場合分けするのは，難しくありません。
また，手の形だけで場合分けするのも，難しくありません。
これらの場合の確率の計算方法とその結果は，Durango Bill さんのホームページに載っています。
厄介なのは，ハンドの形を特定して，しかも HCP により分類する ―― という 2 重の拘束条件があるためです。 何かうまい方法があるか (上の 2 通りの場合分けを発展させれば) と思って長い間 考えました。結局は，以下の方法を見つけたのですが，もっと旨い方法があるのかも知れません。
ここには，私なりの考え方を示します。
例として，21.6% という最も頻度の高い形 [4432] で 15 HCP のハンドが何個あるか を数えましょう。
この場合，4 スートの枚数分布は
4 枚，
4 枚，
3 枚，
2 枚
です。
次に，HCP の合計が 15 でなければなりません。
ところで，絵札の持ち方というのは，右の 16 通りの どれかに限られます。
この表には， 4 枚から 0 枚までの絵札の内容と，
それに対応する HCP が 16 通りに分類されています。
そこで，4 スート
に 右の表を上から順番に 割り当てていきます。
最初の候補は，
AKQJ AJxx xxx xx
です。ここでは，スペードに AKQJ (10 HCP), ハートに AJ (5 HCP) を与え， 残りの 7 枚には 屑札 x (10〜2，HCP なし) を与えます。 このとき，6 枚の絵札は完全に指定されましたが， 7 枚の屑札 x には任意性が残っています。
どのスートにも屑札は 9 枚あり，その中から
を選びます。そこで，この選び方に対応して，ハンド個数は，
通りあります。上の表を にらみながら これを続けると，
これらのハンド個数を，許される全ての「絵札の持ち方」について加え，その結果に 多重度 6 を
掛けると 2,976,568,236 という数字 (ほぼ 30 億) が得られます。これが，6350 億個のうち，15 HCP を持つ
[4333] ハンドの個数です。
その発生確率は，30 億 / 6350 億 = 0.469 % と求められます。これが， 前に示した表の左上隅の数値です。
この計算を 39 通りの枚数分布 と 38 通りの HCP という全ての組み合わせ 1,482 通りについて実行した結果が 表 (1) です。
この計算法の要点は，
このアルゴリズムが正しいことは，各行，各列の合計数値が，これとは独立に得られた数値と一致することにより 確かめられます。総数が 52C13 に一致することは， 言うまでもありません。
なお，転記のミスを防ぐため，上の 2 つの表 (1) と (2) の HTML ファイルは，VB プログラムにより直接に作成しました。
この移行がいつ頃だったのかを知ろうと，手許の本･ソフトウェアを調べました。
52C13 = 635,013,559,600 通りあります。
これらを
1. 手の形により分類する.
2. HCP により分類する.
このように 2 重に分類して ハンド個数を数え上げ，上の表 (1) を作成します。
表 (1) が得られれば，すべての数字を 52C13 で割ることにより，確率の表 (2) が得られます。
| 手の形の内容 | 例 | 多重度 |
| すべて異なる | [5431] | 4! = 24 |
| 2 つ 同じ | [4432] | 4! / 2! 2! = 6 |
| 3 つ 同じ | [4333] | 4 |
次に，HCP により更に分類しますが，これが やっかいな作業です。
単純に HCP だけで場合分けするのは，難しくありません。
また，手の形だけで場合分けするのも，難しくありません。
これらの場合の確率の計算方法とその結果は，Durango Bill さんのホームページに載っています。
厄介なのは，ハンドの形を特定して，しかも HCP により分類する ―― という 2 重の拘束条件があるためです。 何かうまい方法があるか (上の 2 通りの場合分けを発展させれば) と思って長い間 考えました。結局は，以下の方法を見つけたのですが，もっと旨い方法があるのかも知れません。
ここには，私なりの考え方を示します。
例として，21.6% という最も頻度の高い形 [4432] で 15 HCP のハンドが何個あるか を数えましょう。
この場合，4 スートの枚数分布は
4 枚， 4 枚， 3 枚， 2 枚
です。
次に，HCP の合計が 15 でなければなりません。
| 絵札枚数 | 絵札 | HCP |
| 4 | AKQJ | 10 |
| 3 | AKQ | 9 |
| 3 | AKJ | 8 |
| 3 | AQJ | 7 |
| 3 | KQJ | 6 |
| 2 | AK | 7 |
| 2 | AQ | 6 |
| 2 | AJ | 5 |
| 2 | KQ | 5 |
| 2 | KJ | 4 |
| 2 | QJ | 3 |
| 1 | A | 4 |
| 1 | K | 3 |
| 1 | Q | 2 |
| 1 | J | 1 |
| 0 | なし | 0 |
そこで，4 スート
に 右の表を上から順番に 割り当てていきます。
最初の候補は，
AKQJ AJxx xxx xx
です。ここでは，スペードに AKQJ (10 HCP), ハートに AJ (5 HCP) を与え， 残りの 7 枚には 屑札 x (10〜2，HCP なし) を与えます。 このとき，6 枚の絵札は完全に指定されましたが， 7 枚の屑札 x には任意性が残っています。
どのスートにも屑札は 9 枚あり，その中から
| スペード: | 9 枚の中から 0 枚， |
| ハート: | 9 枚の中から 2 枚， |
| ダイヤモンド: | 9 枚の中から 3 枚， |
| クラブ: | 9 枚の中から 2 枚 |
| 9C0 × 9C2 × 9C3 × 9C2 = 1 × 36 × 84 × 36 = 108,864 |
| AKQJ
| KQxx
| xxx
| xx
| 9C0 × 9C2 × 9C3 × 9C2 | = 1 × 36 × 84 × 36 |
| AKQJ
| KJxx
| Jxx
| xx
| 9C0 × 9C2 × 9C2 × 9C2 | = 1 × 36 × 36 × 36 |
| AKQJ
| QJxx
| Qxx
| xx
| 9C0 × 9C2 × 9C2 × 9C2 | = 1 × 36 × 36 × 36 |
| AKQJ
| QJxx
| Jxx
| Jx
| 9C0 × 9C2 × 9C2 × 9C1 | = 1 × 36 × 36 × 9 |
| AKQJ
| Axxx
| Jxx
| xx
| 9C0 × 9C3 × 9C2 × 9C2 | = 1 × 84 × 36 × 36 |
| etc. …. |
その発生確率は，30 億 / 6350 億 = 0.469 % と求められます。これが， 前に示した表の左上隅の数値です。
この計算を 39 通りの枚数分布 と 38 通りの HCP という全ての組み合わせ 1,482 通りについて実行した結果が 表 (1) です。
この計算法の要点は，
枚数分布が [4432] で 合計 15 HCP
という条件下で，各スートに右上表のあらゆる組み合わせを許し，そのとき，
カード x が取りうる場合の数 9C屑札枚数 を掛け合わせる
ところにあります。
このアルゴリズムが正しいことは，各行，各列の合計数値が，これとは独立に得られた数値と一致することにより 確かめられます。総数が 52C13 に一致することは， 言うまでもありません。
なお，転記のミスを防ぐため，上の 2 つの表 (1) と (2) の HTML ファイルは，VB プログラムにより直接に作成しました。
移行の時期
この移行がいつ頃だったのかを知ろうと，手許の本･ソフトウェアを調べました。
- (A) Ned Dowley & Ellen Pomer: Standard Bidding with SAYC (2005).
- (A) Fred Gitelman: Learn to Play Bridge (2003).
- (A) Audrey Grant: ACBL Spade Series (2000).
- (A) Barbara Seagram & Marc Smith: 25 Bridge Conventions You Should Know, (1999).
- (A) William S. Root: The ABCs of Bridge (1998).
- (A) Mike Lawrence: Conventions (1996).
- (B) Audrey Grant: ACBL Club Series (1987).
- (B) Charles H. Goren: Goren's New Bridge Complete, (1985)
- (A) William Root & Richard Pavlicek: Modern Bridge Conventions, (1981)
付録: 確率の計算方法 (2)
本稿では，
(1) 手の形により分類する.
(2) HCP により分類する.
という 2 重の条件を課して，場合の数を数えました。条件が 2 重であるために，1,482 通りに 分ける必要が生じ，計算が複雑になりました。
この条件がどちらか片方の場合には，計算がずっと 簡単になります。
この 2 つの場合についても，計算法をここにまとめておきます。
(1) の場合 ( 一人のプレイヤーに配られるハンドの形の分布 ).
| スペード 13 枚 |
| ハート 13 枚 |
| ダイヤモンド 13 枚 |
| クラブ 13 枚 |
手の形 [a, b, c, d] が指定されているので， 52 枚のカードをスート別に 13 枚の 4 つの山に分け，それぞれの山から
a 枚，b 枚，c 枚，d 枚 を抜き出します。
このような場合の数は，
| N [a, b, c, d] = 13Ca × 13Cb × 13Cc × 13Cd |
a + b + c + d = 13
です。ここで， a, b, c, d を入れ換えた場合も 含めて数えるには，これに 多重度 を掛けます。 こうして得られた結果が，さきほどの巨大な表の最下行に示されています。
これをすべての可能な a, b, c, d について加えると， その結果は 52C13 ( = 6350 億) となります(これには，2 項係数の和公式を 3 回使います)。
(2) の場合. ( 一人のプレイヤーに配られる HCP の分布 )
今度は HCP が指定されていて，各スートの枚数は不定なので，少しだけ複雑です。 この場合には，52 枚のカードを，右のように，5 つの山に分けます。
| Ace 4 枚 |
| King 4 枚 |
| Queen 4 枚 |
| Jack 4 枚 |
| 残りの 36 枚 |
そして，それぞれの山から Ace A 枚，King K 枚，Queen Q 枚，Jack J 枚 を抜き取り， 最後の山からは，S 枚の屑札を抜き取ります。 抜き取るカードの枚数が 合計 13 なので，
A + K + Q + J + S = 13
です。また，HCP が指定されているので，このうちのどれか 2 個 ( たとえば，J と S ) は 上式と
4 A + 3 K + 2 Q + J = HCP
により制限されます。したがって，HCP を指定したとき，場合の数は
N (HCP)
=
A, K, Q
4CA × 4CK × 4CQ × 4CJ × 36CS
となります。この右辺は，すべての可能な (階乗記号の中の引数が負にならない範囲で) A, K, Q について加えます。
A, K, Q
4CA × 4CK × 4CQ × 4CJ × 36CS
こうして計算した結果が，さきほどのグラフの黒丸の線です。 なお，これを 0 から 37 HCP まで加えると，その結果は やはり 52C13 (= 6350 億) となります｡
付録: 確率の計算方法 (3)， ペアに配られる HCP の分布
すぐ上で考えたのは，自分ひとりに配られるカードの HCP の分布でした。
同様に考えると，自分とパートナーの二人に配られる HCP の分布も計算できます。 今度も同じように 52 枚のカードを，右のように 5 個の山に分けます。
| Ace 4 枚 |
| King 4 枚 |
| Queen 4 枚 |
| Jack 4 枚 |
| 残りの 36 枚 |
そして，それぞれの山から Ace A 枚，King K 枚，Queen Q 枚，Jack J 枚 を抜き取り， 最後の山からは 屑札 S 枚を抜き取ります。 抜き取るカードの枚数が 合計 26 なので，
A + K + Q + J + S = 26
です。また，HCP が指定されているので，このうちのどれか 2 個 ( たとえば，J と S ) は 上式と
4 A + 3 K + 2 Q + J = HCP
により制限されます。したがって，HCP を指定したとき，場合の数は
N (HCP) = A, K, Q
4CA × 4CK × 4CQ × 4CJ × 36CS
となります。この右辺は，すべての可能な ( 階乗記号の中の引数が負にならない範囲で) A, K, Q について加えます。
さきほどとの違いは，抜き取る枚数が 13 から 26 に変わったことだけです。
これを 0 から 40 HCP まで加えると，その結果は 52C26 となります。
A, K, Q
4CA × 4CK × 4CQ × 4CJ × 36CS
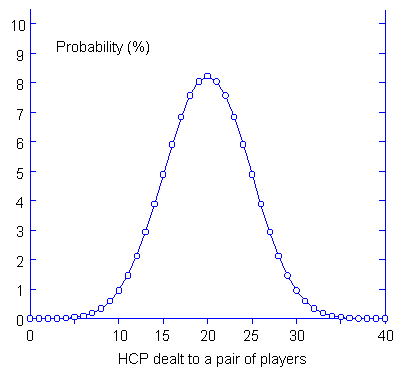この場合の発生確率が 右のグラフです。
横軸は ペアに配られるカード 26 枚の HCP を, 縦軸はその確率 (%) を表します。 当然のことながら，このグラフは HCP = 20 に山を持ち 左右に対称です。 ここで HCP
25 ならば何かのゲームが
あると考えて，25 HCP 以上の確率を合計すると 17.5% という数値が得られます。
すなわち，平均的には，6 回のディールのうちで 1 回程度ゲームがあります。