科学のおかげで、少なくとも先進国の人々の生活は豊かになりました。しかし逆に、科学がこっそりと金主権力者の私的な利益を得る道具として利用されることがないでしょうか？　あるいは、科学的に正しいと称して金主権力者に美味しい事を行っていないでしょうか？

ＣＰＵは本質的に足し算しか出来ないという話をヒントにして、論理演算を二進数１桁で「エセ」数式化してみました。なぜ「エセ」かというと「私が考えた」「一部にのみ注目する」「１桁同士でしか使えない」からです。計算結果のアスタリスク（星印）が付いている桁だけを採ります。ＯＲは初めに足した結果の桁同士を足します。ＮＯＴは１とＸＯＲしたのと結果は同じですから１だけを足します。ＮＯＲやＮＡＮＤはＯＲやＡＮＤの結果に１を足します。ちゃんと結果が合っているでしょ？（注１）ＩＸＯＲでも合いますよ。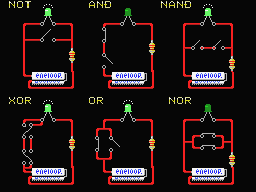

XOR NOT * * 0+0=00 0+1=01 0+1=01 1+1=10 1+0=01 1+1=10 AND NAND * * 0+0=00 +1=01 0+1=01 +1=01 1+0=01 +1=01 1+1=10 +1=10 OR NOR * * 0+0=00 → 0+0=00 +1=01 0+1=01 → 0+1=01 +1=10 1+0=01 → 0+1=01 +1=10 1+1=10 → 1+0=01 +1=10

しかしこれは、あくまで「エセ」です。よく使われる「数字の詐欺」の手口＝都合のいい位置で区切る、都合のいい所だけを採る方法と同じです（注２）。「２値論理（ブール代数）」とか「論理関数」とか「カルノー図」といった、本当の定理や公式とは全く無関係です。ご存知の通り、テレビの情報番組やインフォマーシャルでは、もっとずさんな手口も堂々と行われますが（注３）、上の場合、ちゃんとつじつまは合っているので、その気なら各種の計算にも使え、その結果も正しいのです。

画像をＸＯＲしてフラッシュ

この様に、計算しても合っている「エセ数式」は、数字に弱い・数学の嫌いな文系の私でも作れます。世の中には数字に強い・数学の得意な理工系の悪党は五万と居るでしょう。そういう輩が、ただテレビのＣＭでサギってるだけならまだいいですが、もし金主権力者と結びついた場合は、その害悪たるや計り知れません。ルネッサンス以前の世界に名だたる欧州人学者達が、よってたかって太陽系の惑星の軌道の複雑な計算式を「捏造」し「旧約聖書」に基づく「天動説」を、学問的に正しいものであるかのように仕立て上げていたのと同様に（注４）、一見正しい「エセ」数学による「エセ」数字は、現代でもいたるところに氾濫している様です。数学に限りませんが、日本でも世界でも何故かメディアによって異様に持ち上げられる特定の“学者”や特定の“仮説”があると思いませんか？　物理や数学といえども、その時代の社会制度と密接な関係を持ち、金主や政治権力に左右されているのです。正しいと誰もが信じていた理論や公式が、世界の政治体制の変化で覆るかもしれません。

ページのＴＯＰへもどる

１０の３乗は１０００。１０の２乗は１００。１０の１乗は１０。では、１０の０乗は？

そう、正解は１です。よく説明に使われるのが、図の左の列の「その１」で、「１０倍していくと（あるいは１／１０していくと）そうなるから」というのですが、これだと０乗の０って何？という部分が説明されていなくて、何かすっきりしませんよね。単に順番だから？？
　逆に、左図の右の列「その２」だと、０の意味もバッチリわかりますし、説明に（？）となる所が無いでしょ。代数っぽく１０をＸと置いても、Ｘ＝１Ｘですから、つじつまは合いますし。でも、数学者に言わせると「正しくない説明」なのだそうです。つまり上記「エセ」論理演算と同じく「エセ」数学となるワケです。が、何がいけないのか？　累乗の底や基数が何でも計算も合いますし、むしろ教科書より良いんじゃないの？という「エセ」もあるんですネ。

ページのＴＯＰへもどる

確率は未来を予測できない？　その１

１万枚の封筒に１つだけ当り券が入っているクジがあります。１人につき１枚だけ封筒を引けるとすれば、当たりを引く確率は１万分の１ですよね。さて、９９９８枚が引かれて開封され、全てがハズレでした。開かずに残っているのは２枚です。当り券は当然この２枚の中に入っています。この時、残っている封筒を引いた人の当たる確立はいくらでしょうか？

私は「この時」という言葉があるので、その時点での確率を計算し直さなければダメで、２分の１が正解ではないかと思ったのですが、私の読んだ幾つかの本では、同様の問題に２通りの正解がありました。一つは「開封しようがクジが当たる確率は変わらないので１万分の１」。もう一つは私と同じ様に「２枚のうち１つが当りなのだから２分の１」。どっちが正解（？？）

しかし、同じ出来事の解釈の仕方で確率が変わるなら、確率的な予測って、計算する人の気分しだいなのでしょうか？

確率は未来を予測できない？　その２

２つの箱が有り、一つの箱にはもう一つの２倍の金額が入っています。貴方に１つだけ選んだ箱の中身をくれるそうです。２つに１つですから、２分の１の確率で倍の金額を手にできます。貴方は一つ箱を選びました。開けると１００円が入っていました。この時、もし貴方が開いていない方の箱と交換したければ、交換しても良いそうです。交換した方が得でしょうか？　損でしょうか？　それとも同じでしょうか？

あれっ？　倍の金額を得る確立は２分の１、つまりどっちをとっても同じハズなのに、交換する方が得ですね？　こんなことって・・・。

実はこんな単純そうに見える問題に、明快な解答をした人は居ないそうです。もちろん、数学者は一般人には意味不明な用語で説明するのですが、それは要するに「確率と金額は別だ」（でも金額の確率だよね？）とか、「中を見たら話が違うジャン」（じゃ確率は未来を予測できないんだ？）とか、「ｎ／２より２ｎの方が数直線上に少ない“ハズ”だからそーなる」（エーッ、そうかぁ？）とか、分かった様な分からない様な説明を小難しく言っているだけで、「こーしてこーである」な公式のような綺麗な解答は未だに出せていないのです。

同じ事なのに、中を見るだけで違ってしまうなんて、数学的確率の正確率って、案外ダメダメなのかも？

３つの箱では１つを開けると答えが２つ・・・！？

→

←コレへの私の意見

ページのＴＯＰへもどる

例えば、人類の誰一人ペンギンやイルカを見たことが無いとします。ただし、化石は残っているとします。見たことの無い生き物の生前の姿は、骨格のみからどこまで再現できるでしょうか？　体色や模様、鶏のトサカやクジャクの尾羽みたいなものは、全く判らないでしょうが、体形や動き方なら本当に骨格だけで再現できるでしょうか？
　右の写真の右端が本物のペンギン骨格です。骨だけで組むと、どうしても自然と生体より前かがみに成ります。もし、ペンギンを見たことが無ければ、中央の様に組むでしょう。しかも、これは本物のペンギンもよくとる体勢なので、骨格的にも筋肉の構造的にもおかしくないのです。上がその泳ぐ想像図です。 同じ図の下の左はイルカの一種の骨格です。イルカの類を見たことが無ければ、右の、まるで恐竜時代の海大トカゲ＝モササウルスの様な想像図になるかもしれません。尾びれをつけたとしても、本物の形にはならないでしょう。

左の図は、順にインコ、ニワトリ、ダチョウ、ハト、走るエリマキトガゲの図と、最近のティラノサウルスの想像図（２０１１年現在）です。ティラノサウルスはこういう風に立っているのだそうですが、無理があると思いませんか？
　現在の生物の内、２本足で立って歩く者は全て、じっと立っている場合は肩より頭を上に出します。じっと立っている場合の首は水平面より４５度以上の角度を持つのです。人でも、鳥でも、獣を後ろ足だけで立たせても、エリマキトカゲが走る時でも、です。理由は簡単で“重いモノ（頭）は重心に近く寄せるほどバランスを取り易い”からです。

世界最大の吊り橋 明石海峡大橋

全長3,911ｍ、主塔高さ海上297ｍ（海底からは328ｍ）

仮に尻尾が大きくて重くて、頭とシーソーのようにバランスが取れるとしても、ちょうど長い吊り橋を支える鋼鉄の支柱と鋼鉄のワイヤーの様にとても強力な支えが要ります。しかも、もしそれを保ったまま自在に動くとすれば、ものすごい力が必要なのです。生き物が、常時そんな無駄なエネルギーを使うでしょうか？　そんな非効率な生き物があるでしょうか？　ティラノサウルスが常時この体勢で活動していたとすれば、ひどい肩こりや腰痛に悩まされたことでしょう(^^;)。

安定した恐竜

こちらは、少し前のティラノサウルス想像図です。見るからに安定してますよね。実際、模型を作っても上記の図では、なかなか立たせられませんが、こちらの形にすれば比較的立たせやすいのです。動く時はもっと頭を下げて前傾するにしても、じっと立つ時はこっちに近かったのではないでしょうか？　学者は「コンピューターの計算では今の図になるんだ！！」と言うのでしょうが、コンピューターは計算するだけで、データを入れたり計算式を作り出す、つまり“考え方を考えるのは人間”ですからネ。その内、今の想像図も修正されるような気がしてなりません。どこぞの「パンケーキ理論」と同じように、見て無理があるものは、やっぱり無理が・・・

ページのＴＯＰへもどる

このページは、1024×768画面に合わせて作りました。ちゃんと見えなかったらスミマセン