　　　観測の意味

　【目的】

　シュレーディンガーの猫について一通り理解したあとで、「観測とは何か」という問題を考えよう。それがこのページの目的だ。
　シュレーディンガーの猫については、すでに別の専用ページで、いろいろと詳しく説明した。ただしそこでは、「観測とは何か」については、いささか説明不足のところがあった。
　一方、二重スリットのページでは、こういう趣旨のことを述べた。
　「観測したから、波から粒子になったのではない。波から粒子になったから、観測できるようになったのだ」

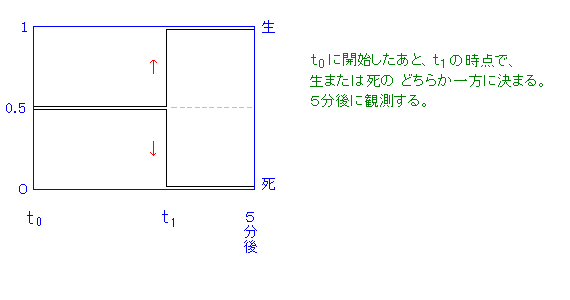
　この新たな説明に基づいて、シュレーディンガーの猫における「観測とは何か」という問題を、説明しよう。わかりやすくするために、図を用いる。

問題の要点

　ここで問題とするのは、「シュレーディンガーの猫のパラドックスはどこにあるか」ということではない。そのことは、別の専用ページで扱った。そして、こう結論した。
　「シュレーディンガーの猫の問題は、量子力学の問題ではなく、論理学の問題だ」

　これはこれでいい。一方、それとは別に、次の問題もある。
　「シュレーディンガーの猫において、観測とは何か？」
　これについては、先の専用ページで、こう述べた。
　「決定と判明とは、別のことである。猫の生死が決定することと、猫の生死が判明することとは、別のことである」
　これで話は一応、片付いている。ただし、よりわかりやすくするために、図によって説明しよう。

ナンドウの猫

　まず、モデルとしては、シュレーディンガーの猫ではなく、ナンドウの猫を用いる。つまり、アルファ粒子の崩壊のかわりに、回転コインを用いて、その確率で、猫の生死を決める。次のように。

　　　　　□━━━━━━━━━━━Ю

　　　回転コイン検出器　　　　　　　　　　　　猫毒殺の装置

　箱のなかでコインが回転している。ある程度の時間がたつと、コインが倒れて、表か裏かが決まる。
　・表ならば、毒殺装置は働かず、猫は「生」となる。
　・裏ならば、毒殺装置は働いて、猫は「死」となる。

　ただし、コインが倒れた時点では、コインはまだ箱のなかにあり、コインの状態は判明していない。その後、観測者が猫を観測したときに、猫の生死が判明する。

　以上のことは、次の図で説明できる。　（横軸は時間、縦軸は生死。）

回転コインと猫

　この図は、次のことを意味する。

　　　t₀ に実験が開始される。
　　　t₀ からt₁ までの間では、コインは回転しており、裏表は未確定である。
　　　t₁ にコインが倒れる。このとき、裏表が確定する。
　　　５分後に観測がなされる。このとき、裏表が判明する。

　こういう事実を図にすると、上の図になる、と理解してもよい。

　さて。上の図から、次のことがわかる。
　「確定と判明とは、別のことである」

　コインの裏表が確定する時点は、コインが倒れたときである。つまり、t₁ の時点だ。
　一方、観測がなされる時点は、観測者が猫の蓋を開けたときである。つまり、つまり、５分後の時点だ。
　この両者は、別のことである。つまり、確定と判明とは、別のことだ。

　また、「観測が裏表を決定する」ということもない。なぜなら、観測の方が時間的にあとのことだからだ。時間的にあとのことが、過去の事実を決定するとしたら、未来の事象が過去の事象を決定することになるから、相対論に矛盾する。（専用ページで述べたとおり。）

　というわけで、「観測が裏表を決定する」ということはない。裏表は t₁ の時点で決定されている。（確定している。）
　ただし、それが判明するのは、５分後の時点である。
　ここでは、「確定と判明とは別のことだ」と理解しよう。

シュレーディンガーの猫

　シュレーディンガーの猫では、どうだろうか？　ナンドウの猫と同様に、次の図で示せる。

　　　　　□━━━━━━━━━━━Ю

　　　　量子検出器　　　　　　　　　　　　　　　猫毒殺の装置

　箱のなかでアルファ崩壊が起こる。ある程度の時間がたつと、アルファ崩壊が計数管で検出される。検出された時点で、猫毒殺の装置が作動して、猫が死ぬ。

　以上のことは、次の図で説明できる。　（横軸は時間、縦軸は生死。）

アルファ崩壊と猫

　この図は、次のことを意味する。

　　　t₀ に実験が開始される。
　　　５分後に観測がなされる。このとき、猫の生死が判明する。

　さて。この図では、アルファ粒子が崩壊した時点 t₁ は、不明である。 t₁ は、 t₀ から５分後までのどこかの時点であるが、その時点 t₁ が具体的にどの時点かは、わからない。単に「 t₀ から５分後までのどこかだ」とわかるだけだ。

パラドックス

　さて。シュレーディンガーの猫というパラドックスでは、次のことが主張される。　「 t₀ から５分後までの間は、猫の生死が不明である。この期間では、猫は生きているわけでも死んでいるわけでもない。」
　これについて、先の専用ページでは、次のように説明した。
　「このことは、ミクロの世界には成立するが、マクロの世界には成立しない」
　「ミクロの世界では、アルファ粒子の崩壊があるか否かは、どちらにも確定していないが、マクロの世界では、猫の生死がどちらにも確定していないということはない。生死は、どちらかに確定している。人間には判明していないだけだ」
　こう説明することで、マクロの世界のパラドックスは、解決する。これが、先の専用ページで示したことだ。

　では、マクロの世界ではそうであるとして、ミクロの世界では、どうなっているか？　
　これは、確率の問題であるから、ナンドウの猫と同様に考えていい。ただし、確率の変化の仕方が、ナンドウの猫とは少し違う。その違いは、図の形から明らかだろう。
　ただし、もっとよく考えてみよう。つまり、「観測とは何か？」という問題を、よく考える。

ずっと観測する場合

　コペンハーゲン解釈では、次のように主張される。
　「猫の生死は決定されていないが、観測したときに決定される」
　つまり、「猫の生死を決定するのは、観測である」というわけだ。これはいかにも奇妙である。ミクロの世界ではまだしも、マクロの世界では、とうていありえそうにない話だ。

　もちろん、コペンハーゲン解釈は、正しくない。そのことは、常識からわかる。常識的に考えよう。「観測が猫の生死を決定する」というのは、「糸屋の娘が目で殺す」とか、「念力で猫の運命を左右する超能力を働かす」というのと、同様である。
　また、観測が生死を決定するのであれば、この世に殺人犯というものが存在しなくなる。たとえば、ある研究者がシュレーディンガーの猫の毒殺装置で人を殺すことにして、自分は外に出掛けて、アリバイを用意しておく。で、「観測が生死を決定する」のだとすれば、死亡を決定したのは、発見者であって、殺人者ではない。また、死亡時刻には、殺人者にはアリバイがあるから、逮捕されない。（専用ページでおべた通り。）
　こういうのは、あまりにも荒唐無稽だ。

　では、正しくは？　
　実は、「観測」という行為は、事実に何ら影響しないのだ。人間が観測しようが、観測するまいが、装置の全体に対して、何ら影響しない。これは、考えてみれば、当り前のことだ。
　では、このことは、どう説明されるか？　こうだ。

　箱を閉じておくかわりに、ずっと箱を開いておく。最初から最後まで、猫を観測し続ける。この場合、どうなるか？　実は、何も変わらないのだ。
　具体的に示そう。箱を開けたまま、猫をずっと見ているとしよう。５分後に死ぬ確率が50％だとする。猫をずっと見ることにする。
　スタート。１分、２分、３分、……じっと見ていて、４分後に、「死」が観測されたとする。
　この場合、４分後に、猫の死が確定したわけだ。

　では、１分、２分、３分の時点では、どうか？　二通りの解釈が成立する。
　コペンハーゲン解釈では、「観測が生死を確定する」のだから、観測している猫が生きているのであれば、猫は「生」に確定したことになる。ところが、１分、２分、３分の時点では、猫は「生」に確定したはずなのに、４分後または５分後に見たら、猫は死んでいる。「生」が「死」になっている。矛盾。
　私の解釈では、「観測が生死を確定することはない」のだから、観測している猫が生きていても、猫は「生」に確定していない。だから、４分後または５分後に見て、猫は死んでいても、矛盾はない。

　ここで肝心なことは、次のことだ。
　「１分、２分、３分の時点で、その時点の猫を観測していても、５分後の猫の生死については、何ら影響しない」
　つまり、１分、２分、３分の時点で観測されるのは、その時点の猫であって、５分後の猫ではない。昔の武士は、「朝に生きていても、夕べに生きている保証はない」と考えた。それと同様だ。１分、２分、３分の時点で「生」が観測されても、そのことは５分後の「生」とは何の関係もない。１分、２分、３分の時点では、「生」が観測されたとしても（あるいは何も観測されないとしても）、生死は未確定なのだ。

　とにかく、「観測したから猫の生死が決定した」ということはない。３分後に観測しようが観測するまいが、「５分後の猫」の状態はずっと未確定だったのだ。
　そして、「５分後の猫」の状態を確定させたものは、５分後の観測ではない。時刻ｔにおいて観測しようが観測するまいが、「時刻ｔにおける猫の状態」は、時刻ｔになったときに自動的に決まる。
　たとえば、時刻ｔにおけるあなたの生死は、誰かが観測しようがするまいが、ちゃんと決まる。
　同様に、この世界から人間がすべて消滅して、シュレーディンガーの猫という一匹だけがいたとしよう。その場合、誰も観測しないとしても、時刻ｔにおける猫の生死は、ちゃんと確定している。「人が誰も観測していないので、あたしの生死はあたしにもわからない」と猫が思うことは、ありえない。

（ ※　なお、「生」が観測されたのではなく、「死」が観測された場合には、死が確定する。この片方向性が、話をごちゃごちゃにして、混乱を招く。このことは、あとで別に考えることにして、今は「生」の場合だけを考えておく。）

観測後の死

　では、５分後まで「生」が観測されたとしよう。その場合、猫の「生」が確定するだろうか？　
　５分後に箱を開けた時点で、猫が生きていたとする。ただし、観測した一瞬後に、アルファ粒子が崩壊して、猫が死んでしまった、とする。
　このことを、どう理解するか？

　観測したときには「生」であるが、その一瞬あとでは、猫は「死」である。観測と現実とが矛盾する。これは、まずい。
　では、どうするべきか？　この食い違いを防ぐために、次の措置を取ればよい。
　「観測と同時に、猫毒殺装置の電源を切る」

　この措置を取れば、大丈夫。もはや、食い違いはなくなる。
　ただし、この場合、猫の生死を決定するのは、観測ではなくて、「電源を切る」という行為である。この行為が、「猫をもはや死なせない」という意味で、生死を決定する。

　ただし、この行為（毒殺装置の解除）は、全面的に決定的ではなく、半面的に決定的であるだけだ。つまり、「未来の死を遮断する」ことはできるが、「未来の生を遮断する」ことはできない。また、「未来の死を遮断する」ことはできるが、「過去の死を遮断する」ことはできない。（いったん死んだ猫を生き返らせることはできない。）

コペンハーゲン解釈の誤解

　ここまで考えると、「観測した瞬間に、生死が収束する」というコペンハーゲン解釈には、次の誤解があることに気づく。

　(1)
　「生」が観測されても、そのことは、「生の決定」ないし「生の確定」を意味しない。
　箱を開けた時点よりも前であれば、観測は生死（５分後の猫の生死）には、影響しない。単に、その時点より前の猫の「生」を見ているだけだ。（３分後の猫は、５分後の猫とは違う。）
　箱を開けた時点よりも後であれば、観測は生死（５分後よりもあとの猫の生死）には、影響しない。５分後よりもあとの猫の生死を決めるのは、猫毒殺装置のＯＮ・ＯＦＦであって、観測ではない。

　(2)
　「死」が観測されても、そのことは、「死の決定」ないし「死の確定」を意味しない。
　箱を開けた時点よりも前であれば、猫が死んだ時点で、観測している。たとえば、３分後に死んだとき、まさしく３分後に観測している。しかしそれは、「観測が死を決定した」ということにはならない。理由は、二つ。
　第１に、１分後にも、２分後にも、ずっと観測していたが、猫は死ななかった。観測したから死んだわけではない。
　第２に、ずっと観測し続けている人がいても、猫は必ずしも死なない。たくさんの人が同じように観測すれば、半数の人が「死」を観測し、半数の人が「死」を観測しない。……だったら、「観測が死を決定した」ということは、成立しない。（半分しか当たらない命題は真ではない。その命題は、真ではないから、偽である。）

　以上の (1) (2) から、こうわかる。
　「観測は、猫の生死に、何も影響しない。背後でこっそり毒殺装置をＯＦＦにしたのを無視したり、たまたま半数の人間にだけ適用されるのを誤解したり、そういう勘違いがあるだけだ。」

観測の意味

　では、「観測が生死を決定する」のでなければ、正しくは、どうなのか？

　まず、マクロの世界では、こう言える。
　「観測は、猫の生死に、何も影響しない。観測したときに起こるのは、観測者にとっての『判明』だけである。その意味は、何らかの関数が一瞬にして変化することではなくて、観測者の思考対象が『頭のなかの猫』から『現実の猫』に切り替わったことだ。」
　この件は、詳しくは、先の専用ページで説明した。そちらを参照。

　では、（マクロの世界でなく）ミクロの世界では、どうなのか？　
　この件は、「量子力学とは何か？」という大問題に直結する。直結させたあとで、簡単に結論だけを書けば、こうなる。

　「観測が（ミクロの）状態を決定するのではない。状態が決定されるということは、波が粒子になるということだ。波が粒子になったとき、観測されなかったものが観測される。」
　つまり、こうだ。
　「観測が状態を決めるのではない。状態が観測を決めるのでもない。状態が『観測可能かどうか』を決める」
　波の状態では、観測が不可能だ。粒子の状態では、観測が可能だ。そこで、波が粒子になったとき、観測者は初めて、観測する。そして、こう思う。
　「おれが観測したから、波が粒子になったのだ。何しろ、おれが観測するまでは、波は粒子になっていなかったのだからな」

　これは、とんでもない勘違いだ。人が観測したから、そこに粒子が出現したのではない。そこに粒子が出現したから、人が観測することが可能になったのだ。
　たとえて言おう。炭酸ガスを冷やして、ドライアイスにする。人が観測していると、だんだんと、何もない空間にドライアイスが現れる。これを、どう解釈するか？
　コペンハーゲン解釈では、こうなる。
　「おれが観測したから、炭酸ガスがドライアイスになったのだ。おれが見るまではずっと未確定だったが、おれが見た瞬間に、炭酸ガスが一瞬にしてドライアイスになったのだ。観測が状態を決定するのだ。」
　私の解釈では、こうなる。
　「炭酸ガスがドライアイスになった。それだけのことだ。ドライアイスは、固体になったから、観測が可能になった。観測が可能になったから、実際に観測しただけだ。ここでは、人が観測しようがしまいが、ドライアイスはちゃんと存在する。観測は状態にまったく影響しない。」

　というわけで、「観測する」ということと、「観測可能だ」ということとを、はっきりと区別するべきなのだ。この両者を区別しないと、混同して、話が混乱する。

　もう少し正確に言おう。「観測する」という言葉は、次の二つを意味する。
　 (i) 人間が目を向ける
　 (ii) 対象が感覚器で知覚されて、それが脳で認識される。
　今までの通常の解釈では、この (i)(ii) をごちゃ混ぜにして理解している。そのせいで、奇妙な結論が出てしまうのだ。しかし、この二つを区別すれば、次のように言える。
　「(i) が成立したからといって、(ii) が成立するとは限らない」
　「人間が目を向けたからといって、対象が脳で認識されるとは限らない」
　人間がずっと目を向けていたとしよう。あるとき突然、目の前に、粒子が出現する。なぜか？　そのとき、粒子がそこに出現したからだ。つまり、そこにおいて「波　→　粒子」という転換が起こったからだ。つまり、量子が「観測可能」になったからだ。……こう理解すれば、何も問題はない。
　しかし、「人が観測したから、粒子が出現したのだ」というような発想では、(i)(ii) をごちゃ混ぜにして理解している。そのせいで、「人が目を向けたから、粒子が出現したのだ」というような結論が出てしまう。
　要するに、「観測する」という言葉を、いい加減に使っているから、おかしな混乱が生じるのだ。
　こういう混乱が、シュレーディンガーの猫のパラドックスだ。

　概念がこんぐらがると、論理がこんぐらがって、パラドックスが生じる。それだけのことだ。……もつれているのは、現実ではなくて、その解釈（コペンハーゲン解釈）だけだ。そんなもつれた解釈は、さっさと捨ててしまえばよい。そしてかわりに、「観測する」ということと、「観測可能だ」ということとを、はっきりと区別すること［つまり (i)(ii) を区別すること］によって、現実を正しく理解すればよい。

　そして、「観測する」ということと、「観測可能だ」ということとを、はっきりと区別するためにあるのが、「波と粒子との、相互転換」という発想だ。この発想を詳しく説明するのが、「二重スリット」の理論だ。

　※　というわけで、あとは、「二重スリット」のページを読んでほしい。
　※　ただしその前に、「物理学における問題」のページも読むといいだろう。
　※　本論で述べた理論の実験的な裏付けについては、次の付録を参照。

　【付録】

　　　カシミール効果とコペンハーゲン解釈

　カシミール効果（ Casimir Effect ）と呼ばれる現象が観測されている。この現象は、1997年に、実験的にはっきりと検証された。
　カシミール効果は、コペンハーゲン解釈が正しくない、ということをはっきりと示す。大略を言えば、次の通り。

　コペンハーゲン解釈では、観測が状態を決める。つまり、観測するまでは、（波動関数による）値が定まらない。そして、観測した瞬間に、値が決まる。
　ところが、カシミール効果の実験では、次のことが判明している。
　「真空中の電子の存在確率はゼロである。ところが、存在確率はゼロでも、電子と反電子のペアが、たえず発生したり消滅したりしている。」
　これはつまり、（値の）「未確定」の状態と「確定」の状態とが、相互に転換している、ということだ。
　図示すれば、次のようになる。

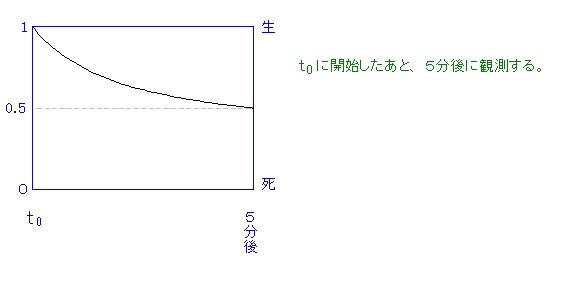
コペンハーゲン解釈（観測前）	（観測後）　　　　　 or 　　 or 　無
カシミール効果　　　　　無　←→　　＋	（確定後）　　　　　 or 　　 or 　無

　コペンハーゲン解釈では、黒丸または白丸が存在するのは、観測後だけのはずだ。観測前には、黒丸も白丸も存在しないはずだ。
　ところが、カシミール効果の実験によれば、観測前にも、黒丸および白丸が存在していることがある。（表の左下の欄。）
　ただし、黒丸および白丸が存在するときには、次の条件がある。
　・黒丸と白丸はペア（一対）で存在する。（平均すれば灰色）
　・無［＝真空＝灰色］の状態では、粒子になっていない。
　この二つがどういうことを意味するかは、別の箇所で説明する。（後述のリンクを参照。）
　ただ、正解が何であるかは別として、コペンハーゲン解釈が正しくないことは、カシミール効果によって判明したことになる。

　わかりやすく言おう。二重スリットの実験で、スリットのところに電子があるかどうか？　コペンハーゲン解釈では、こう答える。
　「光を当てて観測するまでは、スリットには電子が存在しない。光を当てて観測した瞬間に、どちらか一方のスリットに電子が見出される。」
　しかし、カシミール効果の実験からは、正解は次のようになる。
　「観測しようがしまいが、スリットではたえず、電子と反電子が発生したり消滅したりしている。たとえ人間が観測しなくても、スリットには電子が存在することがあるのだ。（ただし、反電子をともなうが。なお、その電子が、反電子とペアになる電子か、電子銃から発射された電子であるかは、区別不能である。）」
　こうして、コペンハーゲン解釈は、実験事実によって否定される。なぜなら、存在しないはずのものが存在するのだから。結局、コペンハーゲン解釈は、間違っていることが、はっきりと実験的に証明されたのだ。これは重要な結論だ。

（ ※　なお、正解が何であるかは、次の箇所で説明する。 →　「物理学における問題」の［付録］）
（ ※　カシミール効果が物理学においてどういう意義をもつかは、次のページで説明している。　→　「カシミール効果の重要性」）

　この箇所にあった　【波動関数の収束とＥＰＲパラドックス】　という説明は、次の箇所に移転した。
　　→　細々とした周辺的な話題　（該当箇所）

　　関連ページ

　　このページについて

　　　　氏　名　　　南堂久史
　　　　メール　　　nando@js2.so-net.ne.jp
　　　　ＵＲＬ　　　http://hp.vector.co.jp/authors/VA011700/physics/observe.htm　（本ページ）

[ THE END ]　　　　

　