�x�N�g�����
< �ڎ��� >
�P�D�x�N�g���̒�`
 �ψʁA���x�A�����x�A�͂Ȃǂ̗l�ɑ傫���ƕ�����L����ʂ��x�N�g���i�u�d�b�s�n�q�j�Ƃ����A���ʁA���x�A�G�l���M�[�Ȃǂ̗l�ɑ傫���݂̂�L����ʂ��X�J���[�i�r�b�`�k�`�q�j�Ƃ����B�x�N�g���͖��̂���������
�ψʁA���x�A�����x�A�͂Ȃǂ̗l�ɑ傫���ƕ�����L����ʂ��x�N�g���i�u�d�b�s�n�q�j�Ƃ����A���ʁA���x�A�G�l���M�[�Ȃǂ̗l�ɑ傫���݂̂�L����ʂ��X�J���[�i�r�b�`�k�`�q�j�Ƃ����B�x�N�g���͖��̂���������  �ƕ\���B��̍����n���n�_�Ƃ����A��̐�`���I�_�Ƃ����B�����̌����̓x�N�g���̌����������A���̒����͑傫���������B�ȒP�Ɉ�̕����ŕ\���ɂ�
�ƕ\���B��̍����n���n�_�Ƃ����A��̐�`���I�_�Ƃ����B�����̌����̓x�N�g���̌����������A���̒����͑傫���������B�ȒP�Ɉ�̕����ŕ\���ɂ� �ƕ\���B��̃x�N�g��
�ƕ\���B��̃x�N�g��  ��
��  �Ƃ̑傫���ƕ��������ɓ��������́A�����̎n�_�̔@���Ɋւ�炸
�Ƃ̑傫���ƕ��������ɓ��������́A�����̎n�_�̔@���Ɋւ�炸  ��
��  �͑��������Ƃ����B
�͑��������Ƃ����B
(1) ���x�N�g��
�����Ȃ�n�ɂ����̐����Œ�`�������ʂȂS�̃x�N�g���i�����x�N�g���j������B
�@�@�@(1,0,0,0)�@�@(0,1,0,0)�@�@(0,0,1,0)�@�@(0,0,0,1)
�@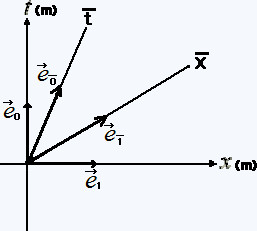
�nS�ɉ�������x�N�g���� �C
�C �C
�C �C
�C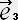
�n �ɉ�������x�N�g����
�ɉ�������x�N�g����  �C
�C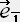 �C
�C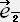 �C
�C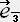
�Ƃ��ꂼ��\���B
�Y���͉��t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB
�@

�nS�ɉ�������x�N�g����
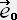 �C
�C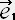 �C
�C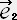 �C
�C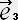
�n
 �ɉ�������x�N�g����
�ɉ�������x�N�g����  �C
�C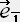 �C
�C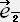 �C
�C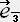
�Ƃ��ꂼ��\���B
�Y���͉��t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB
(2) ��ʂ̃x�N�g��
�nS�ɉ������ʂ̃x�N�g����  ���i
���i �C
�C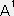 �C
�C �C
�C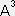 �j
�j
 �C
�C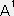 �C
�C �C
�C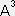 �͌nS�ɉ����鐬���B���x�N�g����p���ĕ\���Ɓi�Y���͏�t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB�j
�͌nS�ɉ����鐬���B���x�N�g����p���ĕ\���Ɓi�Y���͏�t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB�j
�@�@�@���@ ��
��
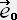 �{
�{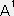
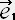 �{
�{
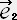 �{
�{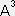
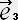
�n �ɉ������ʂ̃x�N�g����
�ɉ������ʂ̃x�N�g����  ���i
���i �C
�C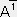 �C
�C �C
�C �j
�j
 �C
�C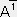 �C
�C �C
�C �͌n
�͌n �ɉ����鐬���B���x�N�g����p���ĕ\����
�ɉ����鐬���B���x�N�g����p���ĕ\����
�@�@�@���@ ��
��
 �{
�{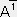
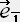 �{
�{
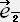 �{
�{
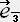
 ���i
���i �C
�C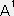 �C
�C �C
�C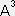 �j
�j �C
�C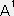 �C
�C �C
�C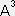 �͌nS�ɉ����鐬���B���x�N�g����p���ĕ\���Ɓi�Y���͏�t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB�j
�͌nS�ɉ����鐬���B���x�N�g����p���ĕ\���Ɓi�Y���͏�t���Ƃ���B�ڍׂ� �W�D���ρA���σx�N�g���ƓY���̈ʒu���Q�ƁB�j ��
��
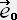 �{
�{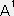
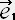 �{
�{
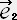 �{
�{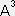
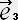
 �ɉ������ʂ̃x�N�g����
�ɉ������ʂ̃x�N�g����  ���i
���i �C
�C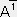 �C
�C �C
�C �j
�j �C
�C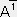 �C
�C �C
�C �͌n
�͌n �ɉ����鐬���B���x�N�g����p���ĕ\����
�ɉ����鐬���B���x�N�g����p���ĕ\���� ��
��
 �{
�{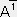
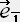 �{
�{
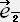 �{
�{
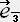
�Q�D�x�N�g���̑㐔
(1) �x�N�g���̐����̕ϊ�
�nS�ɉ�������W�l�̓��[�����c�ϊ��ɂ��n �̍��W�l�ɕϊ��o�����B���l�Ƀx�N�g���̐��������[�����c�ϊ��ɂ��ϊ��o����B�������[�����c�ϊ��s��
�̍��W�l�ɕϊ��o�����B���l�Ƀx�N�g���̐��������[�����c�ϊ��ɂ��ϊ��o����B�������[�����c�ϊ��s�� 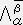 ��p���āi ��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ��s���p���Ă���B
�i���ꑊ�Θ_����@�t�^�F��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ����Q�ƁB�@�ȒP�Ȍ`�̃��[�����c�ϊ��s������ꑊ�Θ_����@2. �K�����C�ϊ��ƃ��[�����c�ϊ����Q�� �j �j
��p���āi ��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ��s���p���Ă���B
�i���ꑊ�Θ_����@�t�^�F��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ����Q�ƁB�@�ȒP�Ȍ`�̃��[�����c�ϊ��s������ꑊ�Θ_����@2. �K�����C�ϊ��ƃ��[�����c�ϊ����Q�� �j �j

 ���A�C���V���^�C���̑��a�̋K����p���ď�����
���A�C���V���^�C���̑��a�̋K����p���ď�����
�@�@�@�@�@ ��
��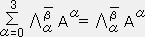 �@�@�@�@�@�@�@�@�@�i
�@�@�@�@�@�@�@�@�@�i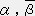 ���O�`�R�j
���O�`�R�j
 �̍��W�l�ɕϊ��o�����B���l�Ƀx�N�g���̐��������[�����c�ϊ��ɂ��ϊ��o����B�������[�����c�ϊ��s��
�̍��W�l�ɕϊ��o�����B���l�Ƀx�N�g���̐��������[�����c�ϊ��ɂ��ϊ��o����B�������[�����c�ϊ��s�� 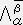 ��p���āi ��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ��s���p���Ă���B
�i���ꑊ�Θ_����@�t�^�F��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ����Q�ƁB�@�ȒP�Ȍ`�̃��[�����c�ϊ��s������ꑊ�Θ_����@2. �K�����C�ϊ��ƃ��[�����c�ϊ����Q�� �j �j
��p���āi ��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ��s���p���Ă���B
�i���ꑊ�Θ_����@�t�^�F��Ԏ�����]���Ă��鎞�̃��[�����c�ϊ����Q�ƁB�@�ȒP�Ȍ`�̃��[�����c�ϊ��s������ꑊ�Θ_����@2. �K�����C�ϊ��ƃ��[�����c�ϊ����Q�� �j �j
 ���A�C���V���^�C���̑��a�̋K����p���ď�����
���A�C���V���^�C���̑��a�̋K����p���ď����� ��
��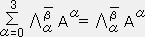 �@�@�@�@�@�@�@�@�@�i
�@�@�@�@�@�@�@�@�@�i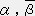 ���O�`�R�j
���O�`�R�j
�y�A�C���V���^�C���̑��a�̋K��z
��̓Y������t���ŁA����Ɠ����Y�������t���ŏo�Ă��鎮�ł͏�ɂ��̓Y���̎�肤��l���ׂĂɂ��Ă̑��a����鎖�ł���B�i ���a�̋L�� �� ���ȗ�����B �j
�@�@�@�@�@ ��
�� �@�@�@�i
�@�@�@�i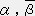 ���O�`�R�j
���O�`�R�j
�@�@�@�@�@ ��
��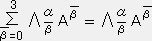 �@�@�@�@�@�i
�@�@�@�@�@�i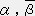 ���O�`�R�j�@�E�E�E�E�E�@�i�P�j
���O�`�R�j�@�E�E�E�E�E�@�i�P�j
�M���V�������̓Y���͂O�`�R�̒l�����A���[�}���̓Y���͂P�`�R�̒l�����B
�@�@�@���@A��P����A�OP�O�{A�PP�P�{A�QP�Q�{A�RP�R�@�@�C�@�@A��P����A�PP�P�{A�QP�Q�{A�RP�R
���@�[�iA0�j2+�iA1�j2+�iA2�j2+�iA3�j2���[�i �j2+�i
�j2+�i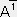 �j2+�i
�j2+�i �j2+�i
�j2+�i �j2�@�ƂȂ���ꑊ�Θ_����ŏq�ׂ��Ԋu�̕s�ϐ�������B
�j2�@�ƂȂ���ꑊ�Θ_����ŏq�ׂ��Ԋu�̕s�ϐ�������B
�@�@�@�@�@
 ��
�� �@�@�@�i
�@�@�@�i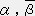 ���O�`�R�j
���O�`�R�j�@�@�@�@�@
 ��
��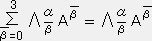 �@�@�@�@�@�i
�@�@�@�@�@�i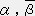 ���O�`�R�j�@�E�E�E�E�E�@�i�P�j
���O�`�R�j�@�E�E�E�E�E�@�i�P�j�@�@�@���@A��P����A�OP�O�{A�PP�P�{A�QP�Q�{A�RP�R�@�@�C�@�@A��P����A�PP�P�{A�QP�Q�{A�RP�R
 �j2+�i
�j2+�i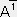 �j2+�i
�j2+�i �j2+�i
�j2+�i �j2�@�ƂȂ���ꑊ�Θ_����ŏq�ׂ��Ԋu�̕s�ϐ�������B
�j2�@�ƂȂ���ꑊ�Θ_����ŏq�ׂ��Ԋu�̕s�ϐ�������B
�E�@ �͒萔�ɂ����Ȃ����Ƃ���
�͒萔�ɂ����Ȃ����Ƃ���
�@�@�@�@�@ ����
���� �^��A��
�^��A��
�E�@������\���L�@�����̗l�ɒ�߂�B
�@�@�@�@�@�݃��^��X�����Cx�@�@�@�@�݃��^��X�������C�� �@�@�@�@��X���^��X����X���C��
�E�@�_�~�[�̓Y���ƃt���[�̓Y���ɂ���
�@�@�@���a��\���ׂɎg�p�����Y�����_�~�[�̓Y���Ƃ����A�a���Ƃ�Ȃ��Y�����t���[�̓Y���Ƃ����B
�@�@�@�i�P�j�̎��ɉ����� �� �̓_�~�[�̓Y���ŁA �� �̓t���[�̓Y���ł���B�_�~�[�̓Y�����t���[�̓Y����
�@�@�@�ǂ�ȕ������g�p���Ă��\��Ȃ����A�t���[�̓Y����t�������鎞�͑S�Ă�t�������Ȃ���Ȃ�Ȃ��B
�@�@�@���̎��́i�P�j�̎��Ɠ����ł���B
�@�@�@�@�@�@�@�`�������� ���`��
 �͒萔�ɂ����Ȃ����Ƃ���
�͒萔�ɂ����Ȃ����Ƃ����@�@�@�@�@
 ����
���� �^��A��
�^��A���E�@������\���L�@�����̗l�ɒ�߂�B
�@�@�@�@�@�݃��^��X�����Cx�@�@�@�@�݃��^��X�������C�� �@�@�@�@��X���^��X����X���C��
�E�@�_�~�[�̓Y���ƃt���[�̓Y���ɂ���
�@�@�@���a��\���ׂɎg�p�����Y�����_�~�[�̓Y���Ƃ����A�a���Ƃ�Ȃ��Y�����t���[�̓Y���Ƃ����B
�@�@�@�i�P�j�̎��ɉ����� �� �̓_�~�[�̓Y���ŁA �� �̓t���[�̓Y���ł���B�_�~�[�̓Y�����t���[�̓Y����
�@�@�@�ǂ�ȕ������g�p���Ă��\��Ȃ����A�t���[�̓Y����t�������鎞�͑S�Ă�t�������Ȃ���Ȃ�Ȃ��B
�@�@�@���̎��́i�P�j�̎��Ɠ����ł���B
�@�@�@�@�@�@�@�`�������� ���`��
(2) ���x�N�g���̕ϊ�
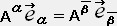 �@�Ɓ@
�@�Ɓ@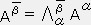 �@���@
�@���@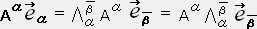
�]���ā@
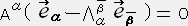 �@�@
�@�@ �@�͔C�ӂȂ̂�
�@�͔C�ӂȂ̂��@�@�@���@
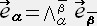
���x�N�g���̕ϊ��͐����̕ϊ��ł͂Ȃ��A�nS�̊��
 ���n
���n �ł̊��
�ł̊�� 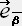 �̐��`�����ŕ\���������̂ł���B
�̐��`�����ŕ\���������̂ł���B�t�ϊ��i
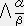 ��p���Ă̕ϊ��j�͏�L�̕��@�Ɠ��l�ȕ��@�ŋ��߂��
��p���Ă̕ϊ��j�͏�L�̕��@�Ɠ��l�ȕ��@�ŋ��߂���@�@�@���@
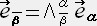 �ƂȂ�B
�ƂȂ�B(3) �ϊ��s��̐�
�nS����n �ւ̕ϊ��s��
�ւ̕ϊ��s�� 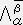 �ƌn
�ƌn ����nS�ւ̕ϊ��s��
����nS�ւ̕ϊ��s��  �Ƃ̐ς͎��̗l�ɂȂ�B
�Ƃ̐ς͎��̗l�ɂȂ�B
�@�@�@���@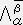
 ���������@�@�@�@�̓N���l�b�J�[�̃f���^
���������@�@�@�@�̓N���l�b�J�[�̃f���^
���̎�����s��  ��
�� 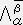 �̋t�s��ł��鎖���킩��B
�̋t�s��ł��鎖���킩��B
 �ւ̕ϊ��s��
�ւ̕ϊ��s�� 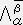 �ƌn
�ƌn ����nS�ւ̕ϊ��s��
����nS�ւ̕ϊ��s��  �Ƃ̐ς͎��̗l�ɂȂ�B
�Ƃ̐ς͎��̗l�ɂȂ�B�@�@�@���@
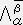
 ���������@�@�@�@�̓N���l�b�J�[�̃f���^
���������@�@�@�@�̓N���l�b�J�[�̃f���^ ��
�� 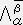 �̋t�s��ł��鎖���킩��B
�̋t�s��ł��鎖���킩��B
(4) �ϊ��̋�̗�
�n  �̊��
�̊�� 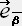 ���nS�ł̊��
���nS�ł̊��  �ŕ\�������
�ŕ\�������

 �� ��
�� �� 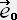 �@+�� Vx
�@+�� Vx 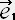 �@+�� Vy
�@+�� Vy 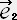 �@+�� Vz
�@+�� Vz 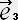 �@�@�@
( �� ��
�@�@�@
( �� ��  )
)
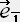 �� �� Vx
�� �� Vx 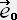 �@+(1+(�� -1)Vx 2/V2)
�@+(1+(�� -1)Vx 2/V2) 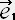 �@+((�� -1)VxVy/V2)
�@+((�� -1)VxVy/V2)
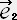 �@+((�� -1)VxVz/V2)
�@+((�� -1)VxVz/V2)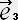
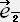 �� �� Vy
�� �� Vy 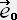 �@+((�� -1)VxVy/V2)
�@+((�� -1)VxVy/V2)
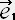 �@+(1+(�� -1)Vy 2/V2)
�@+(1+(�� -1)Vy 2/V2) 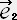 �@+((�� -1)VyVz/V2)
�@+((�� -1)VyVz/V2)
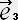
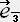 �� �� Vz
�� �� Vz 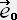 �@+((�� -1)VxVz/V2)
�@+((�� -1)VxVz/V2)
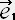 �@+((�� -1)VyVz/V2)
�@+((�� -1)VyVz/V2)
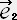 �@+(1+(�� -1)Vz 2/V2)
�@+(1+(�� -1)Vz 2/V2) 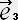 �x�N�g��
�x�N�g�� �̌nS�ł̐������i�U�C�R�C�P�C�S�j�Ƃ���ƌn
�̌nS�ł̐������i�U�C�R�C�P�C�S�j�Ƃ���ƌn �ł̐����i
�ł̐����i �C
�C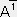 �C
�C �C
�C �j��
�@�@�@
�j��
�@�@�@ �@�@�@�@
�@�@�@�@ �� �U��-�R��Vx-��Vy�|�S��Vz
�� �U��-�R��Vx-��Vy�|�S��Vz
�@�@�@�@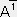 ��-�U��Vx+�R+�R(��-1) Vx2/V2+(��-1) VxVy/V2+�S(��-1) VxVz/V2
��-�U��Vx+�R+�R(��-1) Vx2/V2+(��-1) VxVy/V2+�S(��-1) VxVz/V2
�@�@�@�@ ��-�U��Vy+�R(��-1) VxVy/V2+�P+(��-1)Vy2/V2+�S(��-1)VyVz/V2
��-�U��Vy+�R(��-1) VxVy/V2+�P+(��-1)Vy2/V2+�S(��-1)VyVz/V2
�@�@�@�@ ��-�U��Vz+�R(��-1)VxVz/V2+(��-1)VyVz/V2+�S+�S(��-1)Vz2/V2
��-�U��Vz+�R(��-1)VxVz/V2+(��-1)VyVz/V2+�S+�S(��-1)Vz2/V2
 �̊��
�̊�� 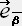 ���nS�ł̊��
���nS�ł̊��  �ŕ\�������
�ŕ\�������
 �� ��
�� �� 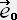 �@+�� Vx
�@+�� Vx 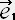 �@+�� Vy
�@+�� Vy 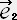 �@+�� Vz
�@+�� Vz 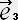 �@�@�@
( �� ��
�@�@�@
( �� ��  )
)
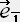 �� �� Vx
�� �� Vx 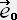 �@+(1+(�� -1)Vx 2/V2)
�@+(1+(�� -1)Vx 2/V2) 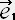 �@+((�� -1)VxVy/V2)
�@+((�� -1)VxVy/V2)
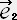 �@+((�� -1)VxVz/V2)
�@+((�� -1)VxVz/V2)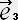
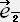 �� �� Vy
�� �� Vy 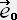 �@+((�� -1)VxVy/V2)
�@+((�� -1)VxVy/V2)
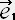 �@+(1+(�� -1)Vy 2/V2)
�@+(1+(�� -1)Vy 2/V2) 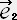 �@+((�� -1)VyVz/V2)
�@+((�� -1)VyVz/V2)
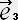
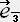 �� �� Vz
�� �� Vz 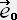 �@+((�� -1)VxVz/V2)
�@+((�� -1)VxVz/V2)
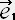 �@+((�� -1)VyVz/V2)
�@+((�� -1)VyVz/V2)
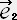 �@+(1+(�� -1)Vz 2/V2)
�@+(1+(�� -1)Vz 2/V2) 
 �̌nS�ł̐������i�U�C�R�C�P�C�S�j�Ƃ���ƌn
�̌nS�ł̐������i�U�C�R�C�P�C�S�j�Ƃ���ƌn �ł̐����i
�ł̐����i �C
�C �C
�C �C
�C �j��
�j��

 �� �U��-�R��Vx-��Vy�|�S��Vz
�� �U��-�R��Vx-��Vy�|�S��Vz�@�@�@�@
 ��-�U��Vx+�R+�R(��-1) Vx2/V2+(��-1) VxVy/V2+�S(��-1) VxVz/V2
��-�U��Vx+�R+�R(��-1) Vx2/V2+(��-1) VxVy/V2+�S(��-1) VxVz/V2�@�@�@�@
 ��-�U��Vy+�R(��-1) VxVy/V2+�P+(��-1)Vy2/V2+�S(��-1)VyVz/V2
��-�U��Vy+�R(��-1) VxVy/V2+�P+(��-1)Vy2/V2+�S(��-1)VyVz/V2�@�@�@�@
 ��-�U��Vz+�R(��-1)VxVz/V2+(��-1)VyVz/V2+�S+�S(��-1)Vz2/V2
��-�U��Vz+�R(��-1)VxVz/V2+(��-1)VyVz/V2+�S+�S(��-1)Vz2/V2
�R�D�l�����x
�K�����I�̎O�����w�ł͑��x�͗��q�̋O���ɐڂ���x�N�g���ł���B�ڃx�N�g���̐������w�i���j,�x�i���j,�y�i���j�@�@�O�����x���u��,�u��,�u���Ƃ����
�@�@�@�@�@�u��=�����^����,�@�u��=�����^����,�@�u��=�����^����

�~���R�t�X�L�[�̎���}�ɉ�����l�����w�ł͑��x�͗��q�̐��E���ɐڂ���x�N�g���ł���A�ڃx�N�g�� 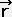 �̐������ŗL�����т̊��Ƃ��ĕ\�����B�l�����x
�̐������ŗL�����т̊��Ƃ��ĕ\�����B�l�����x  �̌nS�ɉ����鐬�����t��,�t��,�t��,�t���Ƃ����
�̌nS�ɉ����鐬�����t��,�t��,�t��,�t���Ƃ����
�@�@�@�t���������^����,�@�t�������w�^����,�@�t�������x�^����,�@�t�������y�^����
���Ԃ̒x��ɂ�� ���с� ���� �̊W������̂�
���� �̊W������̂�
�@�@���@�t���� ,�@�t����
,�@�t���� �u��,�@�t����
�u��,�@�t���� �u��,�@�t����
�u��,�@�t���� �u��
�u��
�t��,�t��,�t��,�t�������[�����c�ϊ��s�� 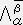 �ɂ��ϊ����A
�ɂ��ϊ����A �̐����ŕ\���Ɓi�P�C�O�C�O�C�O�j�ƂȂ�B����͌n
�̐����ŕ\���Ɓi�P�C�O�C�O�C�O�j�ƂȂ�B����͌n �ɉ�������x�N�g��
�ɉ�������x�N�g��  �ł���B�]���Ĉ�l�ȉ^�������Ă��闱�q�̎l�����x���A���̗��q�̐Î~�n�ł̃x�N�g��
�ł���B�]���Ĉ�l�ȉ^�������Ă��闱�q�̎l�����x���A���̗��q�̐Î~�n�ł̃x�N�g��  �Ƃ��Ē�`���鎖���\�ł���B
�Ƃ��Ē�`���鎖���\�ł���B
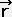 �̐������ŗL�����т̊��Ƃ��ĕ\�����B�l�����x
�̐������ŗL�����т̊��Ƃ��ĕ\�����B�l�����x  �̌nS�ɉ����鐬�����t��,�t��,�t��,�t���Ƃ����
�̌nS�ɉ����鐬�����t��,�t��,�t��,�t���Ƃ���� ���� �̊W������̂�
���� �̊W������̂� ,�@�t����
,�@�t���� �u��,�@�t����
�u��,�@�t���� �u��,�@�t����
�u��,�@�t���� �u��
�u��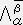 �ɂ��ϊ����A
�ɂ��ϊ����A �̐����ŕ\���Ɓi�P�C�O�C�O�C�O�j�ƂȂ�B����͌n
�̐����ŕ\���Ɓi�P�C�O�C�O�C�O�j�ƂȂ�B����͌n �ɉ�������x�N�g��
�ɉ�������x�N�g��  �ł���B�]���Ĉ�l�ȉ^�������Ă��闱�q�̎l�����x���A���̗��q�̐Î~�n�ł̃x�N�g��
�ł���B�]���Ĉ�l�ȉ^�������Ă��闱�q�̎l�����x���A���̗��q�̐Î~�n�ł̃x�N�g��  �Ƃ��Ē�`���鎖���\�ł���B
�Ƃ��Ē�`���鎖���\�ł���B
�S�D�l���^����
�l���^���� 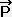 ��
�� 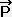 ����
���� �i �Î~���� �� �l�����x �j �Ƃ��Ē�`�����B�nS�ɉ����鐬����
�i �Î~���� �� �l�����x �j �Ƃ��Ē�`�����B�nS�ɉ����鐬���� 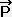 ���i ��0�C��1�C��2�C��3 �j �Ƃ����
���i ��0�C��1�C��2�C��3 �j �Ƃ����
�@�@�@���@��0��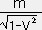 , �@��1��
, �@��1��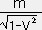 �u�� , �@��2��
�u�� , �@��2��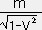 �u�� , �@��3��
�u�� , �@��3��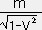 �u��
�u��
��0�̓G�l���M�[�i���d�@�ؖ��͉��L�Q�Ɓj�ł���B��L�̎��̊W����d2����2�{�i��1�j2�{�i��2�j2�{�i��3�j2�ł��鎖��������B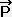 �̌n
�̌n �ɉ����鐬���́i���C�O�C�O�C�O�j�ł���B
�ɉ����鐬���́i���C�O�C�O�C�O�j�ł���B
 ��藝�œW�J����� �P�{�u2�^�Q�{�R�u4�^�i�Sx�Q�I�j�{�E�E�E�@�@�Ȃ̂łu�����������G�l���M�[��
��藝�œW�J����� �P�{�u2�^�Q�{�R�u4�^�i�Sx�Q�I�j�{�E�E�E�@�@�Ȃ̂łu�����������G�l���M�[��
�@�@�@�@�@�d�����{���u2�^�Q
��Q���̓j���[�g���͊w�ɉ�����^���G�l���M�[�ŁA��P���͐Î~�G�l���M�[�ł���B�Î~���Ă�����̂����̎��ʂ̂��߂ɃG�l���M�[�������Ă���B���ʂƃG�l���M�[�Ƃ͓����Ȃ̂ł���B�Î~�G�l���M�[���܂߂ăG�l���M�[�ۑ��̖@�������藧�B
�y ��0 �i���d�j�̓G�l���M�[�ł��� �z
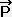 ��
�� 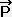 ����
���� �i �Î~���� �� �l�����x �j �Ƃ��Ē�`�����B�nS�ɉ����鐬����
�i �Î~���� �� �l�����x �j �Ƃ��Ē�`�����B�nS�ɉ����鐬���� 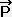 ���i ��0�C��1�C��2�C��3 �j �Ƃ����
���i ��0�C��1�C��2�C��3 �j �Ƃ����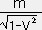 , �@��1��
, �@��1��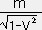 �u�� , �@��2��
�u�� , �@��2��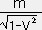 �u�� , �@��3��
�u�� , �@��3��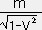 �u��
�u��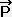 �̌n
�̌n �ɉ����鐬���́i���C�O�C�O�C�O�j�ł���B
�ɉ����鐬���́i���C�O�C�O�C�O�j�ł���B ��藝�œW�J����� �P�{�u2�^�Q�{�R�u4�^�i�Sx�Q�I�j�{�E�E�E�@�@�Ȃ̂łu�����������G�l���M�[��
��藝�œW�J����� �P�{�u2�^�Q�{�R�u4�^�i�Sx�Q�I�j�{�E�E�E�@�@�Ȃ̂łu�����������G�l���M�[���@�@�@�@�@�d�����{���u2�^�Q
�y ��0 �i���d�j�̓G�l���M�[�ł��� �z
�d�����Ŕ�������Ɓ@�@
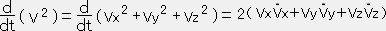 �ł��邩��
�ł��邩��
�@�@�@d�d�^d�� �� ���i �j�i�P�|�u2�j-3/2
�j�i�P�|�u2�j-3/2
�@�@�@�@�@�i�@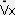 �����u���^�����C�@
�����u���^�����C�@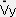 �����u���^�����C�@�@
�����u���^�����C�@�@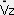 �����u���^�����C�@�@
�u�Q=�u���Q+�u���Q+�u���Q�@�j
�����u���^�����C�@�@
�u�Q=�u���Q+�u���Q+�u���Q�@�j
�j ��  �@�C�@�@�@�k �� �i�P�|�u2�j �Ƃ�����
�@�C�@�@�@�k �� �i�P�|�u2�j �Ƃ�����
�@�@�@d�d �� ���j�k-3/2 d�� �� ���i�i �j�i�P�|�u2�j�{�j�u2 �j �k-3/2 �j d��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �i �j�k-1/2 �{�j�u2 �k-3/2 �j d��
�j�k-1/2 �{�j�u2 �k-3/2�@�ɉ����č��� �j �� �u2 ��W�J�����
�@�@�@�j�k-1/2 �{�j�u2 �k-3/2�@���@�i �j �k-1/2 �{ �i�u���Q+�u���Q+�u���Q�j �j �k-3/2
�j �k-1/2 �{ �i�u���Q+�u���Q+�u���Q�j �j �k-3/2
�w�C�@�x�C�@�y�̍��ɂ��ꂼ��܂Ƃ߂��
�@�@�@�j�k-1/2 �{�j�u2 �k-3/2�@���@�iVx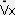 �k-1/2 �{Vx2 �j �k-3/2�j
�k-1/2 �{Vx2 �j �k-3/2�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�iVy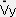 �k-1/2 �{Vy2 �j �k-3/2�j
�k-1/2 �{Vy2 �j �k-3/2�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�iVz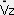 �k-1/2 �{Vz2 �j �k-3/2�j
�k-1/2 �{Vz2 �j �k-3/2�j
�������u������ , �������u������ , �������u������ ��p�����
�@�@�@�i�j�k-1/2 �{�j�u2 �k-3/2�j �����@���@�i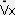 �k-1/2 �{Vx �j �k-3/2�j ����
�k-1/2 �{Vx �j �k-3/2�j ����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{ �i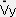 �k-1/2 �{Vy �j �k-3/2�j ����
�k-1/2 �{Vy �j �k-3/2�j ����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{ �i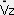 �k-1/2 �{Vz �j �k-3/2�j ����
�k-1/2 �{Vz �j �k-3/2�j ����
�]����
�@�@�@d�d �� ���i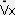 �k-1/2 �{Vx �j �k-3/2�j ����
�k-1/2 �{Vx �j �k-3/2�j ����
�@�@�@�@�@�@�@�{���i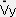 �k-1/2 �{Vy �j �k-3/2�j ����
�k-1/2 �{Vy �j �k-3/2�j ����
�@�@�@�@�@�@�@�{���i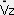 �k-1/2 �{Vz �j �k-3/2�j �����@�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�@
�k-1/2 �{Vz �j �k-3/2�j �����@�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�@
�͂��^�����̎��Ԃɑ���ω����Œ�`����邩��X�����̗͂�fx�Ƃ����
���l��Y�����̗͂� fy �Ƃ����
���l��Z�����̗͂� fz �Ƃ����
�@,�@�A,�@�B,�@�C�@���
d�d �� ��fx�����{��fy�����{��fz����
���ӂ�ϕ������ �d �� ��fx�w�{��fy�x�{��fz�y �{�b �@�@�u���O �̎� �d���� �Ȃ̂� �b����
�@�@�@�@�@�� �d �� ���{��fx�w�{��fy�x�{��fz�y
��L�̎��̉E�ӂ̑�P�������͐Î~�G�l���M�[�� ��fx�w�{��fy�x�{��fz�y �͉^���G�l���M�[�ł���B
| d�d�^d�� �� �� |  |
�^�Q |
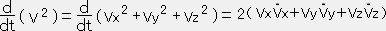 �ł��邩��
�ł��邩���@�@�@d�d�^d�� �� ���i
 �j�i�P�|�u2�j-3/2
�j�i�P�|�u2�j-3/2 �@�@�@�@�@�i�@
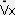 �����u���^�����C�@
�����u���^�����C�@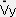 �����u���^�����C�@�@
�����u���^�����C�@�@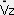 �����u���^�����C�@�@
�u�Q=�u���Q+�u���Q+�u���Q�@�j
�����u���^�����C�@�@
�u�Q=�u���Q+�u���Q+�u���Q�@�j �@�C�@�@�@�k �� �i�P�|�u2�j �Ƃ�����
�@�C�@�@�@�k �� �i�P�|�u2�j �Ƃ������@�@�@d�d �� ���j�k-3/2 d�� �� ���i�i �j�i�P�|�u2�j�{�j�u2 �j �k-3/2 �j d��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� �� �i �j�k-1/2 �{�j�u2 �k-3/2 �j d��
�@�@�@�j�k-1/2 �{�j�u2 �k-3/2�@���@�i
 �j �k-1/2 �{ �i�u���Q+�u���Q+�u���Q�j �j �k-3/2
�j �k-1/2 �{ �i�u���Q+�u���Q+�u���Q�j �j �k-3/2�@�@�@�j�k-1/2 �{�j�u2 �k-3/2�@���@�iVx
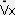 �k-1/2 �{Vx2 �j �k-3/2�j
�k-1/2 �{Vx2 �j �k-3/2�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�iVy
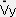 �k-1/2 �{Vy2 �j �k-3/2�j
�k-1/2 �{Vy2 �j �k-3/2�j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�iVz
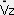 �k-1/2 �{Vz2 �j �k-3/2�j
�k-1/2 �{Vz2 �j �k-3/2�j�@�@�@�i�j�k-1/2 �{�j�u2 �k-3/2�j �����@���@�i
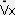 �k-1/2 �{Vx �j �k-3/2�j ����
�k-1/2 �{Vx �j �k-3/2�j �����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{ �i
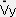 �k-1/2 �{Vy �j �k-3/2�j ����
�k-1/2 �{Vy �j �k-3/2�j �����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{ �i
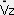 �k-1/2 �{Vz �j �k-3/2�j ����
�k-1/2 �{Vz �j �k-3/2�j �����@�@�@d�d �� ���i
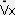 �k-1/2 �{Vx �j �k-3/2�j ����
�k-1/2 �{Vx �j �k-3/2�j �����@�@�@�@�@�@�@�{���i
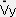 �k-1/2 �{Vy �j �k-3/2�j ����
�k-1/2 �{Vy �j �k-3/2�j �����@�@�@�@�@�@�@�{���i
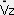 �k-1/2 �{Vz �j �k-3/2�j �����@�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�@
�k-1/2 �{Vz �j �k-3/2�j �����@�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�@| �@�@�@fx�� |  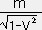 �ux �ux |
�� ���i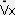 �k-1/2 �{Vx �j �k-3/2�j�E�E�E�E�E�A �k-1/2 �{Vx �j �k-3/2�j�E�E�E�E�E�A |
| �@�@�@fy�� |  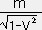 �uy �uy |
�� ���i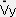 �k-1/2 �{Vy �j �k-3/2�j�E�E�E�E�E�B �k-1/2 �{Vy �j �k-3/2�j�E�E�E�E�E�B |
| �@�@�@fz�� |  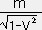 �uz �uz |
�� ���i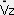 �k-1/2 �{Vz �j �k-3/2�j�E�E�E�E�E�E�C �k-1/2 �{Vz �j �k-3/2�j�E�E�E�E�E�E�C |
���ӂ�ϕ������ �d �� ��fx�w�{��fy�x�{��fz�y �{�b �@�@�u���O �̎� �d���� �Ȃ̂� �b����
��L�̎��̉E�ӂ̑�P�������͐Î~�G�l���M�[�� ��fx�w�{��fy�x�{��fz�y �͉^���G�l���M�[�ł���B
�T�D�X�J���[��
(1) �x�N�g���̑傫��
 �̑傫����
�̑傫�����@�@�@���@
 2��
2�� �E
�E ���[�i
���[�i �j2�{�i
�j2�{�i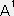 �j2
�{�i
�j2
�{�i �j2�{�i
�j2�{�i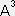 �j2
�j2
�ƒ�`�o����B���̑傫���͕��ɂ��Ȃ�B
 2 �����̎��͋�ԓI�x�N�g���ŁA�[���Ȃ�k���x�N�g���A���Ȃ玞�ԓI�x�N�g���Ƃ����B�k���x�N�g���̓[���x�N�g���ł͂Ȃ��B�[���x�N�g���͑S�Ă̐������[���ł��邪�A�k���x�N�g����
2 �����̎��͋�ԓI�x�N�g���ŁA�[���Ȃ�k���x�N�g���A���Ȃ玞�ԓI�x�N�g���Ƃ����B�k���x�N�g���̓[���x�N�g���ł͂Ȃ��B�[���x�N�g���͑S�Ă̐������[���ł��邪�A�k���x�N�g���� 2 �� �O �ł͂��邪�K�������S�Ă̐������[���Ƃ����킯�ł͂Ȃ��B
2 �� �O �ł͂��邪�K�������S�Ă̐������[���Ƃ����킯�ł͂Ȃ��B
(2) ��̃x�N�g���̃X�J���[�ρi���ρj
 �{
�{ �j�E�i
�j�E�i �{
�{ �j��
�i
�j��
�i �j2�{�i
�j2�{�i �j2�{�Q
�j2�{�Q �E
�E
�@�@�@�i
 �{
�{ �j�E�i
�j�E�i �{
�{ �j��
-(A0+B0)2+(A1+B1)2
+(A2+B2)2+(A3+B3)2
�j��
-(A0+B0)2+(A1+B1)2
+(A2+B2)2+(A3+B3)2�@�@�@�@�@�@�@��-(A0)2+(A1)2 +(A2)2+(A3)2 -(B0)2+(B1)2 +(B2)2+(B3)2
�@�@�@�@�@�@�@�@+2(-A0B0+A1B1+A2B2+A3B3)
 �E
�E ��
���@�@�@���@
 �E
�E ��-A0B0+A1B1+A2B2+A3B3 �ƂȂ�B
��-A0B0+A1B1+A2B2+A3B3 �ƂȂ�B �E
�E �� 0 �Ȃ��̃x�N�g��
�� 0 �Ȃ��̃x�N�g�� ��
�� �͒������Ă���Ƃ����B
�͒������Ă���Ƃ����B���̃X�J���[�ς͑S�Ă̌n�œ������l���Ƃ�i�ؖ��͉��L�Q�Ɓj�B
�y �X�J���[�ς͑S�Ă̌n�œ������l���Ƃ� �z
 �{
�{ �j�E�i
�j�E�i �{
�{ �j��
�j�� 2�{
2�{ 2�{�Q
2�{�Q �E
�E �@�ł���B
�@�ł���B
 �j2�{�i
�j2�{�i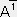 �j2�{�i
�j2�{�i �j2�{�i
�j2�{�i �j2
�j2�ł��邩��
 2�A
2�A 2�y�сi
2�y�сi �{
�{ �j2
�͕s�ςł���B
�j2
�͕s�ςł���B�]����
 �E
�E ���s�ςł���B
���s�ςł���B�U�D�o�x�N�g���A�o��ԁi��������������j
(1) ��`���̒�`
�������͕��f���̑S�̂��q�Ƃ���B�q��̂S�����x�N�g��������u�Ƃ���B�u�̂��̂��̂̃x�N�g���ɂq�̐���Ή�������i�ʑ�����j����  �Ƃ���B�C�ӂ̃x�N�g��
�Ƃ���B�C�ӂ̃x�N�g��  �A
�A  �Ǝ����ɂɑ���
�Ǝ����ɂɑ���
�������A ���x�N�g������u��̈�`�����͑o�x�N�g�����͋��σx�N�g�����̓R�x�N�g���ƌĂԁB�u��̈�`���̏W�����u���ŕ\���A�x�N�g������u�����u�̑o��ԂƌĂԁB
���x�N�g������u��̈�`�����͑o�x�N�g�����͋��σx�N�g�����̓R�x�N�g���ƌĂԁB�u��̈�`���̏W�����u���ŕ\���A�x�N�g������u�����u�̑o��ԂƌĂԁB
(�L���̏�Ɂ`���������͈̂�`���i���o�x�N�g��)�A�����������̂̓x�N�g���ł���j
�@�@�@ �i
�i �j��
�j��  �i
�i
 �j��
�j�� 
 �i
�i �j�@
�j�@
 ��
��  �i
�i �j �Ƃ� ���� �i
�j �Ƃ� ���� �i  ��
�� �̐��� �j
�̐��� �j
�@�@�@ �i
�i �j��
�j�� 
 �@�@�i�����O�`�R�j�@�@�@�@�@�E�E�E �E�E�i�P�j
�@�@�i�����O�`�R�j�@�@�@�@�@�E�E�E �E�E�i�P�j
�@
 �Ƃ���B�C�ӂ̃x�N�g��
�Ƃ���B�C�ӂ̃x�N�g��  �A
�A  �Ǝ����ɂɑ���
�Ǝ����ɂɑ���
�@�@�@���@ �i
�i �{
�{ �j��
�j�� �i
�i �j�{
�j�{ �i
�i �j�@�@�@
�j�@�@�@ �i��
�i�� �j����
�j���� �i
�i �j
�j
 �i
�i �{
�{ �j��
�j�� �i
�i �j�{
�j�{ �i
�i �j�@�@�@
�j�@�@�@ �i��
�i�� �j����
�j���� �i
�i �j
�j
 ���x�N�g������u��̈�`�����͑o�x�N�g�����͋��σx�N�g�����̓R�x�N�g���ƌĂԁB�u��̈�`���̏W�����u���ŕ\���A�x�N�g������u�����u�̑o��ԂƌĂԁB
���x�N�g������u��̈�`�����͑o�x�N�g�����͋��σx�N�g�����̓R�x�N�g���ƌĂԁB�u��̈�`���̏W�����u���ŕ\���A�x�N�g������u�����u�̑o��ԂƌĂԁB(�L���̏�Ɂ`���������͈̂�`���i���o�x�N�g��)�A�����������̂̓x�N�g���ł���j
 �i
�i �j��
�j��  �i
�i
 �j��
�j�� 
 �i
�i �j�@
�j�@
 ��
��  �i
�i �j �Ƃ� ���� �i
�j �Ƃ� ���� �i  ��
�� �̐��� �j
�̐��� �j�@�@�@
 �i
�i �j��
�j�� 
 �@�@�i�����O�`�R�j�@�@�@�@�@�E�E�E �E�E�i�P�j
�@�@�i�����O�`�R�j�@�@�@�@�@�E�E�E �E�E�i�P�j�@
(2) �o��Ԃ̋���
�u�̈�̃x�N�g�� �ɑ��Ău*�ɉ������`��
�ɑ��Ău*�ɉ������`��  * �����̗l�ɒ�߂鎖���o����B�����e
* �����̗l�ɒ�߂鎖���o����B�����e  �ɑΉ�����q�̒l��
�ɑΉ�����q�̒l��
�@�@�@ *�i
*�i �j��
�j�� �i
�i �j�@�@�@�@�@�E�E�E�E�E�i�Q�j
�j�@�@�@�@�@�E�E�E�E�E�i�Q�j
 * ����`���ł��鎖���m�F����B
* ����`���ł��鎖���m�F����B
�i�Q�j�̎��� ��
��  �{
�{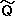 �Œu���������
�Œu���������  *�i
*�i �{
�{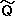 �j��(
�j��( �{
�{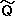 )�i
)�i �j��
�j�� �i
�i �j�{
�j�{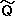 �i
�i �j
�j
�i�Q�j�̎��� �� ��
�� �� �Œu���������
�Œu���������  *�i��
*�i�� �j����
�j���� �i
�i �j
�j
�]����
�@�@�@ *�i
*�i �{
�{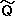 �j��
�j�� *�i
*�i �j�{
�j�{ *�i
*�i �j�@�C�@
�j�@�C�@ *�i��
*�i�� �j����
�j���� *�i
*�i �j�@�@�@�E�E�E�E�E�i�R�j
�j�@�@�@�E�E�E�E�E�i�R�j
����Ĉ�`���̒�`���  * ����`���ł��鎖���킩��B
* ����`���ł��鎖���킩��B
�u���u*�ɑo�ȋ�Ԃu**�������������ł��邩�� �ɑ��Č��܂�
�u*�̈�`��
�ɑ��Č��܂�
�u*�̈�`�� *��
*�� �Ɠ����ƌ��Ȃ������o����B
�Ɠ����ƌ��Ȃ������o����B
�]���Ău�̑o�ȋ�Ԃu*�̑o�ȋ�Ԃu**�͂u�ƂȂ�B ���ꂪ�u�Ƃu*�̋����ł���B
�i�Q�j�Ɓi�R�j�ɉ����� *��
*�� �Œu���������
�Œu���������
�@�@�@ �i
�i �j��
�j�� �i
�i �j�@�@�@�E�E�E�E�E�i�S�j
�j�@�@�@�E�E�E�E�E�i�S�j
�@�@�@ �i
�i �{
�{ �j��
�j�� �i
�i �j�{
�j�{ �i
�i �j�@�C�@
�j�@�C�@
 �i��
�i�� �j����
�j���� �i
�i �j�@�@�@�E�E�E�E�E�i�T�j
�j�@�@�@�E�E�E�E�E�i�T�j
�����藧�B
 �ɑ��Ău*�ɉ������`��
�ɑ��Ău*�ɉ������`��  * �����̗l�ɒ�߂鎖���o����B�����e
* �����̗l�ɒ�߂鎖���o����B�����e  �ɑΉ�����q�̒l��
�ɑΉ�����q�̒l���@�@�@
 *�i
*�i �j��
�j�� �i
�i �j�@�@�@�@�@�E�E�E�E�E�i�Q�j
�j�@�@�@�@�@�E�E�E�E�E�i�Q�j * ����`���ł��鎖���m�F����B
* ����`���ł��鎖���m�F����B�i�Q�j�̎���
 ��
��  �{
�{ �Œu���������
�Œu���������  *�i
*�i �{
�{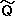 �j��(
�j��( �{
�{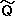 )�i
)�i �j��
�j�� �i
�i �j�{
�j�{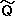 �i
�i �j
�j�i�Q�j�̎���
 �� ��
�� �� �Œu���������
�Œu���������  *�i��
*�i�� �j����
�j���� �i
�i �j
�j�]����
�@�@�@
 *�i
*�i �{
�{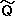 �j��
�j�� *�i
*�i �j�{
�j�{ *�i
*�i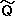 �j�@�C�@
�j�@�C�@ *�i��
*�i�� �j����
�j���� *�i
*�i �j�@�@�@�E�E�E�E�E�i�R�j
�j�@�@�@�E�E�E�E�E�i�R�j * ����`���ł��鎖���킩��B
* ����`���ł��鎖���킩��B�u���u*�ɑo�ȋ�Ԃu**�������������ł��邩��
 �ɑ��Č��܂�
�u*�̈�`��
�ɑ��Č��܂�
�u*�̈�`�� *��
*�� �Ɠ����ƌ��Ȃ������o����B
�Ɠ����ƌ��Ȃ������o����B�]���Ău�̑o�ȋ�Ԃu*�̑o�ȋ�Ԃu**�͂u�ƂȂ�B ���ꂪ�u�Ƃu*�̋����ł���B
�i�Q�j�Ɓi�R�j�ɉ�����
 *��
*�� �Œu���������
�Œu���������
 �i
�i �j��
�j�� �i
�i �j�@�@�@�E�E�E�E�E�i�S�j
�j�@�@�@�E�E�E�E�E�i�S�j�@�@�@
 �i
�i �{
�{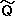 �j��
�j�� �i
�i �j�{
�j�{ �i
�i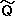 �j�@�C�@
�j�@�C�@
 �i��
�i�� �j����
�j���� �i
�i �j�@�@�@�E�E�E�E�E�i�T�j
�j�@�@�@�E�E�E�E�E�i�T�j
(3) ��`���̐���
�x�N�g���Ɠ����l�Ɉ�`�������������B�����͎��̂悤�ɒ�`�����B
�n�r�ł̈�`���̐��� �͌n�r�ł̊��x�N�g���o
�͌n�r�ł̊��x�N�g���o  �p��ϐ��ɂƂ������̒l�ł���B����
�p��ϐ��ɂƂ������̒l�ł���B����
�@�@�@���@ ��
�� �i
�i �j
�j
�n�r�ł̈�`���̐���
 �͌n�r�ł̊��x�N�g���o
�͌n�r�ł̊��x�N�g���o  �p��ϐ��ɂƂ������̒l�ł���B����
�p��ϐ��ɂƂ������̒l�ł���B���� ��
�� �i
�i �j
�j(4) ��`���̊��
�S�Ă̈�`���̏W���̓x�N�g���̋�Ԃ���邩��A��`����C�ӂȎl�̐��`�Ɨ��Ȋ��i���o�Ί��j��p���ĕ\�������o����B
�C�ӂ̃x�N�g��  ��
��  �̑惿����
�̑惿���� 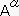 �ɑΉ�������i���ʑ�����j����
�ɑΉ�������i���ʑ�����j����  �Ƃ���B
�Ƃ���B  �͈ꎟ�`���ł���B�i�Y�����͏�t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB�j
�͈ꎟ�`���ł���B�i�Y�����͏�t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB�j
�@�@�@
 �͔C�ӂ̃x�N�g���Ȃ̂�
�͔C�ӂ̃x�N�g���Ȃ̂� 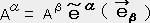 ���P���I�ɐ��藧�ׂɂ�
�@�@�@
���P���I�ɐ��藧�ׂɂ�
�@�@�@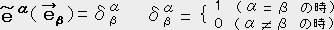
��̎��̓��Ԗڂ̈�`���i���o�x�N�g���j�̃��Ԗڂ̐�����^���Ă��鎖��������B�����̐������������낷��
�@�@�@ ���i�P�C�O�C�O�C�O�j�@�@
���i�P�C�O�C�O�C�O�j�@�@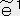 ���i�O�C�P�C�O�C�O�j�@�@
���i�O�C�P�C�O�C�O�j�@�@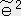 ���i0�C�O�C1�C�O�j�@�@
���i0�C�O�C1�C�O�j�@�@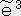 ���i�O�C�O�C�O�C�P�j
���i�O�C�O�C�O�C�P�j
 �A
�A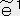 �A
�A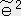 �A
�A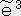 �͖��炩�ɐ��`�Ɨ��ł��邩��u���̊��i��`���̊��j�ƂȂ�B
����
�͖��炩�ɐ��`�Ɨ��ł��邩��u���̊��i��`���̊��j�ƂȂ�B
����  ��
��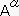
 �̗l�Ƀx�N�g��
�̗l�Ƀx�N�g��  �����x�N�g��
�����x�N�g�� �̐��`�����ŕ\�����l��
�̐��`�����ŕ\�����l��
��`��  ����`���̊��
����`���̊��  �̐��`�����ŕ\���鎖�������B�܂�
�̐��`�����ŕ\���鎖�������B�܂�
 �i
�i �j��
�j�� �Ƃ�������
�Ƃ�������  ��
��
 �ł��鎖�������B
�ł��鎖�������B
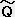 ��
��
 �Ƃ����ƁA
�Ƃ����ƁA
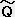 �i
�i �j��
�j��
 �i
�i �j��
�j�� ��
�� �i
�i �j
�j
 ��
��
 �Ƃ���ƁA
�Ƃ���ƁA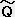 �i
�i �j��
�j��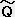 �i
�i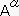
 �j��
�j��
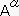
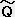 �i
�i �j
�j
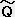 �i
�i �j��
�j�� �i
�i �j ������
�j ������
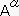
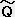 �i
�i �j��
�j��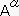
 �i
�i �j ��
�j ��
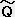 �i
�i �j��
�j�� �i
�i �j
�j
 �͔C�ӂȃx�N�g��������
�͔C�ӂȃx�N�g��������
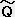 ��
��
�@�@�@���@ ��
��

 ��
��  �̑惿����
�̑惿���� 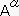 �ɑΉ�������i���ʑ�����j����
�ɑΉ�������i���ʑ�����j����  �Ƃ���B
�Ƃ���B  �͈ꎟ�`���ł���B�i�Y�����͏�t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB�j
�͈ꎟ�`���ł���B�i�Y�����͏�t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB�j
 �͔C�ӂ̃x�N�g���Ȃ̂�
�͔C�ӂ̃x�N�g���Ȃ̂� 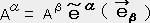 ���P���I�ɐ��藧�ׂɂ�
���P���I�ɐ��藧�ׂɂ�
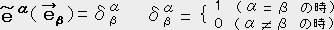
 ���i�P�C�O�C�O�C�O�j�@�@
���i�P�C�O�C�O�C�O�j�@�@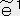 ���i�O�C�P�C�O�C�O�j�@�@
���i�O�C�P�C�O�C�O�j�@�@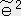 ���i0�C�O�C1�C�O�j�@�@
���i0�C�O�C1�C�O�j�@�@ ���i�O�C�O�C�O�C�P�j
���i�O�C�O�C�O�C�P�j �A
�A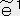 �A
�A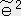 �A
�A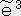 �͖��炩�ɐ��`�Ɨ��ł��邩��u���̊��i��`���̊��j�ƂȂ�B
�͖��炩�ɐ��`�Ɨ��ł��邩��u���̊��i��`���̊��j�ƂȂ�B
 ��
��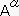
 �̗l�Ƀx�N�g��
�̗l�Ƀx�N�g��  �����x�N�g��
�����x�N�g�� �̐��`�����ŕ\�����l��
�̐��`�����ŕ\�����l�� ����`���̊��
����`���̊��  �̐��`�����ŕ\���鎖�������B�܂�
�̐��`�����ŕ\���鎖�������B�܂� �i
�i �j��
�j�� �Ƃ�������
�Ƃ�������  ��
��
 �ł��鎖�������B
�ł��鎖�������B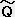 ��
��
 �Ƃ����ƁA
�Ƃ����ƁA
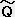 �i
�i �j��
�j��
 �i
�i �j��
�j�� ��
�� �i
�i �j
�j  ��
��
 �Ƃ���ƁA
�Ƃ���ƁA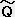 �i
�i �j��
�j��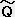 �i
�i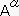
 �j��
�j��
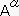
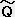 �i
�i �j
�j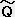 �i
�i �j��
�j�� �i
�i �j ������
�j ������
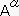
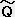 �i
�i �j��
�j��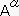
 �i
�i �j ��
�j ��
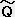 �i
�i �j��
�j�� �i
�i �j
�j  �͔C�ӂȃx�N�g��������
�͔C�ӂȃx�N�g��������
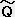 ��
��
 ��
��

(5) ��`���̐����̕ϊ�
�Y�����͉��t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB
�n�r����n �ւ̕ϊ���
�ւ̕ϊ���
�@�@�@���@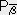 ��
��  �i
�i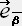 �j��
�j��  �i
�i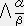
 �j��
�j�� 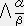
 �n
�n ����n�r�ւ̕ϊ���
����n�r�ւ̕ϊ���
�@�@�@���@ ��
��  �i
�i �i
�i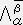
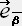 �j��
�j�� 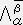
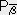
 �ւ̕ϊ���
�ւ̕ϊ���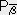 ��
��  �i
�i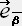 �j��
�j��  �i
�i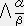
 �j��
�j�� 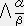

 ����n�r�ւ̕ϊ���
����n�r�ւ̕ϊ��� ��
��  �i
�i �i
�i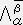
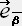 �j��
�j�� 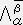
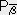
(6) ��`���̊��̕ϊ�
�Y�����͏�t���Ƃ���B�ڍׂ�8. ���ρA���σx�N�g���ƓY�����̈ʒu���Q�ƁB
�n ����n�r�ւ̕ϊ���
����n�r�ւ̕ϊ���
�@�@�@
 ��
��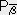
 ��
��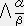


�@�@�@ �͔C�ӂ�����
�͔C�ӂ�����
�@�@�@�@�@�@���@ ��
��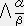
 ���l�ɁA�n�r����n
���l�ɁA�n�r����n �ւ̕ϊ���
�ւ̕ϊ���
�@�@�@�@�@�@���@ ��
��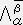

 ����n�r�ւ̕ϊ���
����n�r�ւ̕ϊ���
 ��
��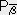
 ��
��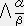


�@�@�@
 �͔C�ӂ�����
�͔C�ӂ������@�@�@�@�@�@���@
 ��
��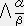

 �ւ̕ϊ���
�ւ̕ϊ����@�@�@�@�@�@���@
 ��
��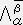

(7) ��`���̑傫���ƃX�J���[��
�x�N�g���̏ꍇ�Ɠ����悤�Ɉ�`���̑傫����
�@�@�@���@ 2��
2�� �E
�E ���[�i�o0�j2�{�i�o1�j2
�{�i�o2�j2�{�i�o3�j2
���[�i�o0�j2�{�i�o1�j2
�{�i�o2�j2�{�i�o3�j2
�X�J���[�ς�
�@�@�@���@ �E
�E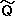 ���[�o0�p0�{�o1�p1�{�o2�p2�{�o3�p3
���[�o0�p0�{�o1�p1�{�o2�p2�{�o3�p3
�@�@�@���@
 2��
2�� �E
�E ���[�i�o0�j2�{�i�o1�j2
�{�i�o2�j2�{�i�o3�j2
���[�i�o0�j2�{�i�o1�j2
�{�i�o2�j2�{�i�o3�j2
�@�@�@���@
 �E
�E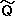 ���[�o0�p0�{�o1�p1�{�o2�p2�{�o3�p3
���[�o0�p0�{�o1�p1�{�o2�p2�{�o3�p3
�V�D��`���A�o��Ԃ̗�
�x�N�g���ƈ�`���͂��݂��ɑo�ΓI�Ȃ��̂ł���B���̂悤�ȑo��Ԃ͕������w�̑��̕���ɂ������邱�Ƃ��o����d�v�ȊT�O�ł���B
(1) �s�x�N�g���͈�`��
�s�x�N�g�����iP0,P1,P2,P3�j

�@�@�@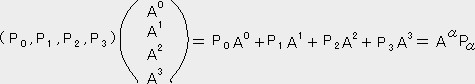
�㎮�́@6. �o�x�N�g���A�o����ɉ����鎮�i�P�j�Ɠ����ł���B�]���čs�x�N�g���͗�x�N�g����̈�`���ł���B

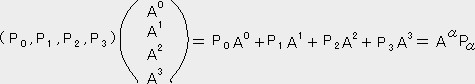
�㎮�́@6. �o�x�N�g���A�o����ɉ����鎮�i�P�j�Ɠ����ł���B�]���čs�x�N�g���͗�x�N�g����̈�`���ł���B
(2) ���̔����͈�`��
�~���R�t�X�L�[�̎l��������̂���̈�̊e�_�i��,��,��,���j�ɐ����i��,��,��,���j���Ή��������鎞�A���̓X�J���[��ł���Ƃ����B���闱�q�i���͕��́j�̐��E���͂���ɉ����Ă̌ŗL���ԃт̊��ł���B�����e�_�i��,��,��,���j�̓т̊��ł���B�]���ăX�J���[�ꃳ���т̊��ƂȂ�B
�������̔����@�ɂ�莟�̎������藧�B
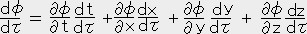
��̎��ɉ�����  ,
, 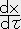 ,
, 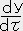 ,
, 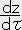 ���l�����x�ŗ��q�̐��E���ɐڂ���x�N�g��
���l�����x�ŗ��q�̐��E���ɐڂ���x�N�g�� �̐����ł���B
�̐����ł���B
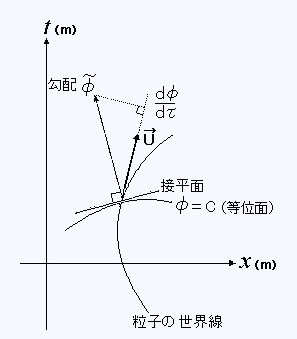 ��̎��ɉ����ăx�N�g��
��̎��ɉ����ăx�N�g��  ���琔d�Ӂ^d���������@�����������͖��炩�ł���B���̐��̓x�N�g��
���琔d�Ӂ^d���������@�����������͖��炩�ł���B���̐��̓x�N�g��  �̕����̃��̔����W���Ƃ����A
�̕����̃��̔����W���Ƃ����A ���ڃx�N�g���ƂȂ�Ȑ���ł̃��̕ω�����\���B�܂����̐�d�Ӂ^d���͖��炩��
���ڃx�N�g���ƂȂ�Ȑ���ł̃��̕ω�����\���B�܂����̐�d�Ӂ^d���͖��炩�� �̐��`���ł���A�]���Ĉ�`�����`�������ƂɂȂ�B
�̐��`���ł���A�]���Ĉ�`�����`�������ƂɂȂ�B
�U. �o�x�N�g���A�o����ɉ����鎮�i�P�j�Ɣ�ׂ邱�Ƃɂ�肱�̈�`���͐���
�@�@�@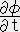 ,
,  ,
, 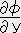 ,
, 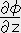
�����B���̈�`�������̌��z�ƌĂсA �i ����
�i ���� �j �Ə����B
�j �Ə����B
�����b�i�萔�j�ƂȂ铙�ʖʏ�̓_�it(��),x(��),y(��),z(��)�j�ɉ�����ڕ��ʂ̕�������

�]���āA���z  �i ����
�i ���� �j �͐ڕ��ʂɐ����ł��邱�Ƃ�������B����𐂒���`���Ƃ����B
�j �͐ڕ��ʂɐ����ł��邱�Ƃ�������B����𐂒���`���Ƃ����B
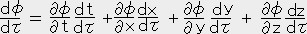
 ,
, 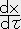 ,
, 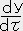 ,
, 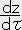 ���l�����x�ŗ��q�̐��E���ɐڂ���x�N�g��
���l�����x�ŗ��q�̐��E���ɐڂ���x�N�g�� �̐����ł���B
�̐����ł���B
 ���琔d�Ӂ^d���������@�����������͖��炩�ł���B���̐��̓x�N�g��
���琔d�Ӂ^d���������@�����������͖��炩�ł���B���̐��̓x�N�g��  �̕����̃��̔����W���Ƃ����A
�̕����̃��̔����W���Ƃ����A ���ڃx�N�g���ƂȂ�Ȑ���ł̃��̕ω�����\���B�܂����̐�d�Ӂ^d���͖��炩��
���ڃx�N�g���ƂȂ�Ȑ���ł̃��̕ω�����\���B�܂����̐�d�Ӂ^d���͖��炩�� �̐��`���ł���A�]���Ĉ�`�����`�������ƂɂȂ�B
�̐��`���ł���A�]���Ĉ�`�����`�������ƂɂȂ�B�U. �o�x�N�g���A�o����ɉ����鎮�i�P�j�Ɣ�ׂ邱�Ƃɂ�肱�̈�`���͐���
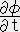 ,
,  ,
, 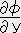 ,
, 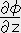
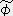 �i ����
�i ���� �j �Ə����B
�j �Ə����B�����b�i�萔�j�ƂȂ铙�ʖʏ�̓_�it(��),x(��),y(��),z(��)�j�ɉ�����ڕ��ʂ̕�������

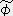 �i ����
�i ���� �j �͐ڕ��ʂɐ����ł��邱�Ƃ�������B����𐂒���`���Ƃ����B
�j �͐ڕ��ʂɐ����ł��邱�Ƃ�������B����𐂒���`���Ƃ����B
�W�D���ρA���σx�N�g���ƓY�����̈ʒu
���x�N�g���Ɠ����ϊ����i�������ϊ��s���p����j������(covariant)�x�N�g���ƌĂ��R���ł���B���ʂ̃x�N�g���͊��x�N�g���Ƃ͋t�ɕϊ�����i���t�̕ϊ��s���p����j�̂ŁA���σx�N�g���ƌĂ��B�ŋ߂ł͔��σx�N�g����P�Ƀx�N�g���A���σx�N�g������`�����͑o�x�N�g���ƌĂԂ̂����ʂł���B
���@���x�N�g���Ɠ����ϊ����̎��́A�Y�����͉��t���Ƃ��A�t�̕ϊ����̎��͓Y�����͏�t���ƒ�߂�B
���@���[�����c�ϊ��s�� 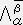 ��
��
���@���[�����c�ϊ��s��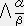 ��
��
�@�@
�E�x�N�g���i�����σx�N�g���j�̐����͋t�̕ϊ���������A�Y�����͏�t���ł���B
�E��`���̊��̕ϊ����t�̕ϊ���������A�Y�����͏�t���ł���B
�E��`���i���o�x�N�g���A���σx�N�g���j�̐����͓����ϊ���������A�Y�����͉��t���ł���B
�E��`���̊��̕ϊ����t�̕ϊ���������A�Y�����͏�t���ł���B
�E��`���i���o�x�N�g���A���σx�N�g���j�̐����͓����ϊ���������A�Y�����͉��t���ł���B
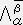 ��
��
�E�n ����n�r�ւ̊��x�N�g���̕ϊ��̎��g�p����B
����n�r�ւ̊��x�N�g���̕ϊ��̎��g�p����B
�E�n�r����n �ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
�E�n�r����n �ւ̈�`���̊��̕ϊ��̎��g�p����B
�ւ̈�`���̊��̕ϊ��̎��g�p����B
�E�n ����n�r�ւ̈�`���̐����̕ϊ��̎��g�p����B
����n�r�ւ̈�`���̐����̕ϊ��̎��g�p����B
 ����n�r�ւ̊��x�N�g���̕ϊ��̎��g�p����B
����n�r�ւ̊��x�N�g���̕ϊ��̎��g�p����B�E�n�r����n
 �ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B�E�n�r����n
 �ւ̈�`���̊��̕ϊ��̎��g�p����B
�ւ̈�`���̊��̕ϊ��̎��g�p����B�E�n
 ����n�r�ւ̈�`���̐����̕ϊ��̎��g�p����B
����n�r�ւ̈�`���̐����̕ϊ��̎��g�p����B���@���[�����c�ϊ��s��
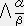 ��
��
�E�n�r����n �ւ̊��x�N�g���̕ϊ��̎��g�p����B
�ւ̊��x�N�g���̕ϊ��̎��g�p����B
�E�n ����n�r�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
����n�r�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
�E�n ����n�r�ւ̈�`���̊��̕ϊ��̎��g�p����B
����n�r�ւ̈�`���̊��̕ϊ��̎��g�p����B
�E�n�r����n �ւ̈�`���̐����̕ϊ��̎��g�p����B
�ւ̈�`���̐����̕ϊ��̎��g�p����B
 �ւ̊��x�N�g���̕ϊ��̎��g�p����B
�ւ̊��x�N�g���̕ϊ��̎��g�p����B�E�n
 ����n�r�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B
����n�r�ւ̃x�N�g���̐����̕ϊ��̎��g�p����B�E�n
 ����n�r�ւ̈�`���̊��̕ϊ��̎��g�p����B
����n�r�ւ̈�`���̊��̕ϊ��̎��g�p����B�E�n�r����n
 �ւ̈�`���̐����̕ϊ��̎��g�p����B
�ւ̈�`���̐����̕ϊ��̎��g�p����B
�@�@
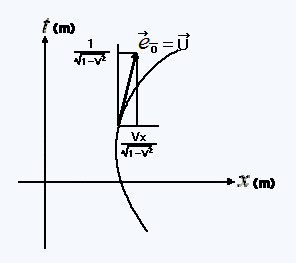
�@�@�@�@�@( ���� �@V=Vx )
�@V=Vx )

�@�@�@�@�@( ����
 �@V=Vx )
�@V=Vx )