特殊相対論入門
< 目次へ >
特殊相対性理論はアインシュタインにより1905年に発表され、これまで絶対的で、普遍的だと思われていた時間、空間、質量や長さといった概念を根本から覆すものでありました。
現在では既にその理論の正しさが種々の観測、実験により確認されています。
1.特殊相対論の基本原理
特殊相対論は二つの仮説から成り立っている。
(1) 光速不変の原理
地上に静止している観測者が同じく地上に静止している自動車のヘッドランプより出た光の速さを測った時その速さは3x108m/sで、自動車が時速100kmで走っていても地上に静止している観測者が光の速さを測った時その速さは3x108m/s(3x108m/s+100km/時にならない) である。これはマイケルソン・モーレーの実験により確認されている。では時速100kmで走っている自動車より時速150kmで投げたられたボールを地上に静止している観測者が測った時、時速250kmになるのは何故だろう。250kmという数字ははたしては正しいのであろうか?。この疑問は 8. 速度の合成則で解消される。
光速を超える仮想粒子タキオンが考えられているが現在のところ見つかっていない。
光速を超える仮想粒子タキオンが考えられているが現在のところ見つかっていない。
(2) 相対性原理
自然法則は全ての慣性系に対して同じである。例えばニュートンの運動の第一法則は地上でも等速直線運動をしている電車の中でも同じように成り立つ。
光速不変の原理により光の速さを無次元量で1と定義すると時間をmで表わす事ができる。
1=3x108m/s, 1s=3x108m, 1m=(3x108)-1sとなる。 時間の1秒とは3x108mの事である。時間の1mとは(3x108)-1sの事である。 以後光の速さを無次元量で1と定義した「自然単位系」を採用する。 3x107m/sで走っている粒子の速さは
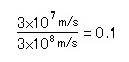 となる。
となる。
1=3x108m/s, 1s=3x108m, 1m=(3x108)-1sとなる。 時間の1秒とは3x108mの事である。時間の1mとは(3x108)-1sの事である。 以後光の速さを無次元量で1と定義した「自然単位系」を採用する。 3x107m/sで走っている粒子の速さは
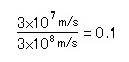 となる。
となる。
上記の定義(付録1及び付録2を参照)によりE=MC2を簡単に導く事が出来る。
1=3x1010cms-1  cm2s-2= 1/c2
(c=3x1010)
cm2s-2= 1/c2
(c=3x1010)
1エルグ=1gcm2s-2=1gx1/c2
従って 1g=c2エルグ mg なら mg=mc2エルグ
詳細は「9. 物質=エネルギー(E=MC2)と質量の増加を参照
 cm2s-2= 1/c2
(c=3x1010)
cm2s-2= 1/c2
(c=3x1010)1エルグ=1gcm2s-2=1gx1/c2
従って 1g=c2エルグ mg なら mg=mc2エルグ
2.ガリレイ変換とローレンツ変換
慣性系Sに於ける事象の時空座標を(t,x,y,z)、その事象の別の慣性系 に於ける時空座標を(
に於ける時空座標を( ,
, ,
, ,
, )
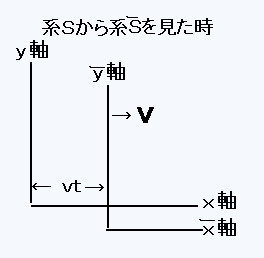
としてこの二つの座標の関係を古典物理学(ガリレイ変換)と相対性理論(ローレンツ変換)の立場から求めてみる。空間座標の関係を求める為以下のような約束をしておく。
)
としてこの二つの座標の関係を古典物理学(ガリレイ変換)と相対性理論(ローレンツ変換)の立場から求めてみる。空間座標の関係を求める為以下のような約束をしておく。

 に於ける時空座標を(
に於ける時空座標を( ,
, ,
, ,
, )
としてこの二つの座標の関係を古典物理学(ガリレイ変換)と相対性理論(ローレンツ変換)の立場から求めてみる。空間座標の関係を求める為以下のような約束をしておく。
)
としてこの二つの座標の関係を古典物理学(ガリレイ変換)と相対性理論(ローレンツ変換)の立場から求めてみる。空間座標の関係を求める為以下のような約束をしておく。
①三つの空間座標軸は互いに直交している
②二つの慣性系Sと の対応する座標軸は互いに平行である
の対応する座標軸は互いに平行である
③t= =0で二つの座標系の原点は一致している
=0で二つの座標系の原点は一致している
④ はSに対してX軸の正の方向に速度Vで動いている。Y=
はSに対してX軸の正の方向に速度Vで動いている。Y= 、Z=
、Z= である。
である。
②二つの慣性系Sと
 の対応する座標軸は互いに平行である
の対応する座標軸は互いに平行である③t=
 =0で二つの座標系の原点は一致している
=0で二つの座標系の原点は一致している④
 はSに対してX軸の正の方向に速度Vで動いている。Y=
はSに対してX軸の正の方向に速度Vで動いている。Y= 、Z=
、Z= である。
である。

(1)ガリレイ変換
 =XーVt , X=
=XーVt , X= +V
+V
この様な座標変換をガリレイ変換と言う。この変換はVが光速に比べて十分小さい時だけ成り立つ近似式である。ガリレイ変換(古典物理学)ではどのような慣性系においても時間は不変であるという絶対時間が仮定されているので t=
 である。
である。(2)ローレンツ変換
ローレンツ変換に於いては t≠ なので速度Vに依存する係数γを導入して座標変換式を求める。
なので速度Vに依存する係数γを導入して座標変換式を求める。
 =γ(X-Vt) , X=γ(
=γ(X-Vt) , X=γ( +V
+V )
・・・・・・・・・・・・・・・ (1)
)
・・・・・・・・・・・・・・・ (1)
光速不変の原理より、光は系Sと系 において同じ速度をもつから t=
において同じ速度をもつから t= =0 から出発した光は時間t(
=0 から出発した光は時間t( )後にX(
)後にX( )に達するので X=t ,
)に達するので X=t ,  =
= が成り立つ。
が成り立つ。
これを(1)へ代入して両式の積をとると t =γ2(1-V2)t
=γ2(1-V2)t となり
となり
従って γ= を得る。
を得る。
(1)の第1式の を第2式に代入して整理すると
を第2式に代入して整理すると
◆ =γ(t-VX) ,
=γ(t-VX) ,  =γ(X-Vt) ,
=γ(X-Vt) ,  =Y ,
=Y ,  =Z
・・・・・・・・・・・・・・・ (2)
=Z
・・・・・・・・・・・・・・・ (2)
これがX方向への速度Vのブーストと呼ばれる最も簡単な形である。系Sから系 への変換行列
への変換行列 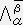 と系
と系 から系Sへの変換行列
から系Sへの変換行列  は下記のようになる。
は下記のようになる。

 なので速度Vに依存する係数γを導入して座標変換式を求める。
なので速度Vに依存する係数γを導入して座標変換式を求める。 =γ(X-Vt) , X=γ(
=γ(X-Vt) , X=γ( +V
+V )
・・・・・・・・・・・・・・・ (1)
)
・・・・・・・・・・・・・・・ (1)光速不変の原理より、光は系Sと系
 において同じ速度をもつから t=
において同じ速度をもつから t= =0 から出発した光は時間t(
=0 から出発した光は時間t( )後にX(
)後にX( )に達するので X=t ,
)に達するので X=t ,  =
= が成り立つ。
が成り立つ。これを(1)へ代入して両式の積をとると t
 =γ2(1-V2)t
=γ2(1-V2)t となり
となり従って γ=
 を得る。
を得る。(1)の第1式の
 を第2式に代入して整理すると
を第2式に代入して整理すると◆
 =γ(t-VX) ,
=γ(t-VX) ,  =γ(X-Vt) ,
=γ(X-Vt) ,  =Y ,
=Y ,  =Z
・・・・・・・・・・・・・・・ (2)
=Z
・・・・・・・・・・・・・・・ (2)これがX方向への速度Vのブーストと呼ばれる最も簡単な形である。系Sから系
 への変換行列
への変換行列  と系
と系 から系Sへの変換行列
から系Sへの変換行列  は下記のようになる。
は下記のようになる。

3.ミンコフスキーの時空図
特殊相対論を学ぶ上で時空図は非常に有効な方法である。時空図は縦軸に時間、横軸に空間座標をとった座標系の事である。下記にY=0, Z=0の面で四次元空間をスライスした図が示されている。光子、粒子、物体の運動はこの時空図(ミンコフスキーの空間)の中で直線又は曲線で表わされ、その直線又は曲線を世界線という。

 軸及び
軸及び 軸はどこだろうか?
軸はどこだろうか?
 軸はローレンツ変換式
軸はローレンツ変換式
 =γ(X-Vt)において
=γ(X-Vt)において
 =0とおいた式t=X/Vという直線が
=0とおいた式t=X/Vという直線が 軸となる。
軸となる。
 軸はローレンツ変換式
軸はローレンツ変換式
 =γ(t-VX)において
=γ(t-VX)において
 =0とおいた式 t=VXという直線が
=0とおいた式 t=VXという直線が 軸となる。
軸となる。
系Sに対しX軸の正の方向に速度Vで運動している粒子(系 )の時間軸
)の時間軸 と空間軸
と空間軸 を系Sから見た時空図に描いてみる。
を系Sから見た時空図に描いてみる。
V=dx/dt より Vt=X 光の場合 V=1 なので t=X となり45゜の傾きをもった直線となる。


 軸及び
軸及び 軸はどこだろうか?
軸はどこだろうか? 軸はローレンツ変換式
軸はローレンツ変換式
 =γ(X-Vt)において
=γ(X-Vt)において
 =0とおいた式t=X/Vという直線が
=0とおいた式t=X/Vという直線が 軸となる。
軸となる。 軸はローレンツ変換式
軸はローレンツ変換式
 =γ(t-VX)において
=γ(t-VX)において
 =0とおいた式 t=VXという直線が
=0とおいた式 t=VXという直線が 軸となる。
軸となる。系Sに対しX軸の正の方向に速度Vで運動している粒子(系
 )の時間軸
)の時間軸 と空間軸
と空間軸 を系Sから見た時空図に描いてみる。
を系Sから見た時空図に描いてみる。V=dx/dt より Vt=X 光の場合 V=1 なので t=X となり45゜の傾きをもった直線となる。

4.間 隔 の 不 変 性
前節で座標軸は分かった。その軸に対し間隔の不変性を用いて目盛り付けを行う。その前に間隔の不変性の証明を行う。間隔とは ー(⊿t)2+(⊿X)2+(⊿Y)2+(⊿Z)2の事である。この量が系が異なっても同じになる。
光の場合 (⊿t)2=(⊿X)2+(⊿Y)2+(⊿Z)2 ( ∵ 光の速さが1だから )
光速不変の原理により (⊿ )2=(⊿
)2=(⊿
 )2+(⊿
)2+(⊿
 )2+(⊿
)2+(⊿
 )2 でもある。
)2 でもある。
◆ ⊿S2=ー(⊿t)2+(⊿X)2+(⊿Y)2+(⊿Z)2 ・・・・・・・・・・・・・・・ (3)
◆ ⊿ 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
・・・・・・・・・・・・・・・ (4)
)2
・・・・・・・・・・・・・・・ (4)
と間隔を定義する。
(⊿S2 は⊿Sの二乗という意味ではない。一つの記号である。⊿S2は正にもなるし負にもなる)
光の場合 ⊿S2=⊿ 2=0 である。
2=0 である。
光でない場合はローレンツ変換式により
故に光でない場合も間隔の不変性が成り立つ。今、tとXの二次元で証明したが四次元の場合も 同様に⊿S2=⊿ 2
が成り立つ。
付録:空間軸が回転している時のローレンツ変換を参照。
2
が成り立つ。
付録:空間軸が回転している時のローレンツ変換を参照。
事象の関係の分類
光の場合 (⊿t)2=(⊿X)2+(⊿Y)2+(⊿Z)2 ( ∵ 光の速さが1だから )
光速不変の原理により (⊿
 )2=(⊿
)2=(⊿
 )2+(⊿
)2+(⊿
 )2+(⊿
)2+(⊿
 )2 でもある。
)2 でもある。◆ ⊿S2=ー(⊿t)2+(⊿X)2+(⊿Y)2+(⊿Z)2 ・・・・・・・・・・・・・・・ (3)
◆ ⊿
 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
・・・・・・・・・・・・・・・ (4)
)2
・・・・・・・・・・・・・・・ (4)と間隔を定義する。
(⊿S2 は⊿Sの二乗という意味ではない。一つの記号である。⊿S2は正にもなるし負にもなる)
光の場合 ⊿S2=⊿
 2=0 である。
2=0 である。光でない場合はローレンツ変換式により
⊿ 2=ー⊿
2=ー⊿ 2+⊿
2+⊿ 2
=ーγ2(⊿t-V⊿X)2+γ2(⊿X-V⊿t)2
2
=ーγ2(⊿t-V⊿X)2+γ2(⊿X-V⊿t)2
=ー⊿t2+⊿X2=⊿S2
 2=ー⊿
2=ー⊿ 2+⊿
2+⊿ 2
=ーγ2(⊿t-V⊿X)2+γ2(⊿X-V⊿t)2
2
=ーγ2(⊿t-V⊿X)2+γ2(⊿X-V⊿t)2
=ー⊿t2+⊿X2=⊿S2
故に光でない場合も間隔の不変性が成り立つ。今、tとXの二次元で証明したが四次元の場合も 同様に⊿S2=⊿
 2
が成り立つ。
付録:空間軸が回転している時のローレンツ変換を参照。
2
が成り立つ。
付録:空間軸が回転している時のローレンツ変換を参照。事象の関係の分類
⊿S2が正ならば(空間部分の増分が⊿tよりも大きい)、空間的に離れているという。⊿S2が負ならば、時間的に離れているという。⊿S2がゼロなら(二つの事象が同じ光の世界線上にある)それらの事象は光的あるいはヌル的に離れているという。
 任意の特定の事象Ωから光的に離れている事象はΩを頂点とする円錐上にのる。左にこの円錐を示した。これをΩの光円錐と呼ぶ。光円錐の中の全ての事象はΩから時間的に離れており、その外にある事象は空間的に離れている。従って光円錐の中の全ての事象は至る所、時間的な方向に動いている世界線によってΩから到達する事が出来る。なにものも光速以上には動けないから、物理的な物体の全ての世界線は時間的な方向に動く。こうして光円錐の中の事象にはΩから物理的な物体が到達する事が出来るが、その外ではそうはならない。
任意の特定の事象Ωから光的に離れている事象はΩを頂点とする円錐上にのる。左にこの円錐を示した。これをΩの光円錐と呼ぶ。光円錐の中の全ての事象はΩから時間的に離れており、その外にある事象は空間的に離れている。従って光円錐の中の全ての事象は至る所、時間的な方向に動いている世界線によってΩから到達する事が出来る。なにものも光速以上には動けないから、物理的な物体の全ての世界線は時間的な方向に動く。こうして光円錐の中の事象にはΩから物理的な物体が到達する事が出来るが、その外ではそうはならない。
 任意の特定の事象Ωから光的に離れている事象はΩを頂点とする円錐上にのる。左にこの円錐を示した。これをΩの光円錐と呼ぶ。光円錐の中の全ての事象はΩから時間的に離れており、その外にある事象は空間的に離れている。従って光円錐の中の全ての事象は至る所、時間的な方向に動いている世界線によってΩから到達する事が出来る。なにものも光速以上には動けないから、物理的な物体の全ての世界線は時間的な方向に動く。こうして光円錐の中の事象にはΩから物理的な物体が到達する事が出来るが、その外ではそうはならない。
任意の特定の事象Ωから光的に離れている事象はΩを頂点とする円錐上にのる。左にこの円錐を示した。これをΩの光円錐と呼ぶ。光円錐の中の全ての事象はΩから時間的に離れており、その外にある事象は空間的に離れている。従って光円錐の中の全ての事象は至る所、時間的な方向に動いている世界線によってΩから到達する事が出来る。なにものも光速以上には動けないから、物理的な物体の全ての世界線は時間的な方向に動く。こうして光円錐の中の事象にはΩから物理的な物体が到達する事が出来るが、その外ではそうはならない。
5.不変双曲線と時空図の目盛付け
光速不変の原理により間隔が系に依らない事が分かった。この事を用いて座標軸の目盛付けを行う。t-X面だけを考える。ーt2+X2=ーa2 は双曲線であり、原点からの間隔がa2である全ての事象を通る。間隔の不変性からそれらの事象は の原点からも間隔 a2 をもち、従って
の原点からも間隔 a2 をもち、従って
ー 2+
2+ 2=ーa2 上にのる。この双曲線は時間軸を目盛付ける。ーt2+x2=b2 は空間軸を目盛付ける。
2=ーa2 上にのる。この双曲線は時間軸を目盛付ける。ーt2+x2=b2 は空間軸を目盛付ける。
 双曲線ーt2+x2=ーa2は事象①でt=aとなる。同様に事象②は
双曲線ーt2+x2=ーa2は事象①でt=aとなる。同様に事象②は 軸上にあるから
軸上にあるから =0であり、双曲線の方程式はー
=0であり、双曲線の方程式はー 2+
2+ 2=ーa2でもあるから、事象②で
2=ーa2でもあるから、事象②で =aとなる。
同様に双曲線 ーt2+x2=b2 は事象⑩で座標t=0, x=bをもち、事象⑪は座標
=aとなる。
同様に双曲線 ーt2+x2=b2 は事象⑩で座標t=0, x=bをもち、事象⑪は座標 =0,
=0,  =bをもつ。
=bをもつ。
具体的に a , bに 1 , 2 , 3を代入して図を描くと下図の様になる。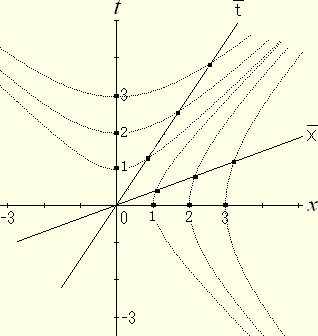
 の原点からも間隔 a2 をもち、従って
の原点からも間隔 a2 をもち、従ってー
 2+
2+ 2=ーa2 上にのる。この双曲線は時間軸を目盛付ける。ーt2+x2=b2 は空間軸を目盛付ける。
2=ーa2 上にのる。この双曲線は時間軸を目盛付ける。ーt2+x2=b2 は空間軸を目盛付ける。 双曲線ーt2+x2=ーa2は事象①でt=aとなる。同様に事象②は
双曲線ーt2+x2=ーa2は事象①でt=aとなる。同様に事象②は 軸上にあるから
軸上にあるから =0であり、双曲線の方程式はー
=0であり、双曲線の方程式はー 2+
2+ 2=ーa2でもあるから、事象②で
2=ーa2でもあるから、事象②で =aとなる。
同様に双曲線 ーt2+x2=b2 は事象⑩で座標t=0, x=bをもち、事象⑪は座標
=aとなる。
同様に双曲線 ーt2+x2=b2 は事象⑩で座標t=0, x=bをもち、事象⑪は座標 =0,
=0,  =bをもつ。
=bをもつ。具体的に a , bに 1 , 2 , 3を代入して図を描くと下図の様になる。

6.時間の遅れと固有時間
前節の時空図で系 の時計は事象②で時刻aを示すが系Sの時計では事象②は
の時計は事象②で時刻aを示すが系Sの時計では事象②は
時刻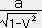 を示す。( ーt2+X2=ーa2 と X=Vtより )
を示す。( ーt2+X2=ーa2 と X=Vtより )
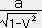 > aなので系Sにとっては系
> aなので系Sにとっては系 の時計はゆっくり進んでいるように見える。つまり
の時計はゆっくり進んでいるように見える。つまり
◆ t= ・・・・・・・・・・・・・・・ (5)
・・・・・・・・・・・・・・・ (5)
固有時間とは系 での時間の事である。系
での時間の事である。系 で静止している時計は⊿
で静止している時計は⊿ =⊿
=⊿ =⊿
=⊿ =0であり、固有時間を⊿τとすると
=0であり、固有時間を⊿τとすると
◆ ⊿S2=⊿ 2=ー⊿
2=ー⊿ 2=ー⊿τ2
・・・・・・・・・・・・・・・ (6)
2=ー⊿τ2
・・・・・・・・・・・・・・・ (6)
上の式より固有時間は間隔にマイナスを付けたものの平方根である事が分かる。固有時間⊿τを系Sでの座標の量で書くと次の様になる。
⊿τ=[(⊿t)2ー(⊿X)2ー(⊿Y)2ー(⊿Z)2]1/2=[(⊿t)2ーV2(⊿t)2]1/2
従って
◆ ⊿τ=⊿t ・・・・・・・・・・・・・・・ (7)
・・・・・・・・・・・・・・・ (7)
系Sの測った系 の時計は自分の時計よりもゆっくり進んでいる事が示された。この事は系
の時計は自分の時計よりもゆっくり進んでいる事が示された。この事は系 が系Sの時計を測ると自分の時計よりも速く進んでいる事を意味しないのだろうか? その事について考えてみる。
が系Sの時計を測ると自分の時計よりも速く進んでいる事を意味しないのだろうか? その事について考えてみる。
 先に事象②でSは自分の時計が
先に事象②でSは自分の時計が 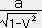 を指しているのに
を指しているのに の時計はaであると観測した。では
の時計はaであると観測した。では はSの時計をどの様に観測するであろうか。
はSの時計をどの様に観測するであろうか。 にとって同時の線は(イ)である。(
にとって同時の線は(イ)である。(  軸に平行で、双曲線の事象②での接線 )
軸に平行で、双曲線の事象②での接線 )  は同時の線(イ)がt軸と交わる事象③を S の時刻と観測する。そ れは簡単な計算よりa
は同時の線(イ)がt軸と交わる事象③を S の時刻と観測する。そ れは簡単な計算よりa となる。
となる。
a > a なので系
なので系 にとっては系Sの時計はゆっくり進んでいるように見える。従ってお互いが相手の時計はゆっくり進んでいると観測する。
ミンコフスキーの時空図で分かる通り系Sの現在は系
にとっては系Sの時計はゆっくり進んでいるように見える。従ってお互いが相手の時計はゆっくり進んでいると観測する。
ミンコフスキーの時空図で分かる通り系Sの現在は系 にとっては現在でないし、系
にとっては現在でないし、系 の現在は系Sにとっては現在でないのである。
の現在は系Sにとっては現在でないのである。
では が瞬間的に停止したとしよう(瞬間的に停止できると仮定して)。
即ち
が瞬間的に停止したとしよう(瞬間的に停止できると仮定して)。
即ち の慣性系が瞬間的に変わる。
の慣性系が瞬間的に変わる。
下の図にその時の時空図が描かれている。
 の
の 軸と
軸と 軸がSのt軸、X軸と同じ方向を向いている。(停止したのだからSと同じ慣性系になる)
軸がSのt軸、X軸と同じ方向を向いている。(停止したのだからSと同じ慣性系になる)
 の同時の線が(イ)から(ア)に変わり、事象③が①に変わるのである。 従って
の同時の線が(イ)から(ア)に変わり、事象③が①に変わるのである。 従って はSの時刻をa
はSの時刻をa と観測していたのが一瞬にして
と観測していたのが一瞬にして 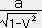 に変わるのである。(
に変わるのである。(  の時刻は a )
の時刻は a )
宇宙船が光速の90%で周回していると仮定すると、そこに乗船している宇宙飛行士は宇宙飛行士の時間で1年経過後に地球に帰還した時、地上では2.29年経過した事になる。((5)の式の右辺に =1、V=0.9を代入して計算するとt=2.29 )
=1、V=0.9を代入して計算するとt=2.29 )
時間の遅れの正しさは、高速で運動している素粒子ミュー粒子の観測で分かっている。ミュー粒子の半減期は1.5x10 -6 秒で、上空の大気、約20000mの所で発生する。ミュー粒子が光速で運動しているとしても、 相対論を考慮しない場合は3x108x1.5x10-6=450mしか走れず地上に到達しない。 しかし実際には地上に到達してる。ミュー粒子が速度0.9998で運動していて、時間の遅れを適用すると20000m( 0.9998x3x108x1.5x10ー6・img SRC="SF/05/003.jpg" class=f>= 20124m )走れ、地上に到達出来る。
そのほか、グローバル・ポジショニング・システム (GPS)では時間の補正を行っている。その補正をしないと位置情報が1日に約11kmもずれてしまう。何故時間の補正を行うかというと、GPS衛星は秒速約4kmと高速で運動しているため時間の遅れが生じる。一方、GPS衛星は約2万kmの高さに位置するため、地球の重力場の影響が地上より小さいので地上よりも時間の進み方が速くなる。そういう理由で時間の補正を行う。
 の時計は事象②で時刻aを示すが系Sの時計では事象②は
の時計は事象②で時刻aを示すが系Sの時計では事象②は時刻
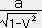 を示す。( ーt2+X2=ーa2 と X=Vtより )
を示す。( ーt2+X2=ーa2 と X=Vtより )
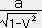 > aなので系Sにとっては系
> aなので系Sにとっては系 の時計はゆっくり進んでいるように見える。つまり
の時計はゆっくり進んでいるように見える。つまり◆ t=
 ・・・・・・・・・・・・・・・ (5)
・・・・・・・・・・・・・・・ (5)固有時間とは系
 での時間の事である。系
での時間の事である。系 で静止している時計は⊿
で静止している時計は⊿ =⊿
=⊿ =⊿
=⊿ =0であり、固有時間を⊿τとすると
=0であり、固有時間を⊿τとすると◆ ⊿S2=⊿
 2=ー⊿
2=ー⊿ 2=ー⊿τ2
・・・・・・・・・・・・・・・ (6)
2=ー⊿τ2
・・・・・・・・・・・・・・・ (6)上の式より固有時間は間隔にマイナスを付けたものの平方根である事が分かる。固有時間⊿τを系Sでの座標の量で書くと次の様になる。
⊿τ=[(⊿t)2ー(⊿X)2ー(⊿Y)2ー(⊿Z)2]1/2=[(⊿t)2ーV2(⊿t)2]1/2
従って
◆ ⊿τ=⊿t
 ・・・・・・・・・・・・・・・ (7)
・・・・・・・・・・・・・・・ (7)
系Sの測った系
 の時計は自分の時計よりもゆっくり進んでいる事が示された。この事は系
の時計は自分の時計よりもゆっくり進んでいる事が示された。この事は系 が系Sの時計を測ると自分の時計よりも速く進んでいる事を意味しないのだろうか? その事について考えてみる。
が系Sの時計を測ると自分の時計よりも速く進んでいる事を意味しないのだろうか? その事について考えてみる。
 先に事象②でSは自分の時計が
先に事象②でSは自分の時計が 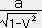 を指しているのに
を指しているのに の時計はaであると観測した。では
の時計はaであると観測した。では はSの時計をどの様に観測するであろうか。
はSの時計をどの様に観測するであろうか。 にとって同時の線は(イ)である。(
にとって同時の線は(イ)である。(  軸に平行で、双曲線の事象②での接線 )
軸に平行で、双曲線の事象②での接線 )  は同時の線(イ)がt軸と交わる事象③を S の時刻と観測する。そ れは簡単な計算よりa
は同時の線(イ)がt軸と交わる事象③を S の時刻と観測する。そ れは簡単な計算よりa となる。
となる。a > a
 なので系
なので系 にとっては系Sの時計はゆっくり進んでいるように見える。従ってお互いが相手の時計はゆっくり進んでいると観測する。
ミンコフスキーの時空図で分かる通り系Sの現在は系
にとっては系Sの時計はゆっくり進んでいるように見える。従ってお互いが相手の時計はゆっくり進んでいると観測する。
ミンコフスキーの時空図で分かる通り系Sの現在は系 にとっては現在でないし、系
にとっては現在でないし、系 の現在は系Sにとっては現在でないのである。
の現在は系Sにとっては現在でないのである。
では
 が瞬間的に停止したとしよう(瞬間的に停止できると仮定して)。
即ち
が瞬間的に停止したとしよう(瞬間的に停止できると仮定して)。
即ち の慣性系が瞬間的に変わる。
の慣性系が瞬間的に変わる。下の図にその時の時空図が描かれている。
 の
の 軸と
軸と 軸がSのt軸、X軸と同じ方向を向いている。(停止したのだからSと同じ慣性系になる)
軸がSのt軸、X軸と同じ方向を向いている。(停止したのだからSと同じ慣性系になる) の同時の線が(イ)から(ア)に変わり、事象③が①に変わるのである。 従って
の同時の線が(イ)から(ア)に変わり、事象③が①に変わるのである。 従って はSの時刻をa
はSの時刻をa と観測していたのが一瞬にして
と観測していたのが一瞬にして 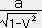 に変わるのである。(
に変わるのである。(  の時刻は a )
の時刻は a )
宇宙船が光速の90%で周回していると仮定すると、そこに乗船している宇宙飛行士は宇宙飛行士の時間で1年経過後に地球に帰還した時、地上では2.29年経過した事になる。((5)の式の右辺に
 =1、V=0.9を代入して計算するとt=2.29 )
=1、V=0.9を代入して計算するとt=2.29 )時間の遅れの正しさは、高速で運動している素粒子ミュー粒子の観測で分かっている。ミュー粒子の半減期は1.5x10 -6 秒で、上空の大気、約20000mの所で発生する。ミュー粒子が光速で運動しているとしても、 相対論を考慮しない場合は3x108x1.5x10-6=450mしか走れず地上に到達しない。 しかし実際には地上に到達してる。ミュー粒子が速度0.9998で運動していて、時間の遅れを適用すると20000m( 0.9998x3x108x1.5x10ー6・img SRC="SF/05/003.jpg" class=f>= 20124m )走れ、地上に到達出来る。
そのほか、グローバル・ポジショニング・システム (GPS)では時間の補正を行っている。その補正をしないと位置情報が1日に約11kmもずれてしまう。何故時間の補正を行うかというと、GPS衛星は秒速約4kmと高速で運動しているため時間の遅れが生じる。一方、GPS衛星は約2万kmの高さに位置するため、地球の重力場の影響が地上より小さいので地上よりも時間の進み方が速くなる。そういう理由で時間の補正を行う。
7.ローレンツ収縮(空間の収縮)
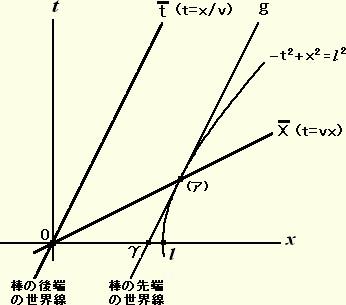 物体の長さを測るためには、物体の先端と後端を同時に測らねばならない。系
物体の長さを測るためには、物体の先端と後端を同時に測らねばならない。系 で静止している長さ l の棒((ア)-0)の両端の世界線を左の図に示した。系Sではその長さは棒の両端の世界線がSの同時刻の時のX座標の差として観測される。即ち直線
で静止している長さ l の棒((ア)-0)の両端の世界線を左の図に示した。系Sではその長さは棒の両端の世界線がSの同時刻の時のX座標の差として観測される。即ち直線 とgがt=0でX軸と交わるX座標の差(γ-0)で観測される。
事象(ア)の系Sでの座標を(tξ,Xξ)とすると、不変双曲線
とgがt=0でX軸と交わるX座標の差(γ-0)で観測される。
事象(ア)の系Sでの座標を(tξ,Xξ)とすると、不変双曲線ーt2+X2=l 2 と直線 t =VX の交点より
tξ=Vl/
 , Xξ=l/
, Xξ=l/
である。直線gの傾きは1/Vであるので直線gの方程式は
t=(X-Xξ)/V+tξ
上記の式にt=0,tξ,Xξを代入してXの値を求めるとX=l
 。即ちγの系Sでの座標は
。即ちγの系Sでの座標はt=0 , X=l
 ・・・・・・・・・・・・ (8)
・・・・・・・・・・・・ (8)である。故に運動の方向に
 の割合で縮む。これをローレンツ収縮と言う。時間の遅れがそうであったようにこの場合も運動する慣性系では空間そのものが収縮すると考 えねばならない。
の割合で縮む。これをローレンツ収縮と言う。時間の遅れがそうであったようにこの場合も運動する慣性系では空間そのものが収縮すると考 えねばならない。
8.速 度 の 合 成 則
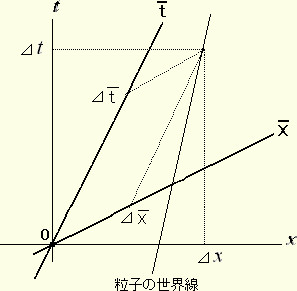 ある粒子が
ある粒子が の
の 軸方向に速度Gで動いている。即ち G=⊿
軸方向に速度Gで動いている。即ち G=⊿ /⊿
/⊿ 別の系Sではその速度は W=⊿X/⊿tで、⊿Xと⊿tをローレンツ変換より求めることが出来る。
別の系Sではその速度は W=⊿X/⊿tで、⊿Xと⊿tをローレンツ変換より求めることが出来る。 が速度VでSに対して動いているとすると
が速度VでSに対して動いているとすると⊿X=ε(⊿
 +V⊿
+V⊿ ), ⊿t=ε(⊿
), ⊿t=ε(⊿  +V⊿
+V⊿ )
)(ε=
 )
)従ってW=⊿X/⊿t=(⊿
 +V⊿
+V⊿ )/(⊿
)/(⊿ +V⊿
+V⊿ )
)=(⊿
 /⊿
/⊿ +V)/(1+V⊿
+V)/(1+V⊿ /⊿
/⊿ )
)◆ W =(G+V)/(1+GV) ・・・・・・・・・・・・ (9)
これがアインシュタインの速度の合成則である。上の式に於いてG=V=1(光の速度)と置いてもW=1であることが分る。つまり光の速度で走っている物体より光を発しても地上に静止している観測者は光の速度にしか見えないという事になる。
1.特殊相対論の基本原理(1)光速不変の原理で述べた疑問の解答は
G=(150x1000/3600)/(3x108)=1.39x10-7
V=(100x1000/3600)/(3x108)=9.26x10-8
で GV=1.29x10ー14 0 となり、地上に静止している観測者は時速250kmと観測するのである。
0 となり、地上に静止している観測者は時速250kmと観測するのである。
G 《 1 ,V 《 1なら W=G+V となる。これは我々が日常経験しているガリレオの速度の合成則である。
V=(100x1000/3600)/(3x108)=9.26x10-8
で GV=1.29x10ー14
 0 となり、地上に静止している観測者は時速250kmと観測するのである。
0 となり、地上に静止している観測者は時速250kmと観測するのである。
9.物質=エネルギー(E=MC2)
この宇宙が始まった時、物質は全く存在せずエネルギーだけが存在した。そのエネルギーから素粒子が出来、素粒子から物質が出来たのだから、エネルギーと物質は等価であると考えるのは極く当り前で、自然な事かもしれない。
(1)エネルギーと力の定義
エネルギーとは仕事をなしうるもののことである。物体に力Fが働いて物体が力の方向にSだけ動いた時、その力は物体に仕事をしたという。仕事の大きさは力の大きさと物体が動いた距離との積FSで表わされる。
力Fは運動量の時間に対する変化率で定義される。
 M0:物体の静止質量 V:速度
M0:物体の静止質量 V:速度
 M0:物体の静止質量 V:速度
M0:物体の静止質量 V:速度(2)三元速度及び四元速度、四元運動量
イ)三元速度
ロ)四元速度、四元運動量
ミンコフスキーの時空に於ける四次元幾何学では速度は粒子の世界線に
接するベクトルであり、粒子の座標は 固有時間τの関数として表される。
四元速度を Ut, Ux, Uy, Uzとすれば
Ut=dt/dτ , Ux=dx/dτ , Uy=dy/dτ , Uz=dz/dτ
時間の遅れにより dτ= dt の関係があるので
dt の関係があるので
Ut= , Ux=
, Ux= Vx , Uy=
Vx , Uy= Vy , Uz =
Vy , Uz = Vz
Vz
四元運動量を Pt, Px, Py, Pzとすれば
Pt=M0Ut , Px=M0Ux , Py=M0Uy , Pz =M0Uz
従って
Pt= , Px=
, Px=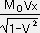 , Py=
, Py=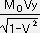 , Pz=
, Pz=
ガリレオの三次元幾何学では速度は粒子の軌道に接するベクトルである。
粒子の座標を X(t) , Y(t) , Z(t)
三元速度を Vx , Vy , Vzとすれば
Vx=dX/dt , Vy=dY/dt , Vz=dZ/dt
粒子の座標を X(t) , Y(t) , Z(t)
三元速度を Vx , Vy , Vzとすれば
Vx=dX/dt , Vy=dY/dt , Vz=dZ/dt
ロ)四元速度、四元運動量
ミンコフスキーの時空に於ける四次元幾何学では速度は粒子の世界線に
接するベクトルであり、粒子の座標は 固有時間τの関数として表される。
四元速度を Ut, Ux, Uy, Uzとすれば
Ut=dt/dτ , Ux=dx/dτ , Uy=dy/dτ , Uz=dz/dτ
時間の遅れにより dτ=
 dt の関係があるので
dt の関係があるのでUt=
 , Ux=
, Ux= Vx , Uy=
Vx , Uy= Vy , Uz =
Vy , Uz = Vz
Vz四元運動量を Pt, Px, Py, Pzとすれば
Pt=M0Ut , Px=M0Ux , Py=M0Uy , Pz =M0Uz
従って
Pt=
 , Px=
, Px=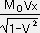 , Py=
, Py=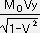 , Pz=
, Pz=
(3)微小エネルギーの計算
微小エネルギーをdEとすると(1)の定義により
dE=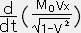 dx+
dx+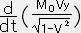 dy+
dy+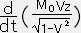 dz
dz
=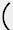
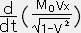 Vx+
Vx+ 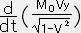 Vy+
Vy+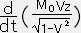 Vz
Vz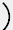 dt
dt
( ∵ dx=Vxdt , dy=Vydt , dz=Vzdt だから )
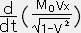 Vx ,
Vx ,
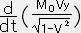 Vy ,
Vy ,
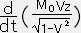 Vz をそれぞれ計算すると
Vz をそれぞれ計算すると
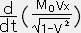 Vx=
Vx=

・・・①
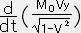 Vy=
Vy=
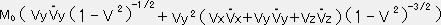
・・・②
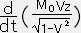 Vz=
Vz=
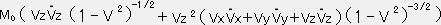
・・・③
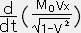 dx+
dx+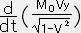 dy+
dy+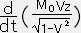 dz
dz =
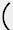
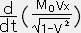 Vx+
Vx+ 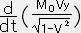 Vy+
Vy+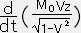 Vz
Vz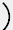 dt
dt( ∵ dx=Vxdt , dy=Vydt , dz=Vzdt だから )
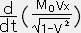 Vx ,
Vx ,
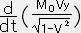 Vy ,
Vy ,
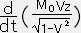 Vz をそれぞれ計算すると
Vz をそれぞれ計算すると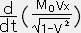 Vx=
Vx=

・・・①
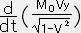 Vy=
Vy=
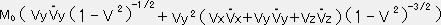
・・・②
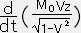 Vz=
Vz=
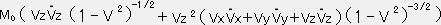
・・・③
ここで
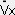 =dVx/dt,
=dVx/dt, 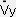 =dVy/d t,
=dVy/d t, 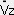 =dVz/dt,
V2=Vx2+Vy2+Vz2
=dVz/dt,
V2=Vx2+Vy2+Vz2
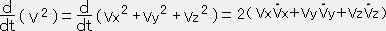 である。
である。
①, ②, ③ をそれぞれ加え整理すると
dE=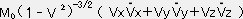 dt ・ ・・④
dt ・ ・・④
一方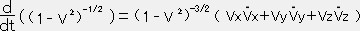 であるから
であるから
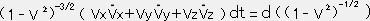 ・・・⑤
④ と ⑤ より dE=
・・・⑤
④ と ⑤ より dE=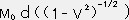 が成り立つ
が成り立つ
両辺を積分すると
◆ E=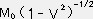 ・・・・・・・・・・・・・・・ (10)
・・・・・・・・・・・・・・・ (10)
従って上記の式より 「物質=エネルギー」 である事が分かる。V=0 なら
E=M0である。こ れは 物質が静止していてもエネルギーが存在している 事を意味している。 V≠0 なら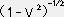 > 1 だから
> 1 だから 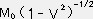 > M0 で運動している物質は質量が増加している
事を表わす。V=0.9(光速の90%)で運動している物質の質量は静止質量の約2.29倍になる。
> M0 で運動している物質は質量が増加している
事を表わす。V=0.9(光速の90%)で運動している物質の質量は静止質量の約2.29倍になる。
1gの物質(=W0)が完全にエネルギーに変換された場合を計算してみる。
SI単位系ではエネルギーの単位はKg・m2・S-2である。
SI単位から自然単位に変換した時S-2を(3x108m)-2 に置き換えたのだから自然単位をSI単位で表す時は(3x108mS-1 )2を掛けてやればよい。従って
W0=1x10-3x(3x108)2Kgm2 S-2である。
石炭1トンを燃焼して発生する熱量は約6x106Kcal=6x106x4185Kg m2S-2 である。
W0=(1x10-3x(3x108)2)/(6x106 x4185)=3584
物質1gが完全にエネルギーに変換されると石炭3584トンを燃焼して発生する熱量に相当する事になる。
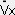 =dVx/dt,
=dVx/dt, 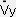 =dVy/d t,
=dVy/d t, 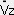 =dVz/dt,
V2=Vx2+Vy2+Vz2
=dVz/dt,
V2=Vx2+Vy2+Vz2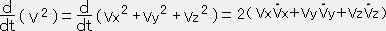 である。
である。①, ②, ③ をそれぞれ加え整理すると
dE=
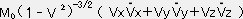 dt ・ ・・④
dt ・ ・・④
一方
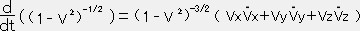 であるから
であるから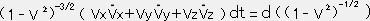 ・・・⑤
④ と ⑤ より dE=
・・・⑤
④ と ⑤ より dE=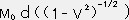 が成り立つ
が成り立つ両辺を積分すると
◆ E=
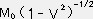 ・・・・・・・・・・・・・・・ (10)
・・・・・・・・・・・・・・・ (10)従って上記の式より 「物質=エネルギー」 である事が分かる。V=0 なら
E=M0である。こ れは 物質が静止していてもエネルギーが存在している 事を意味している。 V≠0 なら
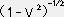 > 1 だから
> 1 だから 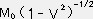 > M0 で運動している物質は質量が増加している
事を表わす。V=0.9(光速の90%)で運動している物質の質量は静止質量の約2.29倍になる。
> M0 で運動している物質は質量が増加している
事を表わす。V=0.9(光速の90%)で運動している物質の質量は静止質量の約2.29倍になる。1gの物質(=W0)が完全にエネルギーに変換された場合を計算してみる。
SI単位系ではエネルギーの単位はKg・m2・S-2である。
SI単位から自然単位に変換した時S-2を(3x108m)-2 に置き換えたのだから自然単位をSI単位で表す時は(3x108mS-1 )2を掛けてやればよい。従って
W0=1x10-3x(3x108)2Kgm2 S-2である。
石炭1トンを燃焼して発生する熱量は約6x106Kcal=6x106x4185Kg m2S-2 である。
W0=(1x10-3x(3x108)2)/(6x106 x4185)=3584
物質1gが完全にエネルギーに変換されると石炭3584トンを燃焼して発生する熱量に相当する事になる。
付録1:SI単位系から自然単位系へ
SI単位から自然単位へ変換するには、SI単位に現れるS(=秒)をmにする。最初に定義したように
1s=3x108mである。下記の例では、最後の式が自然単位系である。
★ 例1:10J=10Kg・m2・s-2
10J=10Kg・m2・(3x108m)-2=1.1x10-16Kg
★ 例2:100W=100Kg・m2・s-3
100W=100Kg・m2・(3x108m)-3=3.7x10-24Kg・m-1
★ 例3:プランク定数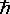 =1.05x10-34J・s=1.05x10-34Kg・m2・s-1
=1.05x10-34J・s=1.05x10-34Kg・m2・s-1
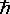 =1.05x10-34Kg・m2・(3x108m)-1=3.5x10-43Kg・m
=1.05x10-34Kg・m2・(3x108m)-1=3.5x10-43Kg・m
★ 例4:車の速度 V=30m・s-1
V=30m・s-1=30mx(3x108m)-1=10-7
★ 例5:車の運動量=3x104Kgm・s-1
車の運動量=3x104Kgm・s-1=3x104Kgmx(3x108m)-1=10-4Kg
★ 例6:1気圧=105N・m-2=105Kg・m-1・s-2
1気圧=105Kg・m-1・s-2=105Kg・m-1x(3x108m)-2=1.1x10-12Kg・m-3
★ 例7:水の密度=103Kg・m-3
★ 例8:光度106J・cm-2・s-1=106Kg・m2・s-2x(10-2m)-2・s-1=1010Kg・s-3
光度106J・cm-2・s-1=1010Kg・s-3=1010Kgx(3x108m)-3=3.7x10-16Kg・m-3
★ 例1:10J=10Kg・m2・s-2
10J=10Kg・m2・(3x108m)-2=1.1x10-16Kg
★ 例2:100W=100Kg・m2・s-3
100W=100Kg・m2・(3x108m)-3=3.7x10-24Kg・m-1
★ 例3:プランク定数
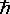 =1.05x10-34J・s=1.05x10-34Kg・m2・s-1
=1.05x10-34J・s=1.05x10-34Kg・m2・s-1
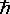 =1.05x10-34Kg・m2・(3x108m)-1=3.5x10-43Kg・m
=1.05x10-34Kg・m2・(3x108m)-1=3.5x10-43Kg・m★ 例4:車の速度 V=30m・s-1
V=30m・s-1=30mx(3x108m)-1=10-7
★ 例5:車の運動量=3x104Kgm・s-1
車の運動量=3x104Kgm・s-1=3x104Kgmx(3x108m)-1=10-4Kg
★ 例6:1気圧=105N・m-2=105Kg・m-1・s-2
1気圧=105Kg・m-1・s-2=105Kg・m-1x(3x108m)-2=1.1x10-12Kg・m-3
★ 例7:水の密度=103Kg・m-3
★ 例8:光度106J・cm-2・s-1=106Kg・m2・s-2x(10-2m)-2・s-1=1010Kg・s-3
光度106J・cm-2・s-1=1010Kg・s-3=1010Kgx(3x108m)-3=3.7x10-16Kg・m-3
付録2:自然単位系からSI単位系へ
自然単位からSI単位へ変換するには、その物理量がSI単位ではどういう次元であるかを確認し、自然単位に現れるmをS(=秒)にする。1m=(3x108)-1sである。下記の例では最後の式がSI単位系である。
★ 例1:速度V=10-2 速度のSI単位はm・s-1
1=3x108ms-1であるから V=10-2x1=3x106m・s-1
★ 例2:圧力1019Kg・m-3 圧力のSI単位はKg・m-1・s-2
m-3=m-1・m-2であるから
圧力1019Kg・m-3=1019Kg・m-1x((3x108)-1s)-2=9x1035Kg・m-1・s-2
★ 例3:時間t=1018m 時間のSI単位はs
時間t=1018m=1018x(3x108)-1s=3.3x109s
★ 例4:エネルギー密度u=1Kg・m-3 エネルギー密度のSI単位はKg・m-1・s-2
m-3=m-1・m-2であるから
エネルギー密度u=1Kg・m-3=1Kg・m-1x((3x108)-1s)-2=9x1016Kg・m-1・s-2
★ 例5:加速度=10m-1 加速度のSI単位はm・s-2
m-1=m1・m-2であるから
加速度=10m-1=10m1x((3x108)-1s)-2=9x1017m・s-2
★ 例6:物質=1Kg エネルギーのSI単位はKg・m-2・s-2
12=9x1016m2s-2であるから
物質=1Kg=1Kgx12=9x1016Kg・m2・s-2
★ 例1:速度V=10-2 速度のSI単位はm・s-1
1=3x108ms-1であるから V=10-2x1=3x106m・s-1
★ 例2:圧力1019Kg・m-3 圧力のSI単位はKg・m-1・s-2
m-3=m-1・m-2であるから
圧力1019Kg・m-3=1019Kg・m-1x((3x108)-1s)-2=9x1035Kg・m-1・s-2
★ 例3:時間t=1018m 時間のSI単位はs
時間t=1018m=1018x(3x108)-1s=3.3x109s
★ 例4:エネルギー密度u=1Kg・m-3 エネルギー密度のSI単位はKg・m-1・s-2
m-3=m-1・m-2であるから
エネルギー密度u=1Kg・m-3=1Kg・m-1x((3x108)-1s)-2=9x1016Kg・m-1・s-2
★ 例5:加速度=10m-1 加速度のSI単位はm・s-2
m-1=m1・m-2であるから
加速度=10m-1=10m1x((3x108)-1s)-2=9x1017m・s-2
★ 例6:物質=1Kg エネルギーのSI単位はKg・m-2・s-2
12=9x1016m2s-2であるから
物質=1Kg=1Kgx12=9x1016Kg・m2・s-2
付録3:空間軸が回転している時のローレンツ変換
U方向への速度Vのブーストと呼ばれるものは
「2.ガリレイ変換とローレンツ変換」より
 =
=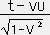 ,
, 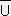 =
=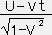 である。
である。
UのX軸方向、Y軸方向、Z軸方向への一般的なローレンツ変換行列を求める。UがX軸となる直交座標系Oエー XエYエZエを設定する(原点は直交座標系OーXYZと一致)。変換行列は次の手順で求める。
(1)直交座標系OーXYZの座標値を直交座標系Oエー XエYエZエの座標値に変換する。 ・・・・・ C
(2)Xエ軸方向(=U方向)へのローレンツ変換 ・・・・・ L
(3)直交座標系Oエー XエYエZエの座標値を直交座標系OーXYZの座標値に変換する。 ・・・・・ C-1 (Cの逆行列)
(1)(2)(3)を順に施せば一般的なローレンツ変換行列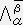 は
は 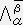 = C-1LCで求まる。
= C-1LCで求まる。
(1) OーXYZの座標値をOエー XエYエZエの座標値に変換するCを求める。
 Xエ軸はUと同じ方向。Xエ軸とX軸、Y軸、Z軸の成す角度をφ、θ、ψとするとXエ軸の方向余弦 l ,m ,nは
Xエ軸はUと同じ方向。Xエ軸とX軸、Y軸、Z軸の成す角度をφ、θ、ψとするとXエ軸の方向余弦 l ,m ,nは
l=cosφ=Vx/V
m=cosθ=Vy/V
n=cosψ=Vz/V
同様にYエ軸の方向余弦を lエ,mエ,nエ Zエ軸の方向余弦を l″,m″,n″とすると変換Cは

(2) Xエ軸方向へのローレンツ変換
前述のU方向へのローレンツ変換の結果を使用する。(5)(6)よりLを行列で表現すると

CにU方向(=Xエ軸方向)へのローレンツ変換を施すとLCは

(3) Oエー XエYエZエの座標値をOーXYZの座標値に変換
 =
=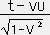 ,
, 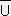 =
=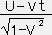 である。
である。UのX軸方向、Y軸方向、Z軸方向への一般的なローレンツ変換行列を求める。UがX軸となる直交座標系Oエー XエYエZエを設定する(原点は直交座標系OーXYZと一致)。変換行列は次の手順で求める。
(1)直交座標系OーXYZの座標値を直交座標系Oエー XエYエZエの座標値に変換する。 ・・・・・ C
(2)Xエ軸方向(=U方向)へのローレンツ変換 ・・・・・ L
(3)直交座標系Oエー XエYエZエの座標値を直交座標系OーXYZの座標値に変換する。 ・・・・・ C-1 (Cの逆行列)
(1)(2)(3)を順に施せば一般的なローレンツ変換行列
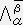 は
は 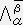 = C-1LCで求まる。
= C-1LCで求まる。(1) OーXYZの座標値をOエー XエYエZエの座標値に変換するCを求める。
 Xエ軸はUと同じ方向。Xエ軸とX軸、Y軸、Z軸の成す角度をφ、θ、ψとするとXエ軸の方向余弦 l ,m ,nは
Xエ軸はUと同じ方向。Xエ軸とX軸、Y軸、Z軸の成す角度をφ、θ、ψとするとXエ軸の方向余弦 l ,m ,nはl=cosφ=Vx/V
m=cosθ=Vy/V
n=cosψ=Vz/V
同様にYエ軸の方向余弦を lエ,mエ,nエ Zエ軸の方向余弦を l″,m″,n″とすると変換Cは

(2) Xエ軸方向へのローレンツ変換
前述のU方向へのローレンツ変換の結果を使用する。(5)(6)よりLを行列で表現すると

CにU方向(=Xエ軸方向)へのローレンツ変換を施すとLCは

(3) Oエー XエYエZエの座標値をOーXYZの座標値に変換
Cの転置行列Ctを作り、CCtを計算するとCCt=E(Eは単位行列)となるのでCtは逆行列でもある。(C-1=Ct ∵
l2+m2+n2=1, lエ2+mエ2+nエ2=1, l″2+m″2+n″2=1 で XエYエZエは互いに直交しているから llエ+mmエ+nnエ=0, lエl″+mエm″+nエn″=0, ll″+mm″+nn″=0 だから CCt=E)
C-1LCを計算すると
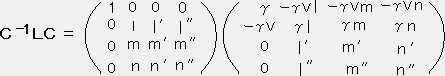
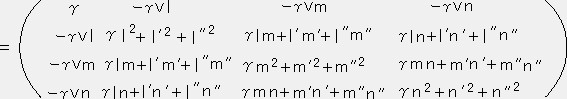
系Oエー XエYエZエから見たX軸の方向余弦はl ,lエ,l″ Y軸の方向余弦はm ,mエ,m″ Z軸の方向余弦はn ,nエ,n″だから次の式が成り立つ。
l2+lエ2+l″2=1 → lエ2+l″2= 1-l2
m2+mエ2+m″2=1 → mエ2+m″2= 1-m2
n2+nエ2+n″2=1 → nエ2+n″2= 1-n2
XYZは互いに直交しているから
lm+lエmエ+l″m″=0 → lエmエ+l″m″= -lm
ln+lエnエ+l″n″=0 → lエnエ+l″n″= -ln
mn+mエnエ+m″n″=0 → mエnエ+m″n″= -mn
上記の結果からC-1LCは

l=Vx/V m=Vy/V n=Vz/Vであったから、系 S から系 への一般的なローレンツ変換行列
への一般的なローレンツ変換行列 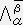 は
は
∴
次に空間軸が回転している場合でも間隔の不変性が成り立つ事を証明する。 系 での成分は
での成分は
 =
= X0+
X0+ X1+
X1+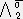 X2+
X2+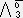 X3
X3
 =
=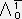 X0+
X0+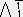 X1+
X1+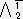 X2+
X2+ X3
X3
 =
=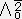 X0+
X0+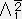 X1+
X1+ X2+
X2+ X3
X3
 =
=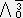 X0+
X0+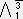 X1+
X1+ X2+
X2+ X3 である。
X3 である。
系 での間隔⊿
での間隔⊿ 2は
2は
(⊿X0)2の係数はー1、(⊿X1)2,(⊿X2)2,(⊿X3)2の係数は1、その他の項の係数は0になる。従って
系 から系 S への一般的なローレンツ変換行列
から系 S への一般的なローレンツ変換行列 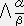 はV ,Vx ,Vy ,VzをーV ,ーVx ,ーVy ,ーVzに変えた次式になる。
はV ,Vx ,Vy ,VzをーV ,ーVx ,ーVy ,ーVzに変えた次式になる。

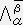 と
と 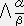 の掛け算を行うと単位行列になるので
の掛け算を行うと単位行列になるので 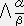 は
は 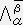 の逆行列である事が分かる。
の逆行列である事が分かる。
C-1LCを計算すると
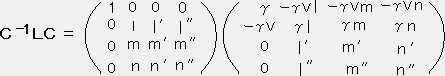
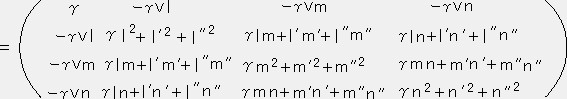
系Oエー XエYエZエから見たX軸の方向余弦はl ,lエ,l″ Y軸の方向余弦はm ,mエ,m″ Z軸の方向余弦はn ,nエ,n″だから次の式が成り立つ。
l2+lエ2+l″2=1 → lエ2+l″2= 1-l2
m2+mエ2+m″2=1 → mエ2+m″2= 1-m2
n2+nエ2+n″2=1 → nエ2+n″2= 1-n2
XYZは互いに直交しているから
lm+lエmエ+l″m″=0 → lエmエ+l″m″= -lm
ln+lエnエ+l″n″=0 → lエnエ+l″n″= -ln
mn+mエnエ+m″n″=0 → mエnエ+m″n″= -mn
上記の結果からC-1LCは

l=Vx/V m=Vy/V n=Vz/Vであったから、系 S から系
 への一般的なローレンツ変換行列
への一般的なローレンツ変換行列 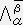 は
は∴
次に空間軸が回転している場合でも間隔の不変性が成り立つ事を証明する。 系
 での成分は
での成分は =
= X0+
X0+ X1+
X1+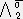 X2+
X2+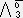 X3
X3 =
=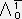 X0+
X0+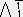 X1+
X1+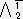 X2+
X2+ X3
X3 =
=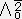 X0+
X0+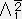 X1+
X1+ X2+
X2+ X3
X3 =
=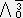 X0+
X0+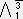 X1+
X1+ X2+
X2+ X3 である。
X3 である。 での間隔⊿
での間隔⊿ 2は
2は
⊿ 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
)2
上記の計算で、(⊿X0)2,(⊿X1)2,(⊿X2)2,(⊿X3)2,⊿X0⊿X1,⊿X0⊿X2,⊿X0⊿X3,⊿X1⊿X2
,⊿X1⊿X3,⊿X2⊿X3の項にそれぞれまとめると 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
)2
(⊿X0)2の係数はー1、(⊿X1)2,(⊿X2)2,(⊿X3)2の係数は1、その他の項の係数は0になる。従って
⊿ 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
)2
=ー(⊿X0)2+(⊿X1)2+(⊿X2)2+(⊿X3)2
=ー(⊿t)2+(⊿x)2+(⊿y)2+(⊿z)2
=⊿S2
故に空間軸が回転している場合でも間隔の不変性が成り立つ。 2=ー(⊿
2=ー(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2+(⊿
)2+(⊿ )2
)2=ー(⊿X0)2+(⊿X1)2+(⊿X2)2+(⊿X3)2
=ー(⊿t)2+(⊿x)2+(⊿y)2+(⊿z)2
=⊿S2
系
 から系 S への一般的なローレンツ変換行列
から系 S への一般的なローレンツ変換行列 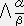 はV ,Vx ,Vy ,VzをーV ,ーVx ,ーVy ,ーVzに変えた次式になる。
はV ,Vx ,Vy ,VzをーV ,ーVx ,ーVy ,ーVzに変えた次式になる。
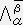 と
と 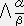 の掛け算を行うと単位行列になるので
の掛け算を行うと単位行列になるので 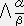 は
は 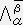 の逆行列である事が分かる。
の逆行列である事が分かる。