�e���\�����
< �ڎ��� >
���x�A�͂Ȃǂ̗l�ɑ傫���ƕ�����L����x�N�g���i�P�K�̃e���\���ł͂��邪�j�͕�����Ղ����A�e���\���Ƃ������̂͒��ϓI�ɗ������ɂ������̂ł���B���W�n�ɂ��e���\���̐����͕ω����邪���̒l�͕ς��Ȃ��A�܂���W�n�͕ς���Ă��A���̂̏�Ԃ���͕ω����Ȃ��̂��e���\���ł���B
�P. �e���\���̒�`
�^�C�v�i�l�C�m�j�̃e���\���Ƃ́A�l����`���Ƃm�̃x�N�g����ϐ��Ƃ�������ւ̊��� �A���̂��̕ϐ��ɂ��Đ��`�Ȃ��̂������B ���`�Ȃ��̂Ƃ́A�Ⴆ�P�̃x�N�g����ϐ��Ƃ�������o�Ƃ����
��̃x�N�g����ϐ��Ƃ���i�O�C�P�j�e���\������`���ł���B ��̈�`����ϐ��Ƃ���i�P�C�O�j�e���\�����x�N�g���ł���B �����Ƃ́i�����̒l�j�A���L�̎��ɉ�����
 �̎��ł���B
�̎��ł���B
�Ⴆ�Έ�̃x�N�g����ϐ��Ƃ����`���� �Ƃ����
�Ƃ����
�@�@�@�@���@ �i
�i �j��
�j�� �i
�i
 �j��
�j��
 �i
�i �j��
�j��
 �@�@�i�����O�`�R�j�@
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j
�@�@�i�����O�`�R�j�@
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j
 �i
�i �j��
�j�� �̐����B
�̐����B
 �͂ǂ̌n�ł������l�ɂȂ�B(�U. �e���\�����̒藝���Q��)���ϐ��̐��`���ɂ�萬���̕ϊ����͕ۏ����B�ڍׂ��R. �e���\���̑㐔���Q��
�͂ǂ̌n�ł������l�ɂȂ�B(�U. �e���\�����̒藝���Q��)���ϐ��̐��`���ɂ�萬���̕ϊ����͕ۏ����B�ڍׂ��R. �e���\���̑㐔���Q��
�@�@�@���@�o�i �{
�{ �j���o�i
�j���o�i �j�{�o�i
�j�{�o�i �j�@�C�@�o�i��
�j�@�C�@�o�i�� �j���ɂo�i
�j���ɂo�i �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
�̓�̊W�����鎖�ł���B�Q�̃x�N�g����ϐ��Ƃ�������ɂ��Ă� �{
�{ �j���o�i
�j���o�i �j�{�o�i
�j�{�o�i �j�@�C�@�o�i��
�j�@�C�@�o�i�� �j���ɂo�i
�j���ɂo�i �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�j
�@�@�@���@���i�� �{��
�{�� ,
, 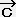 �j�������i
�j�������i ,
, 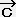 �j�{�����i
�j�{�����i ,
, 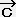 �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
�̊W�����藧���ł���B  �{��
�{�� ,
, 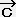 �j�������i
�j�������i ,
, 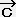 �j�{�����i
�j�{�����i ,
, 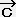 �j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
�j
�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�j
��̃x�N�g����ϐ��Ƃ���i�O�C�P�j�e���\������`���ł���B ��̈�`����ϐ��Ƃ���i�P�C�O�j�e���\�����x�N�g���ł���B �����Ƃ́i�����̒l�j�A���L�̎��ɉ�����

 �̎��ł���B
�̎��ł���B�Ⴆ�Έ�̃x�N�g����ϐ��Ƃ����`����
 �Ƃ����
�Ƃ���� �i
�i �j��
�j�� �i
�i
 �j��
�j��
 �i
�i �j��
�j��
 �@�@�i�����O�`�R�j�@
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j
�@�@�i�����O�`�R�j�@
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�R�j �i
�i �j��
�j�� �̐����B
�̐����B
 �͂ǂ̌n�ł������l�ɂȂ�B(�U. �e���\�����̒藝���Q��)���ϐ��̐��`���ɂ�萬���̕ϊ����͕ۏ����B�ڍׂ��R. �e���\���̑㐔���Q��
�͂ǂ̌n�ł������l�ɂȂ�B(�U. �e���\�����̒藝���Q��)���ϐ��̐��`���ɂ�萬���̕ϊ����͕ۏ����B�ڍׂ��R. �e���\���̑㐔���Q��
�Q. ���ρA���σe���\���ƓY���̈ʒu
�e���\���̐����ɉ����āA��t���̓Y���͂���炪���x�N�g���Ɣ��ɕϊ�����̂Łi�����̕ϊ��s�� 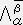 ��p���ĕϊ�����j���ρA���t���̓Y���͂���炪���x�N�g���Ɠ����ϊ��s��
��p���ĕϊ�����j���ρA���t���̓Y���͂���炪���x�N�g���Ɠ����ϊ��s�� 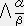 ��p���ĕϊ�����̂ŋ��ςƌĂ��B
�i�l�C�m�j�e���\���͂l�K���ςm�K���ςȃe���\���Ƃ�����B�i��t���̓Y���̐����l�A���t���̓Y���̐����m�j���A�P�� (�l�{�m) �K�e���\���ƌ����B�i�l�C�m�j�e���\���͕ϐ��Ƃ��Ăl�̈�`���Ƃm�̃x�N�g�������B�x�N�g����1�K���ςȃe���\���ŁA��`����1�K���ςȃe���\���ł���B
��p���ĕϊ�����̂ŋ��ςƌĂ��B
�i�l�C�m�j�e���\���͂l�K���ςm�K���ςȃe���\���Ƃ�����B�i��t���̓Y���̐����l�A���t���̓Y���̐����m�j���A�P�� (�l�{�m) �K�e���\���ƌ����B�i�l�C�m�j�e���\���͕ϐ��Ƃ��Ăl�̈�`���Ƃm�̃x�N�g�������B�x�N�g����1�K���ςȃe���\���ŁA��`����1�K���ςȃe���\���ł���B
�e���\���̐����̐������K�̃e���\���Ȃ�c���ɂȂ�B�c�͎������ŁA�O�������[�N���b�h��Ԃł͂c�͂R�ŁA�~���R�t�X�L�[�̎l��������ł͂c�͂S�ɂȂ�B�c���S�̎��A�Q�K�̃e���\���Ȃ�e���\���̐����̐��͂P�U�A�R�K�̃e���\���Ȃ�U�S�A�S�K�̃e���\���Ȃ�Q�T�U�ɂȂ�B
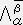 ��p���ĕϊ�����j���ρA���t���̓Y���͂���炪���x�N�g���Ɠ����ϊ��s��
��p���ĕϊ�����j���ρA���t���̓Y���͂���炪���x�N�g���Ɠ����ϊ��s�� 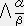 ��p���ĕϊ�����̂ŋ��ςƌĂ��B
�i�l�C�m�j�e���\���͂l�K���ςm�K���ςȃe���\���Ƃ�����B�i��t���̓Y���̐����l�A���t���̓Y���̐����m�j���A�P�� (�l�{�m) �K�e���\���ƌ����B�i�l�C�m�j�e���\���͕ϐ��Ƃ��Ăl�̈�`���Ƃm�̃x�N�g�������B�x�N�g����1�K���ςȃe���\���ŁA��`����1�K���ςȃe���\���ł���B
��p���ĕϊ�����̂ŋ��ςƌĂ��B
�i�l�C�m�j�e���\���͂l�K���ςm�K���ςȃe���\���Ƃ�����B�i��t���̓Y���̐����l�A���t���̓Y���̐����m�j���A�P�� (�l�{�m) �K�e���\���ƌ����B�i�l�C�m�j�e���\���͕ϐ��Ƃ��Ăl�̈�`���Ƃm�̃x�N�g�������B�x�N�g����1�K���ςȃe���\���ŁA��`����1�K���ςȃe���\���ł���B�e���\���̐����̐������K�̃e���\���Ȃ�c���ɂȂ�B�c�͎������ŁA�O�������[�N���b�h��Ԃł͂c�͂R�ŁA�~���R�t�X�L�[�̎l��������ł͂c�͂S�ɂȂ�B�c���S�̎��A�Q�K�̃e���\���Ȃ�e���\���̐����̐��͂P�U�A�R�K�̃e���\���Ȃ�U�S�A�S�K�̃e���\���Ȃ�Q�T�U�ɂȂ�B
3. �e���\���̑㐔
(1) �e���\���̐���
�i�l�C�m�j�e���\���̐����͂l�̓Y������ɁA�m�̓Y�������ɂ��B
�Ⴆ�q���i�P�C�P�j�e���\���Ƃ���ƁA�� �q�i �C
�C �j ��^���邽�߂ɁA��̌`��
�j ��^���邽�߂ɁA��̌`��  �ƈ�̃x�N�g��
�ƈ�̃x�N�g��  ��K�v�Ƃ���B
��K�v�Ƃ���B
����͐��� �q�i �C
�C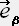 �j�� �q���� �����B
�j�� �q���� �����B
 ��
��  ��ϐ��ɂ��A�q�i
��ϐ��ɂ��A�q�i �C
�C �j �̒l��
�j �̒l��
�@�@�@���@�q�i �C
�C �j��
�q�i �o��
�j��
�q�i �o�� �C�`��
�C�`��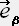 �j���o���`���q�i
�j���o���`���q�i  �C
�C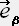 �j���o���`���q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�j
�j���o���`���q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�j
�Ⴆ�q���i�P�C�P�j�e���\���Ƃ���ƁA�� �q�i
 �C
�C �j ��^���邽�߂ɁA��̌`��
�j ��^���邽�߂ɁA��̌`��  �ƈ�̃x�N�g��
�ƈ�̃x�N�g��  ��K�v�Ƃ���B
��K�v�Ƃ���B����͐��� �q�i
 �C
�C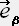 �j�� �q���� �����B
�j�� �q���� �����B ��
��  ��ϐ��ɂ��A�q�i
��ϐ��ɂ��A�q�i �C
�C �j �̒l��
�j �̒l���@�@�@���@�q�i
 �C
�C �j��
�q�i �o��
�j��
�q�i �o�� �C�`��
�C�`��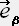 �j���o���`���q�i
�j���o���`���q�i  �C
�C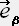 �j���o���`���q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�j
�j���o���`���q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�S�j
(2) �e���\���̐����̕ϊ�
�n�r����n �ւ̐����̕ϊ���
�ւ̐����̕ϊ���
�@�@�@���@�q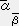 ���q�i
���q�i 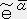 �C
�C �j���q�i
�j���q�i 
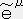 �C
�C
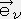 �j��
�j��
 �q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�T�j
�q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�T�j
�n ����n�r�ւ̐����̕ϊ���
����n�r�ւ̐����̕ϊ���
�@�@�@���@�q�������q�i �C
�C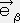 �j���q�i
�j���q�i 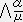
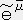 �C
�C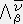
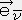 �j��
�j��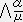
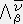 �q
�q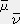 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�U�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�U�j
�������@�ŁA �n�r����n �ւ́i���C���j�e���\���̐����̕ϊ���
�ւ́i���C���j�e���\���̐����̕ϊ���
�@�@�@���@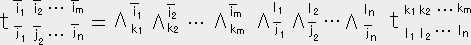 �@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
 �ւ̐����̕ϊ���
�ւ̐����̕ϊ����@�@�@���@�q
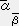 ���q�i
���q�i 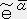 �C
�C �j���q�i
�j���q�i 
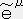 �C
�C
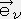 �j��
�j��
 �q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�T�j
�q����
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�T�j�n
 ����n�r�ւ̐����̕ϊ���
����n�r�ւ̐����̕ϊ����@�@�@���@�q�������q�i
 �C
�C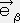 �j���q�i
�j���q�i 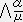
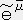 �C
�C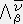
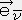 �j��
�j��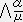
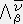 �q
�q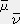 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�U�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�U�j�������@�ŁA �n�r����n
 �ւ́i���C���j�e���\���̐����̕ϊ���
�ւ́i���C���j�e���\���̐����̕ϊ���
�@�@�@���@
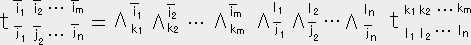 �@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�V�j
(3) �e���\���̊��
�x�N�g���A��`���������g���ĕ\�������l�ɁA�e���\���������g���ĕ\������B
��Ƃ��āi�P�C�Q�j�e���\�����l����B
1�K����2�K���ςȃe���\���̏W���̓x�N�g���̋�Ԃ����邩��A�C�ӂ̐��`�Ɨ��ȃe���\�������Ƃ��ėp���邱�Ƃ��o����B����� �Ƃ����
�Ƃ����
�@�@�@�s��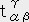

�@�@�@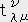 ��
�� 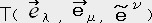 ��
�� 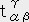

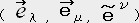
��̎��͎��̊W���Ӗ�����B
�@�@�@
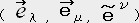 ��
�� 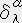
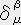
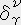
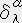 ��
��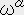 ��ł�
��ł� 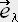 �̒l�ł���A
�̒l�ł���A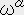 �i
�i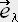 �j��
�j�� 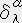
�@ �i�@6. �o�x�N�g���A�o��ԁ@(4) ��`���̊�����Q�Ɓj
���l�� 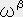 �i
�i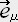 �j��
�j�� 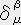 �@�@�@
�@�@�@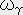 �i
�i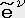 �j��
�j�� 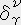
�]���� �͂��̒l�����傤�Ǔ�̑o�Ί��̒l�ƈ�̊��x�N�g���̒l�̐ςƂȂ�悤�ȃe���\���ł���A���ꂩ�玟�������_�����B
�͂��̒l�����傤�Ǔ�̑o�Ί��̒l�ƈ�̊��x�N�g���̒l�̐ςƂȂ�悤�ȃe���\���ł���A���ꂩ�玟�������_�����B
�@�@�@���@ ��
�� 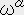

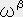

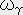 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
����ăe���\�� 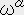

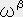

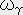 �͑S�Ă�1�K����2�K���ςȃe���\���ɂ���������ł���A�C�ӂ�1�K����2�K���ςȃe���\���͎��̗l�ɏ��������o����B
�͑S�Ă�1�K����2�K���ςȃe���\���ɂ���������ł���A�C�ӂ�1�K����2�K���ςȃe���\���͎��̗l�ɏ��������o����B
�@�@�@�s��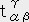
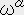

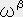

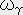 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
�n
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
�n �ł̂s��
�ł̂s��
�@�@�@�s��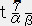
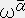

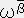

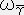 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
���̕ϊ���
�@�@�@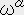 ��
��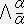
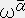 �@�C�@
�@�C�@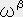 ��
��
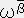 �@�C�@
�@�C�@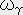 ��
��
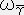 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
��̎����i�X�j�ɑ������ƁA�i�X�j��
�@�@�@�s��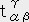
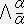
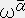


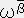


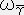 ��
�� 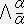


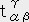
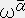

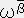

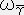
��̎��Ɓi�P�O�j���ׂ��
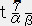 ��
�� 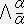


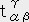
�ł��鎖��������B�����A�e���\���������g���ĕ\�����Ă��e���\���̐����̕ϊ���������B
�@�@�@�@�@�ik1,k2,�c,km=0�`3�@�@l1,l2,�c,ln=0�`3�j
1�K����2�K���ςȃe���\���̏W���̓x�N�g���̋�Ԃ����邩��A�C�ӂ̐��`�Ɨ��ȃe���\�������Ƃ��ėp���邱�Ƃ��o����B�����
 �Ƃ����
�Ƃ�����@�@�@�s��
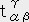

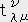 ��
�� 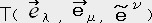 ��
�� 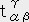

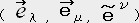
�@�@�@

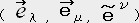 ��
�� 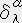
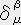
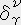
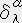 ��
��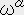 ��ł�
��ł� 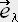 �̒l�ł���A
�̒l�ł���A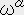 �i
�i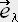 �j��
�j�� 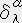
�@ �i�@6. �o�x�N�g���A�o��ԁ@(4) ��`���̊�����Q�Ɓj
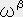 �i
�i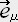 �j��
�j�� 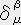 �@�@�@
�@�@�@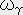 �i
�i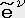 �j��
�j�� 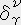
 �͂��̒l�����傤�Ǔ�̑o�Ί��̒l�ƈ�̊��x�N�g���̒l�̐ςƂȂ�悤�ȃe���\���ł���A���ꂩ�玟�������_�����B
�͂��̒l�����傤�Ǔ�̑o�Ί��̒l�ƈ�̊��x�N�g���̒l�̐ςƂȂ�悤�ȃe���\���ł���A���ꂩ�玟�������_�����B�@�@�@���@
 ��
�� 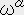

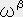

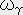 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�W�j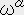

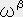

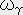 �͑S�Ă�1�K����2�K���ςȃe���\���ɂ���������ł���A�C�ӂ�1�K����2�K���ςȃe���\���͎��̗l�ɏ��������o����B
�͑S�Ă�1�K����2�K���ςȃe���\���ɂ���������ł���A�C�ӂ�1�K����2�K���ςȃe���\���͎��̗l�ɏ��������o����B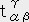
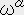

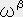

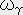 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�X�j
 �ł̂s��
�ł̂s��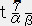
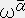

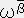

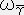 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�O�j
�@�@�@
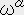 ��
��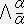
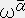 �@�C�@
�@�C�@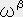 ��
��
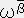 �@�C�@
�@�C�@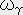 ��
��
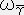 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�P�j
�@�@�@�s��
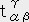
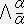
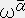


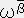


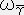 ��
�� 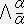


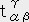
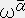

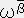

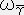
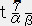 ��
�� 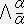


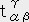
�ł��鎖��������B�����A�e���\���������g���ĕ\�����Ă��e���\���̐����̕ϊ���������B
���l�ȕ��@�����K�������K���ςȃe���\���������g���ĕ\�������
�@�@�@���@�s��
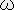 l1
l1
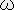 l2
l2 �c
�c
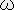 ln
ln

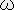 k1
k1
 k2
k2 �c
�c
 km
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
km
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�Q�j
�S. �e���\���̉��Z
�E ����A�������ϋy�ы��ς̊K���̓�������̃e���\���́A���ϋy�ы��ς̓Y���̑Ή���
�K���ɒ�߂�ƁA�e�����̘a�͏��߂̃e���\���Ɠ���̃e���\���ƂȂ�B
�E ��̃e���\���̐����̐ς��獂�K�̃e���\����������B�Ⴆ��
�@�@�@�s�������ʃ����u�������t�ʃ�
�K���ɒ�߂�ƁA�e�����̘a�͏��߂̃e���\���Ɠ���̃e���\���ƂȂ�B
�@�@�@�s�������ʃ����u�������t�ʃ�
�T. �e���\���̏k��
�e���\���̎��ɂ����āA�㉺�̓Y�������������Ă���ɂ��ĉ����鑀����e���\���̏k���Ƃ����B����ɂ��K�����Q����B��
�@�@���@�q�����ʃ����q�����@�C�@�`������ �s�ϗʁi�X�J���[�j�@�C�@�`���a�����s�ϗʁi�X�J���[�j
�@�@���@�s�����t�����v���@�i�x�N�g���j�@�@�C�@�@�s�����t�����o���@�i��`���j�@
�@�@���@�s�����t�����v���@�i�x�N�g���j�@�E�E�E�@�e���\���s�̓x�N�g���t����x�N�g���v�ւ̎ʑ���^����B
�@�@���@�s�����t�����o���@�i��`���j�@�@�E�E�E�@�e���\���s�͈�`���t�����`���o�ւ̎ʑ���^����B
�@�@���@�q�����ʃ����q�����@�C�@�`������ �s�ϗʁi�X�J���[�j�@�C�@�`���a�����s�ϗʁi�X�J���[�j
�@�@���@�s�����t�����v���@�i�x�N�g���j�@�@�C�@�@�s�����t�����o���@�i��`���j�@
�@�@���@�s�����t�����v���@�i�x�N�g���j�@�E�E�E�@�e���\���s�̓x�N�g���t����x�N�g���v�ւ̎ʑ���^����B
�@�@���@�s�����t�����o���@�i��`���j�@�@�E�E�E�@�e���\���s�͈�`���t�����`���o�ւ̎ʑ���^����B
�U. �e���\�����̒藝
��̃x�N�g���ƈ�̈�`����ϐ��Ƃ������T�Ƃ���B
T( ,
,  ,
,  ) �� T(
) �� T( 
 ,
, 
 ,
, 
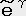 )
��
)
�� 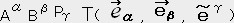
�@�@�@�i�@��,��,���@���@�O�`�R�@�j
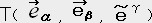 �͌nS�ɉ�����s�̐����Ł@
�͌nS�ɉ�����s�̐����Ł@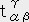 ��
�� 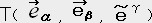 �@�Ƃ���
�@�Ƃ���
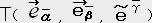 �͌n
�͌n �ɉ�����s�̐�����
�ɉ�����s�̐�����  ��
�� 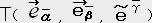 �@�Ƃ����B
�@�Ƃ����B
�@�@�@ ��
�� 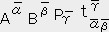 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�Ȃ�T�̓e���\���ł���Ƃ����̂��e���\�����̒藝�ł���B
�y�ؖ��z
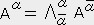 �@�@
�@�@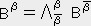 �@�@
�@�@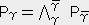 �@�ł��邩��A�������i�P�R�j�̎��̍��ӂɑ�����Đ��������
�@�ł��邩��A�������i�P�R�j�̎��̍��ӂɑ�����Đ��������
 ��
�� 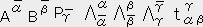 �@�@�ƂȂ�B
�@�@�ƂȂ�B
�i�P�R�j�̎��̉E�ӂƏ�̎��̉E�ӂ��
�@�@�@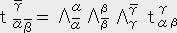
�����藧�B����̓e���\���̐����̕ϊ�����\���Ă���B�̂�T�̓e���\���ł���B
���̈Ӗ��́A�ǂ�ȍ��W�n��I��ł����̒l�������i���X�J���[�j�Ȃ�T�̓e���\���ł���Ƃ������ł���B
�t��T���e���\���Ȃ�i�P�R�j�����藧�B����T���e���\���Ȃ�ǂ�ȍ��W�n��I��ł����̒l�͓����ɂȂ�B
�y�ؖ��z�@�@ 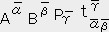 ��
�� 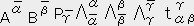 ��
�� 
T(
 ,
,  ,
,  ) �� T(
) �� T( 
 ,
, 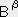
 ,
, 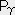
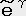 )
��
)
�� 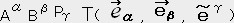
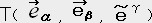 �͌nS�ɉ�����s�̐����Ł@
�͌nS�ɉ�����s�̐����Ł@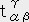 ��
�� 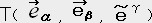 �@�Ƃ���
�@�Ƃ���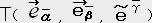 �͌n
�͌n �ɉ�����s�̐�����
�ɉ�����s�̐�����  ��
�� 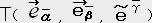 �@�Ƃ����B
�@�Ƃ����B
�@�@�@
 ��
�� 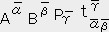 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�R�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�R�j
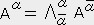 �@�@
�@�@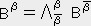 �@�@
�@�@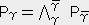 �@�ł��邩��A�������i�P�R�j�̎��̍��ӂɑ�����Đ��������
�@�ł��邩��A�������i�P�R�j�̎��̍��ӂɑ�����Đ�������� ��
�� 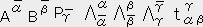 �@�@�ƂȂ�B
�@�@�ƂȂ�B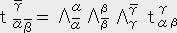
���̈Ӗ��́A�ǂ�ȍ��W�n��I��ł����̒l�������i���X�J���[�j�Ȃ�T�̓e���\���ł���Ƃ������ł���B
�t��T���e���\���Ȃ�i�P�R�j�����藧�B����T���e���\���Ȃ�ǂ�ȍ��W�n��I��ł����̒l�͓����ɂȂ�B
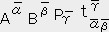 ��
�� 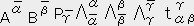 ��
�� 
�V. ���g���b�N
���g���b�N�͌v�ʃe���\�����͊�{�e���\���ƌĂ�A��{�x�N�g���i�����x�N�g���j�̃X�J���[�ς̑g�݂Œ�`�����Q�K�̃e���\���ł���B�i�e���\���ł��鎖�̏ؖ����P�O. �e���\���̗�@(3) �Q�K�̃e���\�����Q�Ɓj����
�y�n S �̊��x�N�g���̓��ρz
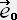 �E
�E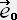 �� -1 ,�@
�� -1 ,�@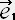 �E
�E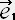 ��
�� 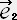 �E
�E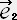 ��
�� 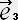 �E
�E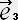 �� 1 ,�@
�� 1 ,�@ �E
�E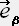 �� 0 �i �� �� �� �̎� �j
�y�n
�� 0 �i �� �� �� �̎� �j
�y�n  �̊��x�N�g���̓��ρz
�̊��x�N�g���̓��ρz
 �E
�E �� -1 ,�@
�� -1 ,�@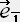 �E
�E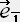 ��
�� 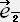 �E
�E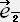 ��
�� 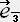 �E
�E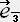 �� 1,�@
�� 1,�@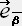 �E
�E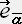 �� 0 �i
�� 0 �i 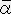 ��
��  �̎� �j
�]����g���b�N ������ ��
�̎� �j
�]����g���b�N ������ ��
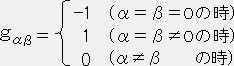
�~���R�t�X�L�[�̕��R�Ȏ���ł� ������ ����������� �Ə����B
�@�@�@���@ �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j
���g���b�N�͎����R�ł��邩�Ȃ����Ă��邩��\���B�����R�ȏꍇ�ɂ͏�L�̗l�ɊȒP�ł��邪�A��ʑ��Θ_�ň����Ȃ���������ł͕��G�Ȃ��̂ɂȂ�B
���g���b�N�͐��v�f�i���Ԋu�j��\�����ɗp������B����
�@�@�@���@����2���������������������@�@�i���C�����O�`�R�j �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j
�y�ؖ��z
�@�@�@�x�N�g�� ��
��  �� ����
�� ���� �Ƃ����
�Ƃ����  ��
��
�@�@�@ �̑S������� ��
�̑S������� �� ��
�@��
��
�@�� ��
��  ������ �� ������
������ �� ������
�@�@�@����2 ���b�� �b2 �� ��
�b2 �� �� �E��
�E�� ���i������
���i������ �j �E �i������
�j �E �i������ �j���i
�j���i �E
�E  �j������������
�j������������
�@�@�@�������� �E
�E  �@������
�@������
�@�@�@�@�@�@���@����2��������������������
�@�@�@���@�������� �E
�E  �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
���ꑊ�Θ_�ɉ�������x�N�g�����X�J���[���� �E
�E  �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�S�j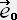 �E
�E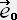 �� -1 ,�@
�� -1 ,�@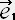 �E
�E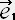 ��
�� 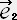 �E
�E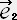 ��
�� 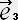 �E
�E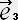 �� 1 ,�@
�� 1 ,�@ �E
�E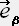 �� 0 �i �� �� �� �̎� �j
�� 0 �i �� �� �� �̎� �j
 �̊��x�N�g���̓��ρz
�̊��x�N�g���̓��ρz �E
�E �� -1 ,�@
�� -1 ,�@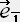 �E
�E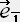 ��
�� 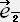 �E
�E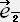 ��
�� 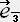 �E
�E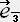 �� 1,�@
�� 1,�@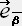 �E
�E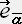 �� 0 �i
�� 0 �i 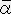 ��
��  �̎� �j
�̎� �j
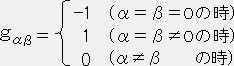
 �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�T�j���g���b�N�͐��v�f�i���Ԋu�j��\�����ɗp������B����
�@�@�@���@����2���������������������@�@�i���C�����O�`�R�j �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�U�j
�y�ؖ��z
�@�@�@�x�N�g��
 ��
��  �� ����
�� ���� �Ƃ����
�Ƃ����  ��
��
�@�@�@
 �̑S������� ��
�̑S������� �� ��
�@��
��
�@�� ��
��  ������ �� ������
������ �� ������
�@�@�@����2 ���b��
 �b2 �� ��
�b2 �� �� �E��
�E�� ���i������
���i������ �j �E �i������
�j �E �i������ �j���i
�j���i �E
�E  �j������������
�j�������������@�@�@��������
 �E
�E  �@������
�@�������@�@�@�@�@�@���@����2��������������������
�W. �i�O�C�Q�j�e���\��
�i�O�C�Q�j�e���\���͓�̃x�N�g����ϐ��Ƃ��Ă��e���\���ł���B���̗�Ƃ��ă��g���b�N�e���\�����̈�`���̐ςō��ꂽ�e���\����������B�i�O�C�Q�j�e���\���̑Ώ̐��A���Ώ̐�����d�v�Ȑ������������B
(1) �Ώ̐�
�� ���i�O�C�Q�j�e���\���Ƃ��A���̐����������� �����������i  ,
, 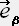 �j �Ƃ���B
�j �Ƃ���B
 ,
,  ��C�ӂ̃x�N�g���Ƃ������A��ʂɂ� ���i
��C�ӂ̃x�N�g���Ƃ������A��ʂɂ� ���i  ,
,  �j�� ���i
�j�� ���i  ,
,  �j �ł��邪
�j �ł��邪
�@�@�@�E�@���i  ,
,  �j�� ���i
�j�� ���i  ,
,  �j
�j
�̎��A�Ώ̂ƌĂ��B  ��
��  ��
��  ��
�� 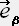 �Ƃ����ƁA����炩�琬���̊W���������B
�Ƃ����ƁA����炩�琬���̊W���������B
�@�@�@���@�������������� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�V�j
�C�ӂ́i�O�C�Q�j�e���\�������玟�̋K���ɂ��A�V�����Ώ̃e���\����(s)���`���鎖���o����B
�@�@�@�E�@��(s)�i ,
,  �j�� ���i
�j�� ���i  ,
,  �j�^�Q�{���i
�j�^�Q�{���i  ,
,  �j�^�Q
�j�^�Q
��(s)�͑Ώ̃e���\���ł���B���̐�����
�@�@�@���@��(����) �� �i�������{�������j�^�Q �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j
����͏d�v�Ȑ��w�I�����Ȃ̂œ��ʂȋL�@��p����B�i ��(����)�ƓY���Ɋ��ʂ�t���� �j
�� ��������W�n�őΏ̂Ȃ�ʂ̍��W�n�ł��Ώ̂ł���i�����̕ϊ���蓱�����j�B���Ώ̂Ȃ�ʂ̍��W�n�ł����Ώ̂ł���B
 ,
, 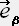 �j �Ƃ���B
�j �Ƃ���B ,
,  ��C�ӂ̃x�N�g���Ƃ������A��ʂɂ� ���i
��C�ӂ̃x�N�g���Ƃ������A��ʂɂ� ���i  ,
,  �j�� ���i
�j�� ���i  ,
,  �j �ł��邪
�j �ł��邪 ,
,  �j�� ���i
�j�� ���i  ,
,  �j
�j ��
��  ��
��  ��
�� 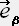 �Ƃ����ƁA����炩�琬���̊W���������B
�Ƃ����ƁA����炩�琬���̊W���������B�@�@�@���@�������������� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�V�j
�@�@�@�E�@��(s)�i
 ,
,  �j�� ���i
�j�� ���i  ,
,  �j�^�Q�{���i
�j�^�Q�{���i  ,
,  �j�^�Q
�j�^�Q �@�@�@���@��(����) �� �i�������{�������j�^�Q �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�W�j
(2) ���Ώ̐�
�@�@�@�E�@���i  ,
,  �j�� �[���i
�j�� �[���i  ,
,  �j�@�C�@�� ���� �� �[������
�j�@�C�@�� ���� �� �[������
�̎��A���Ώ̂ƌĂ��B
�C�ӂ́i�O�C�Q�j�e���\�� �� ���玟�̋K���ɂ��A�V�������Ώ̃e���\�� ��(�`) ���`���鎖���o����B
�@�@�@�E�@��(�`)�i ,
,  �j�� ���i
�j�� ���i  ,
,  �j�^�Q�[���i
�j�^�Q�[���i  ,
,  �j�^�Q
�j�^�Q
���̐�����
�@�@�@���@��[����] �� �i�������[�������j�^�Q �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�X�j
���̎������藧�B
�@�@�@���@������ �� �i�������{�������j�^�Q�{ �i�� �����[�������j�^�Q �� ��(����) �{ ��[����] �@�@�@�E�E�E�E�E�E�E�E�E�@�i�Q�O�j
�]���ĔC�ӂ́i�O�C�Q�j�e���\���́A�����Ώ̕����Ɣ��Ώ̕�������ӓI�ɕ����鎖���o����B
 ,
,  �j�� �[���i
�j�� �[���i  ,
,  �j�@�C�@�� ���� �� �[������
�j�@�C�@�� ���� �� �[�������@�@�@�E�@��(�`)�i
 ,
,  �j�� ���i
�j�� ���i  ,
,  �j�^�Q�[���i
�j�^�Q�[���i  ,
,  �j�^�Q
�j�^�Q �@�@�@���@��[����] �� �i�������[�������j�^�Q �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�P�X�j
���̎������藧�B
�@�@�@���@������ �� �i�������{�������j�^�Q�{ �i�� �����[�������j�^�Q �� ��(����) �{ ��[����] �@�@�@�E�E�E�E�E�E�E�E�E�@�i�Q�O�j
�X. �Y���̏グ�Ɖ���
�Y���̏グ�Ɖ����́A���̍��W�ϊ��A���̕ϊ��ł���B
(1) �x�N�g�������`���ւ̎ʑ��Ƃ��Ẵ��g���b�N
���g���b�N�̓x�N�g�������`���ւ̎ʑ��Ƃ��ē����B���̎��̈�`���̐��� P�� ��
�@�@�@���@P���� �i
�i �j��
�j��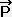 �E
�E ��P��
��P�� �E
�E  ���i
���i �E
�E  )P��
��������P��
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�P�j
)P��
��������P��
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�P�j
���g���b�N ������ �̓x�N�g���̐����̓Y���������A��`���̐����֕ϊ����铭��������B
�@�@�@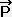 ���i���C���C���C��)�@�@�Ȃ��
�@�@
���i���C���C���C��)�@�@�Ȃ��
�@�@ ���i�|���C���C���C��)
���i�|���C���C���C��)
 �̐�����
�̐����� 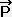 �̎��Ԑ����̕�����ς��鎖�ɂ���ċ��߂���B���̎��� ������ �̐����ɂ��B��ʑ��ΐ����_�ł́A�Y���̏グ�Ɖ����ɂ� ������ ���g���B
�̎��Ԑ����̕�����ς��鎖�ɂ���ċ��߂���B���̎��� ������ �̐����ɂ��B��ʑ��ΐ����_�ł́A�Y���̏グ�Ɖ����ɂ� ������ ���g���B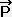 ��
��  �̑Ή��̋K�����܂���蕡�G�ɂȂ�B
�̑Ή��̋K�����܂���蕡�G�ɂȂ�B
���[�N���b�h��Ԃł̃f�J���g���W�ł̓��g���b�N�͒P�Ɂo��ij�p�ł���A��`���̐����Ƃ���ɑΉ�����x�N�g���̐����͓����ł���B
�@�@�@
�@�@�@���@P����
 �i
�i �j��
�j��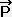 �E
�E ��P��
��P�� �E
�E  ���i
���i �E
�E  )P��
��������P��
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�P�j
)P��
��������P��
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�P�j�@�@�@
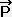 ���i���C���C���C��)�@�@�Ȃ��
�@�@
���i���C���C���C��)�@�@�Ȃ��
�@�@ ���i�|���C���C���C��)
���i�|���C���C���C��) �̐�����
�̐����� 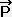 �̎��Ԑ����̕�����ς��鎖�ɂ���ċ��߂���B���̎��� ������ �̐����ɂ��B��ʑ��ΐ����_�ł́A�Y���̏グ�Ɖ����ɂ� ������ ���g���B
�̎��Ԑ����̕�����ς��鎖�ɂ���ċ��߂���B���̎��� ������ �̐����ɂ��B��ʑ��ΐ����_�ł́A�Y���̏グ�Ɖ����ɂ� ������ ���g���B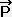 ��
��  �̑Ή��̋K�����܂���蕡�G�ɂȂ�B
�̑Ή��̋K�����܂���蕡�G�ɂȂ�B���[�N���b�h��Ԃł̃f�J���g���W�ł̓��g���b�N�͒P�Ɂo��ij�p�ł���A��`���̐����Ƃ���ɑΉ�����x�N�g���̐����͓����ł���B
(2)  ����
���� 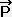 �ցF(1) �̋t�ϊ�
�ցF(1) �̋t�ϊ�
 ����
���� 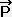 �ցF(1) �̋t�ϊ�
�ցF(1) �̋t�ϊ�
��`��  ����x�N�g��
����x�N�g�� 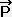 �ւ̎ʑ����������̋t�s����������p����B
�ւ̎ʑ����������̋t�s����������p����B
�@�@�@���@P����������P�� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j
�@�@�@
 ����x�N�g��
����x�N�g�� 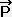 �ւ̎ʑ����������̋t�s����������p����B
�ւ̎ʑ����������̋t�s����������p����B�@�@�@���@P����������P�� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�Q�j
(3) ���g���b�N�̍�������
�����������ʃ����烁�g���b�N��"����"�������� ����������B����
�@�@�@�������� ���������ʃ�
�㎮�̉E�ӂ͂��݂��̋t�s��̐ς�����A����͒P�ʍs��ł���A�]���Ă���̓N���l�b�J�[�̃f���^�ł���B
�@�@�@���@���������������@�C�@ ���������S�@�@�ł��� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j
�@�@�@
�@�@�@�������� ���������ʃ�
�㎮�̉E�ӂ͂��݂��̋t�s��̐ς�����A����͒P�ʍs��ł���A�]���Ă���̓N���l�b�J�[�̃f���^�ł���B
�@�@�@���@���������������@�C�@ ���������S�@�@�ł��� �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�R�j
(4) �i�l�C�m�j�e���\�����i�l�|�P�C�m�{�P�j�e���\���Ɏʑ�
�s���������i�Q�C�P�j�e���\���Ƃ���B�Y�����������t���ɂ��āi�P�C�Q �j�e���\���Ƃ���B
�@�@�@���@�s�������������� �s������ �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�S�j
�@�@�@
�@�@�@���@�s�������������� �s������ �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�S�j
(5) �i�l�C�m�j�e���\�����i�l�{�P�C�m�|�P�j�e���\���Ɏʑ�
�s���������i�Q�C�P�j�e���\���Ƃ���B�Y�����ʂ���t���ɂ��āi�R�C�O �j�e���\���Ƃ���B
�@�@�@���@�s�����������ʃ� �s������ �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j
�@�@�@
�@�@�@���@�s�����������ʃ� �s������ �@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�@�i�Q�T�j
�P�O. �e���\���̗�
�e���\���̋�̓I�ȗ���K�����ɗ���B
(1) �O�K�̃e���\��
�X�J���[�͂O�K�̃e���\���ł���B���̂Ȃ���W�ϊ��Œl���ω����Ȃ�����B�Ⴆ�A���̑��x����� ���B
(2) �P�K�̃e���\��
�P�̃x�N�g����ϐ��Ƃ����`���̌n�r�ɉ����鐬���� �A�x�N�g���̐�����
�A�x�N�g���̐����� �Ƃ���ƌn�r�ɉ�������̒l��
�Ƃ���ƌn�r�ɉ�������̒l��

 �@�i�o�x�N�g���A�o������Q�Ɓj
���l�Ɍn
�@�i�o�x�N�g���A�o������Q�Ɓj
���l�Ɍn �ɉ�������̒l��
�ɉ�������̒l��

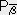 �@�@�@�@�i
�@�@�@�@�i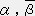 ���O�`�R�j
���O�`�R�j
 ��
��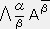 �ł��邩��@�i�x�N�g���̐����̕ϊ����Q�Ɓj
�ł��邩��@�i�x�N�g���̐����̕ϊ����Q�Ɓj
�@�@�@
 ��
�� 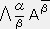
 ��
�� 
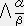

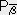 ��
��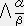
 �ł��邩��@�i��`���̐����̕ϊ����Q�Ɓj
�ł��邩��@�i��`���̐����̕ϊ����Q�Ɓj
�@�@�@
 ��
�� 
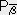 �@
�@
��L�̎��̓e���\���̒�`������B�̂Ɉ�`���͂P�K�̋��σe���\���ł���B
���l�ɂP�̈�`����ϐ��Ƃ���x�N�g�����P�K�̔��σe���\���ł���B
 �A�x�N�g���̐�����
�A�x�N�g���̐����� �Ƃ���ƌn�r�ɉ�������̒l��
�Ƃ���ƌn�r�ɉ�������̒l��
 �@�i�o�x�N�g���A�o������Q�Ɓj
���l�Ɍn
�@�i�o�x�N�g���A�o������Q�Ɓj
���l�Ɍn �ɉ�������̒l��
�ɉ�������̒l��
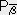 �@�@�@�@�i
�@�@�@�@�i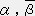 ���O�`�R�j
���O�`�R�j ��
��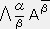 �ł��邩��@�i�x�N�g���̐����̕ϊ����Q�Ɓj
�ł��邩��@�i�x�N�g���̐����̕ϊ����Q�Ɓj
�@�@�@

 ��
�� 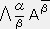
 ��
�� 
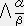

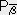 ��
��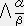
 �ł��邩��@�i��`���̐����̕ϊ����Q�Ɓj
�ł��邩��@�i��`���̐����̕ϊ����Q�Ɓj

 ��
�� 
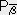 �@
�@
���l�ɂP�̈�`����ϐ��Ƃ���x�N�g�����P�K�̔��σe���\���ł���B
�@�@�@�o0 �� ���@,�@�o1 �� ��
 �i���ϐ��j�̐������@�@�@A0���� , �`1����
�i���ϐ��j�̐������@�@�@A0���� , �`1���� �����鐬����
�����鐬���� 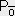 ��
��  �@,�@
�@,�@ ��
�� 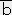 �@,�@
�@,�@ ��
�� 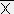 �@,�@
�@,�@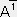 ��
��  �Ƃ����
�Ƃ����
 ��
�� 
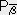 �� C �����藧�� �� �y�� �� �̓e���\���ł��鎖��������B
�� C �����藧�� �� �y�� �� �̓e���\���ł��鎖��������B�@�@�@

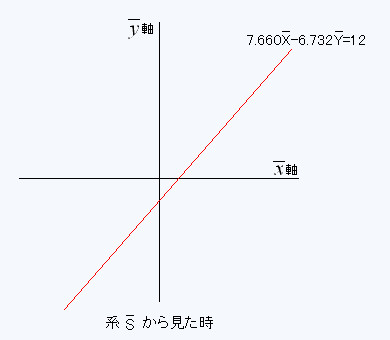
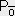 ��10cos��-2sin�Ɓ�7.660�@�@
��10cos��-2sin�Ɓ�7.660�@�@
 ��-10sin��-2cos�Ɓ�-6.732
��-10sin��-2cos�Ɓ�-6.732 ���猩�������̕������� 7.660
���猩�������̕������� 7.660 �[6.732
�[6.732 ��12�ƂȂ�B
��12�ƂȂ�B �͂��̏ꍇ���[�����c�ϊ��s��ł͂Ȃ������[�N���b�h��Ԃɉ����č��W�����v������������]�������̌n
�͂��̏ꍇ���[�����c�ϊ��s��ł͂Ȃ������[�N���b�h��Ԃɉ����č��W�����v������������]�������̌n ����n�r�ւ̕ϊ��s��ł���B
����n�r�ւ̕ϊ��s��ł���B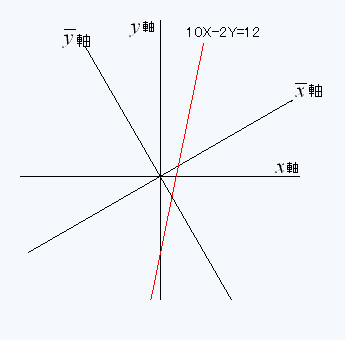
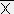 cos��-
cos��- sin�Ɓ@,�@����
sin�Ɓ@,�@����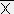 sin��+
sin��+ cos�� ��
cos�� �������{������C �̎��ɑ�����čs�����A�W�����e���\���Ȃ�W����ϊ���������������肵�����̌`���P��ŋ��܂�������ǂ��B���ɓ�K�ȏ�̍��K�̃e���\���ɉ����Ă̓e���\���̐���������ϊ�����悢����e���\���̗ǂ��������ɕ\���B
(3) �Q�K�̃e���\��
�Q�̃x�N�g���̐����`���A�a���̒��ϗʂ� ���������`���a���ƒ�`����� ������ �̓e���\���ł���B
�y�ؖ��z
�n �ɉ����鐬����
�ɉ����鐬����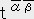 �A�x�N�g���̐�����
�A�x�N�g���̐�����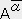 �A
�A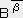 �Ƃ����
�Ƃ����
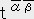 ��
�� 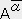
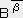 ��
�� 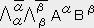 ��
�� 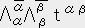
�̂� ������ �̓e���\���ł���B
 �ɉ����鐬����
�ɉ����鐬����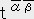 �A�x�N�g���̐�����
�A�x�N�g���̐�����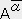 �A
�A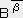 �Ƃ����
�Ƃ����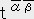 ��
�� 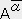
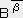 ��
�� 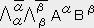 ��
�� 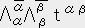
�̂� ������ �̓e���\���ł���B
���ꑊ�Θ_�ɉ�����~���R�t�X�L�[�̎l��������ł̓N���l�b�J�[�̃f���^�͉��L�̗l�ɂȂ�B
�@�@�@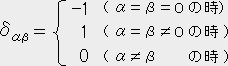
�y�ؖ��z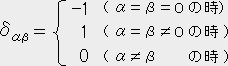
�n�r�ɉ�����N���l�b�J�[�̃f���^�̐����� �������@ �Q�̃x�N�g���̐������`���A�a���Ƃ����
�n�r�ɉ�������̒l�́@�`���a�� ��������-�`0�a0+�`1�a1+�`2�a2+�`3�a3
���l�Ɍn �ɉ�������̒l�́@
�ɉ�������̒l�́@
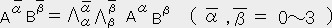 �@�ł���̂�
�@�ł���̂�
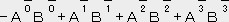 ��
�� 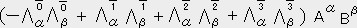
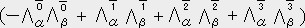 �@�̒l��
�@�̒l��
�@�@�@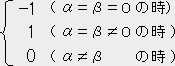 �@�@������
�@�@������
�]���ā@-�`0�a0+�`1�a1+�`2�a2+�`3�a3 ��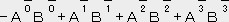
�n�r�A �ɉ�������̒l���������̂�
�ɉ�������̒l���������̂�
�̂ɃN���l�b�J�[�̃f���^�̓e���\���ł���B
�O�������[�N���b�h��Ԃɉ����Ă��ϊ��s��̒��𐫂ɂ��N���l�b�J�[�̃f���^�̓e���\���ł��鎖���ؖ��o����B
 �ɉ�������̒l�́@
�ɉ�������̒l�́@
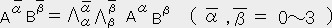 �@�ł���̂�
�@�ł���̂�
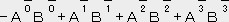 ��
�� 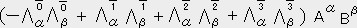
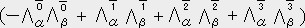 �@�̒l��
�@�̒l��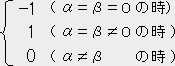 �@�@������
�@�@�������]���ā@-�`0�a0+�`1�a1+�`2�a2+�`3�a3 ��
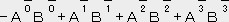
�n�r�A
 �ɉ�������̒l���������̂�
�ɉ�������̒l���������̂��O�������[�N���b�h��Ԃɉ����Ă��ϊ��s��̒��𐫂ɂ��N���l�b�J�[�̃f���^�̓e���\���ł��鎖���ؖ��o����B
��̃x�N�g��  ��
��  �̃X�J���[�ς�
�̃X�J���[�ς�
�@�@�@ �E
�E ��
�� 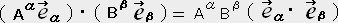
���g���b�N�e���\���̒�`��
�@�@�@������ ��  �E
�E �@�@�ł��邩��
�@�@�ł��邩��  �E
�E ��
�� 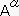
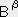 ������
������
�X�J���[�ς͌n�Ɉˑ����Ȃ�����@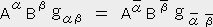
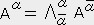 �@,�@
�@,�@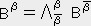 �@������
�@������

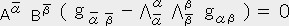
�x�N�g�� ��
��  �͔C�ӂ�����
�͔C�ӂ����� 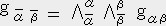
�̂Ƀ��g���b�N�̓e���\���ł���B
 ��
��  �̃X�J���[�ς�
�̃X�J���[�ς��@�@�@
 �E
�E ��
�� 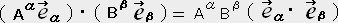
���g���b�N�e���\���̒�`��
 �E
�E �@�@�ł��邩��
�@�@�ł��邩��  �E
�E ��
�� 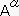
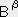 ������
������
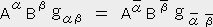
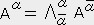 �@,�@
�@,�@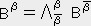 �@������
�@������
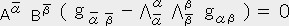
�x�N�g��
 ��
��  �͔C�ӂ�����
�͔C�ӂ����� 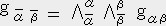
�Ȑ��͈�ʂ� �����Q�{�Q�������{�����Q�{�Q�����{�Q�������b �̌`�ŕ\�������B
�@�@�@�o00�����@,�@�o01�����@,�@�o02����
�@�@�@�o10�����@,�@�o11�����@,�@�o12����
�@�@�@�o20�����@,�@�o21�����@, �o22��0
�x�N�g�� �i���ϐ��j�@�̐����� A0���� , �`1���� , �`2��1 �Ƃ����
�i���ϐ��j�@�̐����� A0���� , �`1���� , �`2��1 �Ƃ����
�@�@�@�`���`���o�������b �ƂȂ�B�@�i��,����0�`2�j
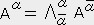 �@,�@
�@,�@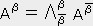 ������
������
�@�@�@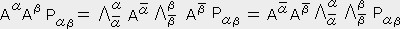
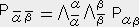 �ƕϊ������
�ƕϊ������
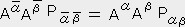 �� �b �ƂȂ�
�� �b �ƂȂ�
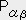 �܂� ���@,�@���@,�@���@,�@���@,�@�� �̓e���\���ƂȂ�B
�܂� ���@,�@���@,�@���@,�@���@,�@�� �̓e���\���ƂȂ�B
�y��z �Ȑ� 2���Q�{����-��
�Q-2���{����-1�̃O���t��`���B�@�@�@�o00�����@,�@�o01�����@,�@�o02����
�@�@�@�o10�����@,�@�o11�����@,�@�o12����
�@�@�@�o20�����@,�@�o21�����@, �o22��0
 �i���ϐ��j�@�̐����� A0���� , �`1���� , �`2��1 �Ƃ����
�i���ϐ��j�@�̐����� A0���� , �`1���� , �`2��1 �Ƃ����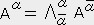 �@,�@
�@,�@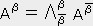 ������
������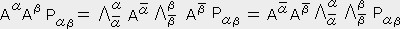
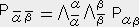 �ƕϊ������
�ƕϊ������
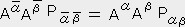 �� �b �ƂȂ�
�� �b �ƂȂ�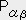 �܂� ���@,�@���@,�@���@,�@���@,�@�� �̓e���\���ƂȂ�B
�܂� ���@,�@���@,�@���@,�@���@,�@�� �̓e���\���ƂȂ�B
�@�@�@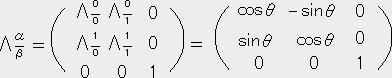
������/3�@�i���W�����v����60�K��]�j�Ƃ���B
 �@
�@
�@�@�@ 0.18�@,�@
0.18�@,�@ �[1.55�@,�@
�[1.55�@,�@ �[0.067
�[0.067
�@�@�@ 0.81�@,�@
0.81�@,�@ 1.12
1.12
�]���Čn ���猩���Ȑ��̕�������
���猩���Ȑ��̕�������
�@�@�@0.18 2-3.1
2-3.1
 +0.81
+0.81 2-0.134
2-0.134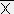 +2.24
+2.24 ��-1 �ƂȂ�B
��-1 �ƂȂ�B
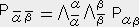 �@
�@
�@�@�@
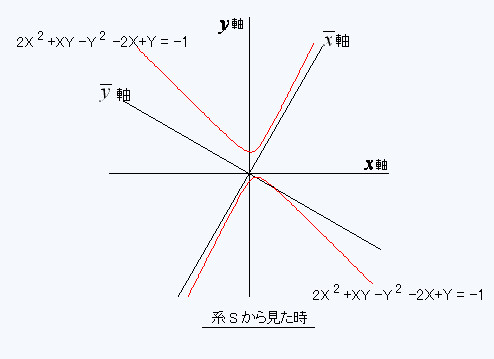
 0.18�@,�@
0.18�@,�@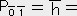 �[1.55�@,�@
�[1.55�@,�@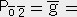 �[0.067
�[0.067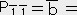 0.81�@,�@
0.81�@,�@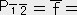 1.12
1.12 ���猩���Ȑ��̕�������
���猩���Ȑ��̕�������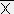 2-3.1
2-3.1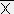
 +0.81
+0.81 2-0.134
2-0.134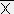 +2.24
+2.24 ��-1 �ƂȂ�B
��-1 �ƂȂ�B

�n�r�ɉ�����C�ӂ̐����s����l�����Ƃ����
�@�@�@�o�����l�����`���@�E�E�E�E�E�i�P�j�@�@�i �o�� �͈�`�� �̐����A�`���̓x�N�g��
�̐����A�`���̓x�N�g�� �̐��� �j
�̐��� �j
���l�Ɍn �ɉ�����
�ɉ�����
�@�@�@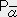 ��
��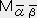
 �@�@�E�E�E�E�E�i�Q�j�@�@�Ƃ���
�@�@�E�E�E�E�E�i�Q�j�@�@�Ƃ���
�o����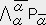 �@�C
�@�C 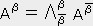 �@���i�P�j�ɑ�������
�@���i�P�j�ɑ�������
�@�@�@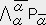 ��
�l����
��
�l���� 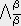
 ��
��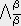 �l����
�l���� 
���ӂ� ���|�����
���|�����
�@�@�@
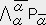 ��
��
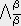 �l����
�l���� 

 ���P ������
���P ������
�@�@�@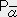 ��
��

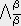 �l����
�l���� 
��̎��Ɓi�Q�j�̎����
�@�@�@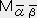 ��
��
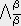 �l����
�l����
�����藧�B����̓e���\���̐����̕ϊ��������Ă���B
�̂ɐ����s��͂Q�K�̃e���\���ł���B
 �̐����A�`���̓x�N�g��
�̐����A�`���̓x�N�g�� �̐��� �j
�̐��� �j �ɉ�����
�ɉ�����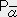 ��
��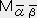
 �@�@�E�E�E�E�E�i�Q�j�@�@�Ƃ���
�@�@�E�E�E�E�E�i�Q�j�@�@�Ƃ����o����
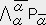 �@�C
�@�C 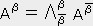 �@���i�P�j�ɑ�������
�@���i�P�j�ɑ��������@�@�@
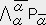 ��
�l����
��
�l���� 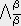
 ��
��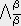 �l����
�l���� 
���ӂ�
 ���|�����
���|������@�@�@

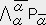 ��
��
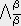 �l����
�l���� 

 ���P ������
���P �������@�@�@
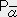 ��
��

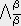 �l����
�l���� 
�@�@�@
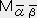 ��
��
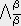 �l����
�l�����̂ɐ����s��͂Q�K�̃e���\���ł���B
(4) �R�K�ȏ�̃e���\��
�y�ؖ��z
���s�̌��z���s��
�@�@�@���s�� �@�@�E�E�E�E�E�i�P�j�ł���B�@�i�@
�@�@�E�E�E�E�E�i�P�j�ł���B�@�i�@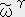 �@����`���̊���@�j
�@����`���̊���@�j
�s���P�K���ςP�K���ς̂Q�K�̃e���\���Ƃ���ƁA�s�����̗l�ɏ������Ƃ��o����B
�@�@�@�s�� �@�E�E�E�E�E�i�Q�j�@�@
�@�E�E�E�E�E�i�Q�j�@�@
�i�P�j�Ɓi�Q�j���i�Q�j�̌��z���s��
�@�@�@���s��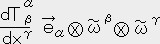 ��
��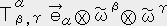
�@�@�@�@�@�i�@�s�����C���ɂ��Ă��@������\���L�@�@���Q�Ɓ@�j
�̂Ɍ��z���s�͂R�K�̃e���\���ł���B���l�ȕ��@�łS�K�̃e���\����肾�������o����B
�����ł͊��x�N�g���y�ъ���`���͎���Ƃ���ň��Ƃ����������g���Ă���B��ʑ��Θ_�̋Ȃ�����Ԃł͂��̎��͉���o���Ȃ��B
�@�@�@���s��
 �@�@�E�E�E�E�E�i�P�j�ł���B�@�i�@
�@�@�E�E�E�E�E�i�P�j�ł���B�@�i�@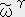 �@����`���̊���@�j
�@����`���̊���@�j�@�@�@�s��
 �@�E�E�E�E�E�i�Q�j�@�@
�@�E�E�E�E�E�i�Q�j�@�@�@�@�@���s��
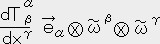 ��
��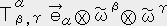
�����ł͊��x�N�g���y�ъ���`���͎���Ƃ���ň��Ƃ����������g���Ă���B��ʑ��Θ_�̋Ȃ�����Ԃł͂��̎��͉���o���Ȃ��B
�t�^�P�F�Ώ̃e���\���̌ŗL�l
��̃e���\�� �sij �̓x�N�g�����P���ʑ����߂�B�i i,j=1�`3 �j �����@�ui���sij�tj�@���[�N���b�h��Ԃł̃f�J���g���W�ł͈�`���̐����Ƃ���ɑΉ�����x�N�g���̐����͓����ł���̂ŁA�ui���ui �ł���B���@�ui���ɂti�@�����@�sij �tj �� �ɂti�@�Ƃ��A�����W�J�����
�@�@�@�i�s11�[�Ɂj�t1�{�s12�t2�@�@�@�@�@�@�{�s13�t3�@�@�@�@�@���@�O
�@�@�@�s21�t1�@�@�@�@�{�i�s22�[�Ɂj�t2�@�@�{�s23�t3�@�@�@�@�@���@�O
�@�@�@�s31�t1�@�@�@�@�{�s32�t2�@�@�@�@�@�@�{�i�s33�[�Ɂj�t3�@���@�O
��̐Ď��ꎟ�������ɉ����� �ti ���O�ȊO�̉��������߂ɂ͉��L�̍s�̒l���O�ł��鎖���K�v�ł���B
�@�@ �@�@�@�@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�@�@�@�@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
��̕��������e���\�� �sij ���ŗL�������Ƃ����A���̍����ŗL�l�Ƃ����A�ŗL�l�ɂɑΉ�����x�N�g�� �ti ���ŗL�x�N�g���Ƃ����B�ŗL�x�N�g���������s���ł���B
�y�e���\���Ȗʁz
�@�@�@�i�s11�[�Ɂj�t1�{�s12�t2�@�@�@�@�@�@�{�s13�t3�@�@�@�@�@���@�O
�@�@�@�s21�t1�@�@�@�@�{�i�s22�[�Ɂj�t2�@�@�{�s23�t3�@�@�@�@�@���@�O
�@�@�@�s31�t1�@�@�@�@�{�s32�t2�@�@�@�@�@�@�{�i�s33�[�Ɂj�t3�@���@�O
��̐Ď��ꎟ�������ɉ����� �ti ���O�ȊO�̉��������߂ɂ͉��L�̍s�̒l���O�ł��鎖���K�v�ł���B
�@�@
 �@�@�@�@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�@�@�@�@�@ �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j��̕��������e���\�� �sij ���ŗL�������Ƃ����A���̍����ŗL�l�Ƃ����A�ŗL�l�ɂɑΉ�����x�N�g�� �ti ���ŗL�x�N�g���Ƃ����B�ŗL�x�N�g���������s���ł���B
�y�e���\���Ȗʁz
���s���W�n�őΏ̂ȃe���\�� �sij �ɑ��āA���_�𒆐S�Ƃ���Q���Ȗ�
�@�@�@�sij ��i ��j �� �P�@�@�@�i ��1�������A��2�������A��3������ �j �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
���e���\���Ȗ��Ƃ����B�sij ���ŗL�l����1,��2,��3 �Ȃ�A�����ɑ����ŗL�x�N�g���͒�������̂ŁA�P�ʉ������ŗL�x�N�g�������x�N�g���Ƃ����V�������W�n�̂��ƂŁA��L�̓Ȗʂ�
�@�@�@��1�i��1�j2�{��2�i��2�j2�{��3�i��3�j2�@���@�P �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�ƂȂ�B�����e���\�� �sij �̌ŗL�x�N�g���̓e���\���Ȗʂ̎厲���߂�B
�i ���i���j�̏ؖ� �j
�@�@�@�sij ��i ��j �� �P�@�@�@�i ��1�������A��2�������A��3������ �j �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
���e���\���Ȗ��Ƃ����B�sij ���ŗL�l����1,��2,��3 �Ȃ�A�����ɑ����ŗL�x�N�g���͒�������̂ŁA�P�ʉ������ŗL�x�N�g�������x�N�g���Ƃ����V�������W�n�̂��ƂŁA��L�̓Ȗʂ�
�@�@�@��1�i��1�j2�{��2�i��2�j2�{��3�i��3�j2�@���@�P �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�ƂȂ�B�����e���\�� �sij �̌ŗL�x�N�g���̓e���\���Ȗʂ̎厲���߂�B
�i ���i���j�̏ؖ� �j
�sij �̌ŗL�l�y�ьŗL�x�N�g�����A�sij �͑Ίp���o����B�i�Ȃ���������@�t�^�P�F�����s��̑Ίp�s��ւ̕ϊ����Q�Ɓj�@�Ίp�����������s���i�����W�ϊ��s��j�� �� �Ƃ����
�@�@�@�si j �� ��ii ��jj �sij�@�C�@�si j �� �@�@��1�C��2�C��3 �͌ŗL�l�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�@�@��1�C��2�C��3 �͌ŗL�l�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
��i �� ��ii ��i�@�C�@��j �� ��jj ��j �����i���j�̍��ӂɑ������Ɓ@��ii ��jj �sij ��i ��j �� �P
���̎��Ǝ��i���j��莮�i���j�����藧�B �s��ŕ\������ƁA���i���j�� �i ��1�@��2�@��3 �j �s �� �P
�� �P
�i ��1�@��2�@��3 �j �� ��t �i ��1�@��2�@��3 �j�@�C�@ �� ��
�� ��  �@����̎��ɑ������
��t�s�� ��
�@����̎��ɑ������
��t�s�� ��  �@�Ƃ�莮�i���j�����藧�B
�@�Ƃ�莮�i���j�����藧�B
�i���j�@�@�@�si j �� ��ii ��jj �sij�@�C�@�si j ��
 �@�@��1�C��2�C��3 �͌ŗL�l�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j
�@�@��1�C��2�C��3 �͌ŗL�l�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�@�i���j��i �� ��ii ��i�@�C�@��j �� ��jj ��j �����i���j�̍��ӂɑ������Ɓ@��ii ��jj �sij ��i ��j �� �P
���̎��Ǝ��i���j��莮�i���j�����藧�B �s��ŕ\������ƁA���i���j�� �i ��1�@��2�@��3 �j �s
 �� �P
�� �P
�i ��1�@��2�@��3 �j �� ��t �i ��1�@��2�@��3 �j�@�C�@
 �� ��
�� ��  �@����̎��ɑ������
��t�s�� ��
�@����̎��ɑ������
��t�s�� ��  �@�Ƃ�莮�i���j�����藧�B
�@�Ƃ�莮�i���j�����藧�B
�e���\�� �sij �����L�Ƃ���B
�@�@�@�sij�@���@
�ŗL�������i��L�Q�Ɓj�������ŗL�l�����߂�ƁA�ŗL�l�� �W�A�T�A�R �ƂȂ�B�ŗL�l�W�ɑ����ŗL�x�N�g���̐������w�C�x�C�y�Ƃ����
�@�@�@
 ���W
���W �@
�@ �@�w���w�C�@�x���w�C�@�y���|�w
�@�w���w�C�@�x���w�C�@�y���|�w
�]���ČŗL�l�W�ɑΉ�����P�ʉ������ŗL�x�N�g���́@
���l�ɌŗL�l�T�ɑΉ�����P�ʉ������ŗL�x�N�g���́@
���l�ɌŗL�l�R�ɑΉ�����P�ʉ������ŗL�x�N�g���́@
�̂������s������
�@�@�@�� ��
�����s��ɂ��Ίp�����ꂽ �s ��
�@�@�@��t�s�� ��
�P�ʉ������ŗL�x�N�g�������x�N�g���Ƃ����V�������W�n�̂��Ƃł̃e���\���Ȗʂ͎��i���j���
�@�@�@�W�i��1�j2�{�T�i��2�j2�{�R�i��3�j2�@���@�P
�ƂȂ�B����͉��}�̗l�ȑȉ~�ʂƂȂ�B
�@�@�@
�@�@�@�sij�@���@

�ŗL�������i��L�Q�Ɓj�������ŗL�l�����߂�ƁA�ŗL�l�� �W�A�T�A�R �ƂȂ�B�ŗL�l�W�ɑ����ŗL�x�N�g���̐������w�C�x�C�y�Ƃ����
�@�@�@

 ���W
���W �@
�@ �@�w���w�C�@�x���w�C�@�y���|�w
�@�w���w�C�@�x���w�C�@�y���|�w�]���ČŗL�l�W�ɑΉ�����P�ʉ������ŗL�x�N�g���́@

���l�ɌŗL�l�T�ɑΉ�����P�ʉ������ŗL�x�N�g���́@

���l�ɌŗL�l�R�ɑΉ�����P�ʉ������ŗL�x�N�g���́@

�̂������s������
�@�@�@�� ��

�����s��ɂ��Ίp�����ꂽ �s ��
�@�@�@��t�s�� ��

�P�ʉ������ŗL�x�N�g�������x�N�g���Ƃ����V�������W�n�̂��Ƃł̃e���\���Ȗʂ͎��i���j���
�@�@�@�W�i��1�j2�{�T�i��2�j2�{�R�i��3�j2�@���@�P
�ƂȂ�B����͉��}�̗l�ȑȉ~�ʂƂȂ�B
�@�@�@

�t�^�Q�F�������[�����g
�������[�����g�i�������\���j�͊p�^���ʂ��v�Z����ߒ��œ��o�����B���̂����_�n�̉��ɉ�]���鎞�A����u�Ԃɉ�����p���x�� �� �i�ȉ������ŕ\���������̓x�N�g�����͈�`����\���j�Ƃ��鎞�A���̂̓_�o�i�n�o�����j�̑��x �� �́A������x�� �ix�̓x�N�g���̊O�ςł���j�ƂȂ�B��i �����_�A���̂̊p�^���ʂ� �k �Ƃ����
�@�@�@�k �� ��ix�i��i��i�j ��
��ix�i��i��i�j ��  ��i��ix�i��x��i�j ��
��i��ix�i��x��i�j ��  ��i�o���i��2i�j�[��i�i����i�j�p
��i�o���i��2i�j�[��i�i����i�j�p
�ƂȂ�A���� �� ������
�@�@�@�kx �� ��i�o��x�i��2i�{��2i�{��2i�j�[��i�i��x��i�{��y��i�{��z��i�j�p
��i�o��x�i��2i�{��2i�{��2i�j�[��i�i��x��i�{��y��i�{��z��i�j�p
�@�@�@�@ �� ��x ��i�i��2i�{��2i�j�[��y
��i�i��2i�{��2i�j�[��y  ��i��i��i�[��z
��i��i��i�[��z  ��i��i��i��i
��i��i��i��i
�ƂȂ�B������
�@�@�@���@�hxx�� ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u
�@�@�@���@�hyy�� ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u
�@�@�@���@�hzz�� ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u
�@�@�@���@�hyz�� �hzy�� �[ ��i��i��i���[�������u
��i��i��i���[�������u
�@�@�@���@�hzx�� �hxz�� �[ ��i��i��i���[�������u
��i��i��i���[�������u
�@�@�@���@�hxy�� �hyx�� �[ ��i��i��i���[�������u
��i��i��i���[�������u
�@�@�@�@�@�@���͖��x�A���u���������������ł���B�ϕ��L�����͈���������Ă��邪�A�{���͎O�K�v�ł���B
�ƒ�`������ʂ�����ƁA�p�^���� �k �����A���A�� ���� �kx �A �ky �A �kz ��
�@�@�@�kx���hxx��x�{�hxy��y�{�hxz��z�@�C�@�ky���hyx��x�{�hyy��y�{�hyz��z�@�C�@�kz���hzx��x�{�hzy��y�{�hzz��z
�Ə�����B�hxx�A�hyy�A�hzz�����ꂼ�����A���A�����Ɋւ��鍄�̂��������[�����g�Ƃ����A�[�hyz�A�|�hzx�A�|�hxy����������Ƃ����B����������̂̌`�A���ʂ̕��z��ԁA��]���̈ʒu���ɂ���Ē�܂�萔�ł���B��̎����番����l�ɁA�������[�����g�͈�̎����畨�̂��\������e���_�܂ł̋������̓��Ǝ������Ƃ̐ς̑��a�ł���B
�������[�����g�͓�K�̑Ώ̂ȃe���\���ł��邩��A���܂��������W�n��I�ׂC�Ίp���o����i�t�^�P�F�Ώ̃e���\���̌ŗL�l���� �Ȃ�������̕t�^�P ���Q�Ɓj�B���̎��o�Ă���Ίp�����ꂽ�������[�����g���劵�����[�����g�ƌĂсA���ꂪ���藧���W�n�������厲�Ƃ����B�����Ď厲�Ɋւ�����������͑S�ĂO�ɂȂ�B
�@�@�@�k ��
 ��ix�i��i��i�j ��
��ix�i��i��i�j ��  ��i��ix�i��x��i�j ��
��i��ix�i��x��i�j ��  ��i�o���i��2i�j�[��i�i����i�j�p
��i�o���i��2i�j�[��i�i����i�j�p�ƂȂ�A���� �� ������
�@�@�@�kx ��
 ��i�o��x�i��2i�{��2i�{��2i�j�[��i�i��x��i�{��y��i�{��z��i�j�p
��i�o��x�i��2i�{��2i�{��2i�j�[��i�i��x��i�{��y��i�{��z��i�j�p�@�@�@�@ �� ��x
 ��i�i��2i�{��2i�j�[��y
��i�i��2i�{��2i�j�[��y  ��i��i��i�[��z
��i��i��i�[��z  ��i��i��i��i
��i��i��i��i�ƂȂ�B������
�@�@�@���@�hxx��
 ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u�@�@�@���@�hyy��
 ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u�@�@�@���@�hzz��
 ��i�i��2i�{��2i�j�������i��2�{��2�j���u
��i�i��2i�{��2i�j�������i��2�{��2�j���u�@�@�@���@�hyz�� �hzy�� �[
 ��i��i��i���[�������u
��i��i��i���[�������u�@�@�@���@�hzx�� �hxz�� �[
 ��i��i��i���[�������u
��i��i��i���[�������u�@�@�@���@�hxy�� �hyx�� �[
 ��i��i��i���[�������u
��i��i��i���[���ς������u�@�@�@�@�@�@���͖��x�A���u���������������ł���B�ϕ��L�����͈���������Ă��邪�A�{���͎O�K�v�ł���B
�ƒ�`������ʂ�����ƁA�p�^���� �k �����A���A�� ���� �kx �A �ky �A �kz ��
�@�@�@�kx���hxx��x�{�hxy��y�{�hxz��z�@�C�@�ky���hyx��x�{�hyy��y�{�hyz��z�@�C�@�kz���hzx��x�{�hzy��y�{�hzz��z
�Ə�����B�hxx�A�hyy�A�hzz�����ꂼ�����A���A�����Ɋւ��鍄�̂��������[�����g�Ƃ����A�[�hyz�A�|�hzx�A�|�hxy����������Ƃ����B����������̂̌`�A���ʂ̕��z��ԁA��]���̈ʒu���ɂ���Ē�܂�萔�ł���B��̎����番����l�ɁA�������[�����g�͈�̎����畨�̂��\������e���_�܂ł̋������̓��Ǝ������Ƃ̐ς̑��a�ł���B
�������[�����g�͓�K�̑Ώ̂ȃe���\���ł��邩��A���܂��������W�n��I�ׂC�Ίp���o����i�t�^�P�F�Ώ̃e���\���̌ŗL�l���� �Ȃ�������̕t�^�P ���Q�Ɓj�B���̎��o�Ă���Ίp�����ꂽ�������[�����g���劵�����[�����g�ƌĂсA���ꂪ���藧���W�n�������厲�Ƃ����B�����Ď厲�Ɋւ�����������͑S�ĂO�ɂȂ�B
�t�^�R�F�����w�ɉ�����e���\��
(1) ���̓e���\��
(2) �����e���\��
���̂ɘc�݂������鈳�̓e���\���͂Q�̃x�N�g����ϐ��Ƃ���i�O�C�Q�j�̂Q�K���ςȃe���\���ł���B
���̓e���\����T�AT�̐������sij�A�ϐ��̃x�N�g���� �A
�A �Ƃ���B
�Ƃ���B �A
�A �����̓��̂P�_�ɉ�����C�ӂ̖ʂɑ���P�ʖ@���x�N�g���ł���B
�����̓��̂P�_�ɉ�����C�ӂ̖ʂɑ���P�ʖ@���x�N�g���ł���B
�@�@�@�sij �� T( i �C
i �C j )�@�@�C�@
j )�@�@�C�@ �� �i ��1�C��2�C��3 �j�@�@�C�@
�� �i ��1�C��2�C��3 �j�@�@�C�@ �� �i ��1�C��2�C��3 �j
�� �i ��1�C��2�C��3 �j
�@�@�@�@�@�@�@�@�@�i���C�����P�`�R�@�P�F�����@�Q�F�����@�R�F�����j
�@�@�@T( �C
�C ) �� T( ��i
) �� T( ��i  i �C��j
i �C��j  j ) �� ��i ��j T (
j ) �� ��i ��j T (  i �C
i �C j ) �� �sij ��i ��j
j ) �� �sij ��i ��j
�sij ��}�Ŏ�����

��P�̓Y���͖ʂ�\���B�ʂ͍��W���ɑ��Đ����ɂȂ�l�ȖʂŒ�`�����B��Q�̓Y���͈��͂̕�����\���B�Ⴆ�sxy�͂w���ɐ����Ȗʂɑ��Ăx�����̈��͂�\���B�sxy�Ƃsyx�͓������B���̂Ȃ�sxy�͂y���̉��ɂx�����ɉ�]������͂ƂȂ�A�syx�͂y���̉��ɂw�����ɉ�]������͂ƂȂ�B���������͉̂�]���Ă��Ȃ��̂łsxy���syx�ł���B��ʂɂsij ���sji�ł���B�]���Ăs�͑Ώ̂ȃe���\���ł���B
�sij �̂P�s�ڂ����ʂł̈��͂̃x�N�g���̐�����\���A����ƃx�N�g�� �Ƃ̓��ς��Ƃ�A���ʂ�
�Ƃ̓��ς��Ƃ�A���ʂ� �����̈��͂̐��� �ox ���v�Z����B�oy�A�oz �����l�ł���B���ŏ����Ɖ��L�̗l�ɂȂ�B
�����̈��͂̐��� �ox ���v�Z����B�oy�A�oz �����l�ł���B���ŏ����Ɖ��L�̗l�ɂȂ�B
�@�@�@ �@�@�C�@Pi �� �sij��j
�@�@�C�@Pi �� �sij��j
����Pi �𐬕��Ƃ���x�N�g���ƃx�N�g�� �Ƃ̓��ς��Ƃ�A
�Ƃ̓��ς��Ƃ�A �����̑S���� �o ���v�Z����B�ʏ�A�x�N�g��
�����̑S���� �o ���v�Z����B�ʏ�A�x�N�g��  ��
��  �͓����x�N�g�����w�肷��B����
�͓����x�N�g�����w�肷��B����  �����ւ̈��� �o ��
�����ւ̈��� �o ��
�@�@�@�o = �oi��i �� �sij�� i��j
��̎����s��̌`�ŕ\���ƁA�@��tT���@�@�i ��t�����̓]�u��\���B�j
��t���i�P�^ �C�P�^
�C�P�^ �C�O�j �Ƃ���ƁA
�C�O�j �Ƃ���ƁA  �����ւ̈��͂͏�̎���� �sxx�^�Q�{�sxy�{�syy�^�Q �ƂȂ�B
�����ւ̈��͂͏�̎���� �sxx�^�Q�{�sxy�{�syy�^�Q �ƂȂ�B
�i �s ���e���\���ł��鎖�̏ؖ� �j
���̓e���\����T�AT�̐������sij�A�ϐ��̃x�N�g����
 �A
�A �Ƃ���B
�Ƃ���B �A
�A �����̓��̂P�_�ɉ�����C�ӂ̖ʂɑ���P�ʖ@���x�N�g���ł���B
�����̓��̂P�_�ɉ�����C�ӂ̖ʂɑ���P�ʖ@���x�N�g���ł���B�@�@�@�sij �� T(
 i �C
i �C j )�@�@�C�@
j )�@�@�C�@ �� �i ��1�C��2�C��3 �j�@�@�C�@
�� �i ��1�C��2�C��3 �j�@�@�C�@ �� �i ��1�C��2�C��3 �j
�� �i ��1�C��2�C��3 �j�@�@�@�@�@�@�@�@�@�i���C�����P�`�R�@�P�F�����@�Q�F�����@�R�F�����j
�@�@�@T(
 �C
�C ) �� T( ��i
) �� T( ��i  i �C��j
i �C��j  j ) �� ��i ��j T (
j ) �� ��i ��j T (  i �C
i �C j ) �� �sij ��i ��j
j ) �� �sij ��i ��j�sij ��}�Ŏ�����

��P�̓Y���͖ʂ�\���B�ʂ͍��W���ɑ��Đ����ɂȂ�l�ȖʂŒ�`�����B��Q�̓Y���͈��͂̕�����\���B�Ⴆ�sxy�͂w���ɐ����Ȗʂɑ��Ăx�����̈��͂�\���B�sxy�Ƃsyx�͓������B���̂Ȃ�sxy�͂y���̉��ɂx�����ɉ�]������͂ƂȂ�A�syx�͂y���̉��ɂw�����ɉ�]������͂ƂȂ�B���������͉̂�]���Ă��Ȃ��̂łsxy���syx�ł���B��ʂɂsij ���sji�ł���B�]���Ăs�͑Ώ̂ȃe���\���ł���B
�sij �̂P�s�ڂ����ʂł̈��͂̃x�N�g���̐�����\���A����ƃx�N�g��
 �Ƃ̓��ς��Ƃ�A���ʂ�
�Ƃ̓��ς��Ƃ�A���ʂ� �����̈��͂̐��� �ox ���v�Z����B�oy�A�oz �����l�ł���B���ŏ����Ɖ��L�̗l�ɂȂ�B
�����̈��͂̐��� �ox ���v�Z����B�oy�A�oz �����l�ł���B���ŏ����Ɖ��L�̗l�ɂȂ�B�@�@�@
 �@�@�C�@Pi �� �sij��j
�@�@�C�@Pi �� �sij��j����Pi �𐬕��Ƃ���x�N�g���ƃx�N�g��
 �Ƃ̓��ς��Ƃ�A
�Ƃ̓��ς��Ƃ�A �����̑S���� �o ���v�Z����B�ʏ�A�x�N�g��
�����̑S���� �o ���v�Z����B�ʏ�A�x�N�g��  ��
��  �͓����x�N�g�����w�肷��B����
�͓����x�N�g�����w�肷��B����  �����ւ̈��� �o ��
�����ւ̈��� �o ���@�@�@�o = �oi��i �� �sij�� i��j
��̎����s��̌`�ŕ\���ƁA�@��tT���@�@�i ��t�����̓]�u��\���B�j
��t���i�P�^
 �C�P�^
�C�P�^ �C�O�j �Ƃ���ƁA
�C�O�j �Ƃ���ƁA  �����ւ̈��͂͏�̎���� �sxx�^�Q�{�sxy�{�syy�^�Q �ƂȂ�B
�����ւ̈��͂͏�̎���� �sxx�^�Q�{�sxy�{�syy�^�Q �ƂȂ�B
�n�n�ł̈��͂� �sij��i��j �ŁA�n�n�ł̈��͂� �si j ��i��j �ł���B
���͂͌n�n�ł��n�n�ł�����������@�sij�� i��j �� �si j ��i��j
�n�n����n�n�ւ̕ϊ��s��� ��ii �Ƃ���ƁA ��i �� ��ii ��i�@�C�@��j �� ��jj ��j
������̎�����̎��ɑ�������
�@�@�@��ii ��jj �sij��i��j �� �si j ��i��j
��i�A��j �͔C�ӂ�����
�@�@�@�si j �� ��ii ��jj �sij�@�i �s��̌`�ŕ\������� �si j �� ��t�s�� �j
�@�@�@�@�@�@���@�s�̓e���\���ł���B
���͂͌n�n�ł��n�n�ł�����������@�sij�� i��j �� �si j ��i��j
�n�n����n�n�ւ̕ϊ��s��� ��ii �Ƃ���ƁA ��i �� ��ii ��i�@�C�@��j �� ��jj ��j
������̎�����̎��ɑ�������
�@�@�@��ii ��jj �sij��i��j �� �si j ��i��j
��i�A��j �͔C�ӂ�����
�@�@�@�si j �� ��ii ��jj �sij�@�i �s��̌`�ŕ\������� �si j �� ��t�s�� �j
�@�@�@�@�@�@���@�s�̓e���\���ł���B
(2) �����e���\��
�������[�����g�͂Q�̃x�N�g����ϐ��Ƃ���i�O�C�Q�j�̂Q�K���ςȃe���\���ł���B�i�ؖ��͉��L�Q�Ɓj
�����e���\���� �h�A�h �̐����� �hij�A�ϐ��̃x�N�g���� �A
�A �Ƃ���B
�Ƃ���B
�@�@�@�hij �� �h( i �C
i �C j )�@�@�C�@
j )�@�@�C�@ �� �i ��1�C��2�C��3 �j�@�@�C�@
�� �i ��1�C��2�C��3 �j�@�@�C�@ �� �i ��1�C��2�C��3 �j
�� �i ��1�C��2�C��3 �j
�@�@�@�@�@�@�@�@�@�i���C�����P�`�R�@�P�F�����@�Q�F�����@�R�F�����j
�@�@�@�h ( �C
�C ) �� �h ( ��i
) �� �h ( ��i  i �C��j
i �C��j  j ) �� ��i ��j �h (
j ) �� ��i ��j �h (  i �C
i �C j ) �� �hij ��i ��j
j ) �� �hij ��i ��j
�hij ���t�^�Q�F�������[�����g���A�������ς��u �Ƃ�����
�@�@�@�hij�@��
�ϐ��̃x�N�g��  �A
�A �Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�@�@�@�j �� �hij ��i ��j�^�Q
�͍��̂̉�]�^���G�l���M�[�ƂȂ�B
 ������`��
������`��  ���i
���i 1�C
1�C 2�C
2�C 3�j ���A
3�j ���A �Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�@�@�@�ki �� �hij��j�@�C�@�k �� �ki i
i
�Ɗp�^���ʂ����܂�B�p�^���ʂ̑傫����
�@�@�@�b�k�b �� �i�k�E�k�j1/2 �� �i�k12�{�k22�{�k32�j1/2
�i �h ���e���\���ł��鎖�̏ؖ� �j
�����e���\���� �h�A�h �̐����� �hij�A�ϐ��̃x�N�g����
 �A
�A �Ƃ���B
�Ƃ���B�@�@�@�hij �� �h(
 i �C
i �C j )�@�@�C�@
j )�@�@�C�@ �� �i ��1�C��2�C��3 �j�@�@�C�@
�� �i ��1�C��2�C��3 �j�@�@�C�@ �� �i ��1�C��2�C��3 �j
�� �i ��1�C��2�C��3 �j�@�@�@�@�@�@�@�@�@�i���C�����P�`�R�@�P�F�����@�Q�F�����@�R�F�����j
�@�@�@�h (
 �C
�C ) �� �h ( ��i
) �� �h ( ��i  i �C��j
i �C��j  j ) �� ��i ��j �h (
j ) �� ��i ��j �h (  i �C
i �C j ) �� �hij ��i ��j
j ) �� �hij ��i ��j�@�@�@�hij�@��

 �A
�A �Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�Ɋp���x �����i��1�C��2�C��3�j ���w�肷����@�@�@�j �� �hij ��i ��j�^�Q
�͍��̂̉�]�^���G�l���M�[�ƂȂ�B
 ������`��
������`��  ���i
���i 1�C
1�C 2�C
2�C 3�j ���A
3�j ���A �Ɋp���x �����i��1�C��2�C��3�j ���w�肷���
�Ɋp���x �����i��1�C��2�C��3�j ���w�肷����@�@�@�ki �� �hij��j�@�C�@�k �� �ki
 i
i�Ɗp�^���ʂ����܂�B�p�^���ʂ̑傫����
�@�@�@�b�k�b �� �i�k�E�k�j1/2 �� �i�k12�{�k22�{�k32�j1/2
(1)�̈��̓e���\���̏ꍇ�ƑS�������ŁA�s���h�A���́����̂̉�]�^���G�l���M�[�ƒu��������B
�t�^�S�F�i�O�C�Q�j �e���\���̐����̕ϊ�
��̃x�N�g����ϐ��Ƃ���i�O�C�Q�j �e���\���̌n�r�ł̐����A�����������i �C
�C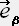 �j ����n�r�ł̐����A���� �� �� ���i
�j ����n�r�ł̐����A���� �� �� ���i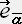 �C
�C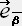 �j �ւ̕ϊ����͎����ɏ]���B
�j �ւ̕ϊ����͎����ɏ]���B
�@�@�@���� �� ��
 ������
������
�y�ؖ��z
��̕ϊ������s��ŕ\���ƁA������������ �ł���s��� �i���j �Ƃ���
�@�@�@�i���j �� �i���jT�i���j�i���j
�ƕ\�������o����B
�y�ؖ��z
 �C
�C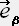 �j ����n�r�ł̐����A���� �� �� ���i
�j ����n�r�ł̐����A���� �� �� ���i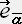 �C
�C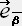 �j �ւ̕ϊ����͎����ɏ]���B
�j �ւ̕ϊ����͎����ɏ]���B�@�@�@���� �� ��

 ������
�������y�ؖ��z
��̕ϊ������s��ŕ\���ƁA������������ �ł���s��� �i���j �Ƃ���
�@�@�@�i���j �� �i���jT�i���j�i���j
�ƕ\�������o����B
�y�ؖ��z
�ϊ����̈ꕔ�A �������ɉ����āA����������i�����j��
�������ɉ����āA����������i�����j�� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j���o����B����
���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j���o����B����
�@�@�@�b���� �� ������ �� ������
������ �� ������  �� �i���j�i���j
�� �i���j�i���j
���� �� �� �b���� �ɉ����āA
�b���� �ɉ����āA ���s�i�����j�� �b���� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j������ɂ�
���s�i�����j�� �b���� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j������ɂ�  �̍s�Ɨ�����ւ����]�u�s��ɂ��Ȃ���Ȃ�Ȃ��B�]����
�̍s�Ɨ�����ւ����]�u�s��ɂ��Ȃ���Ȃ�Ȃ��B�]����
�@�@�@�i���j �� �i���jT�i���j�i���j
 �������ɉ����āA����������i�����j��
�������ɉ����āA����������i�����j�� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j���o����B����
���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j���o����B�����@�@�@�b���� ��
 ������ �� ������
������ �� ������  �� �i���j�i���j
�� �i���j�i���j���� �� ��
 �b���� �ɉ����āA
�b���� �ɉ����āA ���s�i�����j�� �b���� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j������ɂ�
���s�i�����j�� �b���� ���s�i�����j�Ɋւ��ă_�~�[�̓Y���Ȃ̂ōs�Z�i���|���Z�j������ɂ�  �̍s�Ɨ�����ւ����]�u�s��ɂ��Ȃ���Ȃ�Ȃ��B�]����
�̍s�Ɨ�����ւ����]�u�s��ɂ��Ȃ���Ȃ�Ȃ��B�]�����@�@�@�i���j �� �i���jT�i���j�i���j
 �y��
�y��  �ł��邩��
�ł��邩�� �C
�C �j ��
�j ��